Persistent Ballistic Entanglement Spreading with Optimal Control in Quantum Spin Chains

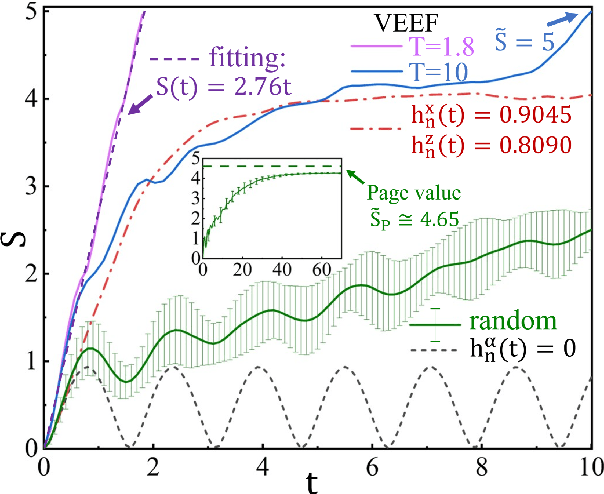
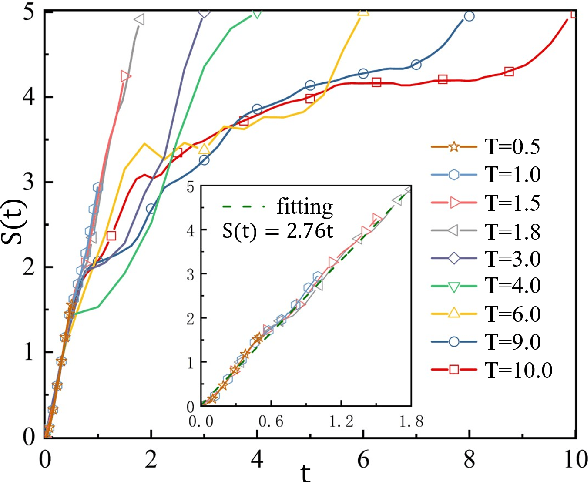
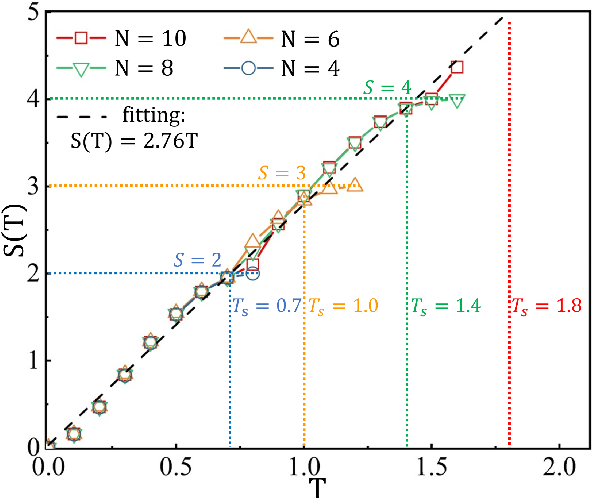
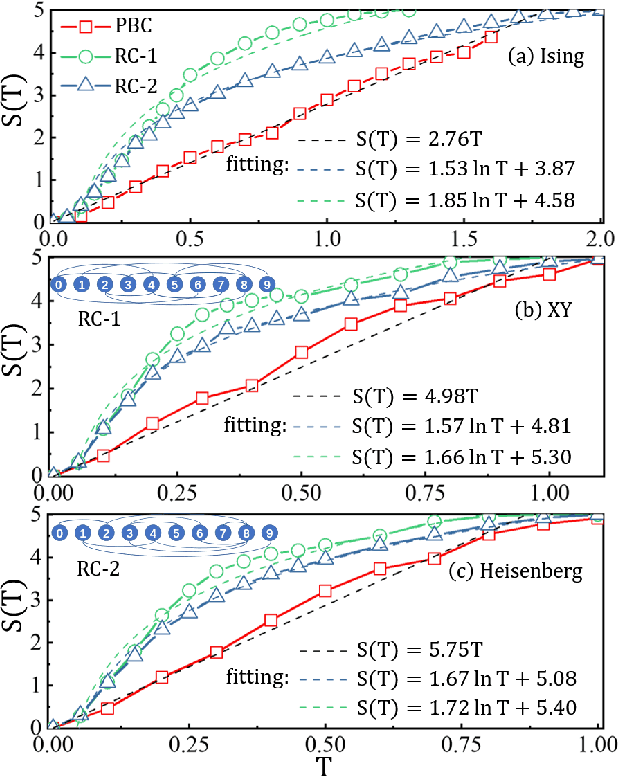
Entanglement propagation provides a key routine to understand quantum many-body dynamics in and out of equilibrium. In this work, we uncover that the ``variational entanglement-enhancing'' field (VEEF) robustly induces a persistent ballistic spreading of entanglement in quantum spin chains. The VEEF is time dependent, and is optimally controlled to maximize the bipartite entanglement entropy (EE) of the final state. Such a linear growth persists till the EE reaches the genuine saturation $\tilde{S} = - \log_{2} 2^{-\frac{N}{2}}=\frac{N}{2}$ with $N$ the total number of spins. The EE satisfies $S(t) = v t$ for the time $t \leq \frac{N}{2v}$, with $v$ the velocity. These results are in sharp contrast with the behaviors without VEEF, where the EE generally approaches a sub-saturation known as the Page value $\tilde{S}_{P} =\tilde{S} - \frac{1}{2\ln{2}}$ in the long-time limit, and the entanglement growth deviates from being linear before the Page value is reached. The dependence between the velocity and interactions is explored, with $v \simeq 2.76$, $4.98$, and $5.75$ for the spin chains with Ising, XY, and Heisenberg interactions, respectively. We further show that the nonlinear growth of EE emerges with the presence of long-range interactions.

Deep Machine Learning Reconstructing Lattice Topology with Strong Thermal Fluctuations

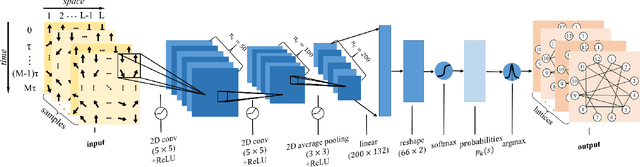
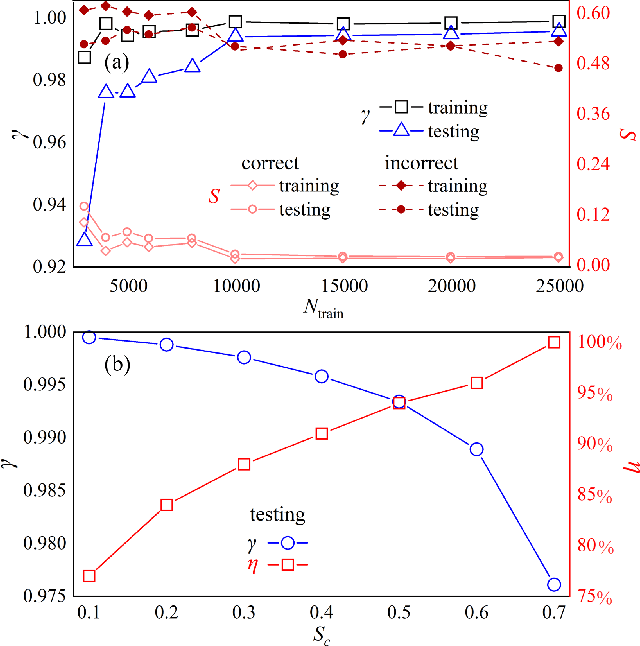
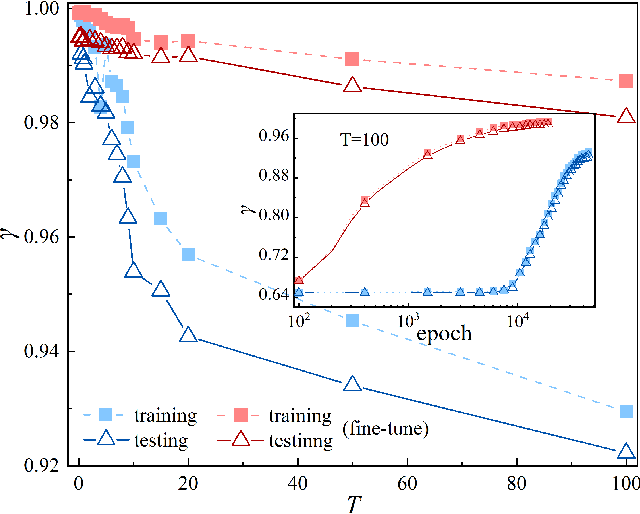
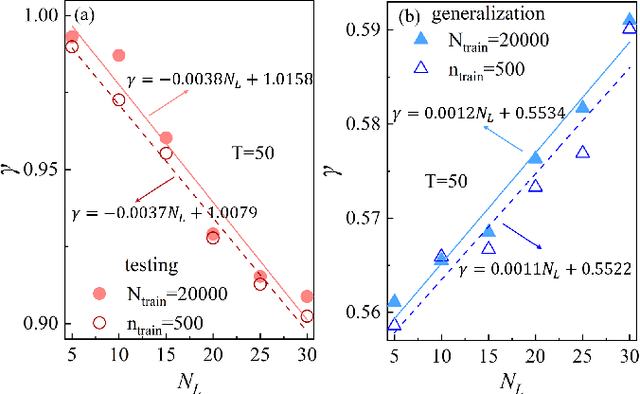
Applying artificial intelligence to scientific problems (namely AI for science) is currently under hot debate. However, the scientific problems differ much from the conventional ones with images, texts, and etc., where new challenges emerges with the unbalanced scientific data and complicated effects from the physical setups. In this work, we demonstrate the validity of the deep convolutional neural network (CNN) on reconstructing the lattice topology (i.e., spin connectivities) in the presence of strong thermal fluctuations and unbalanced data. Taking the kinetic Ising model with Glauber dynamics as an example, the CNN maps the time-dependent local magnetic momenta (a single-node feature) evolved from a specific initial configuration (dubbed as an evolution instance) to the probabilities of the presences of the possible couplings. Our scheme distinguishes from the previous ones that might require the knowledge on the node dynamics, the responses from perturbations, or the evaluations of statistic quantities such as correlations or transfer entropy from many evolution instances. The fine tuning avoids the "barren plateau" caused by the strong thermal fluctuations at high temperatures. Accurate reconstructions can be made where the thermal fluctuations dominate over the correlations and consequently the statistic methods in general fail. Meanwhile, we unveil the generalization of CNN on dealing with the instances evolved from the unlearnt initial spin configurations and those with the unlearnt lattices. We raise an open question on the learning with unbalanced data in the nearly "double-exponentially" large sample space.