Non-parametric Active Learning and Rate Reduction in Many-body Hilbert Space with Rescaled Logarithmic Fidelity

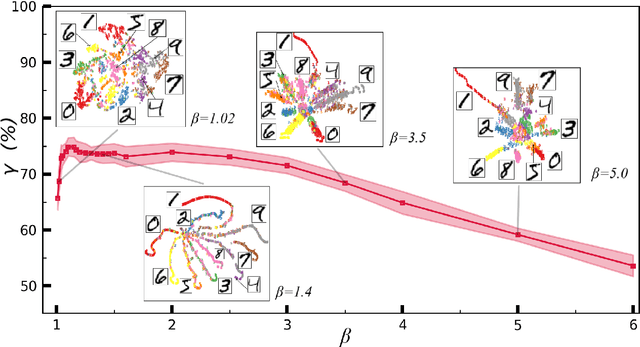
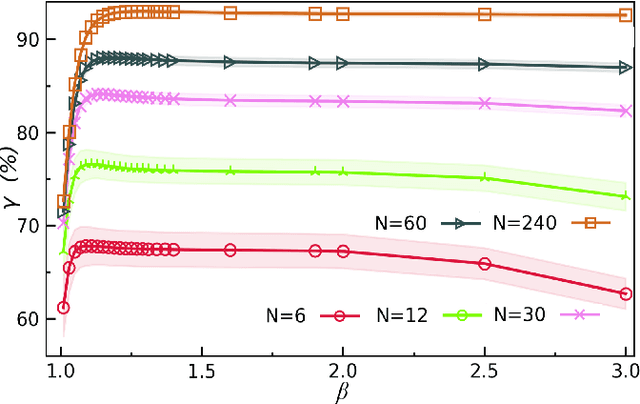
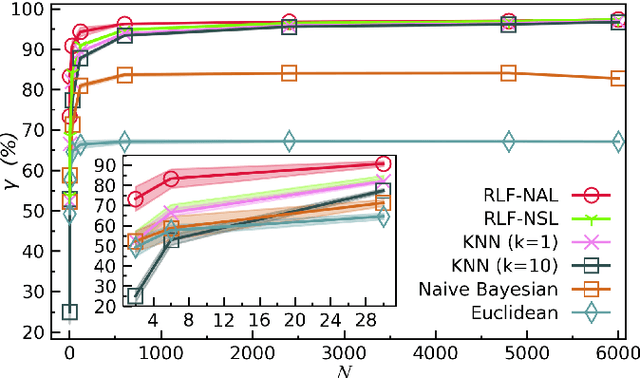
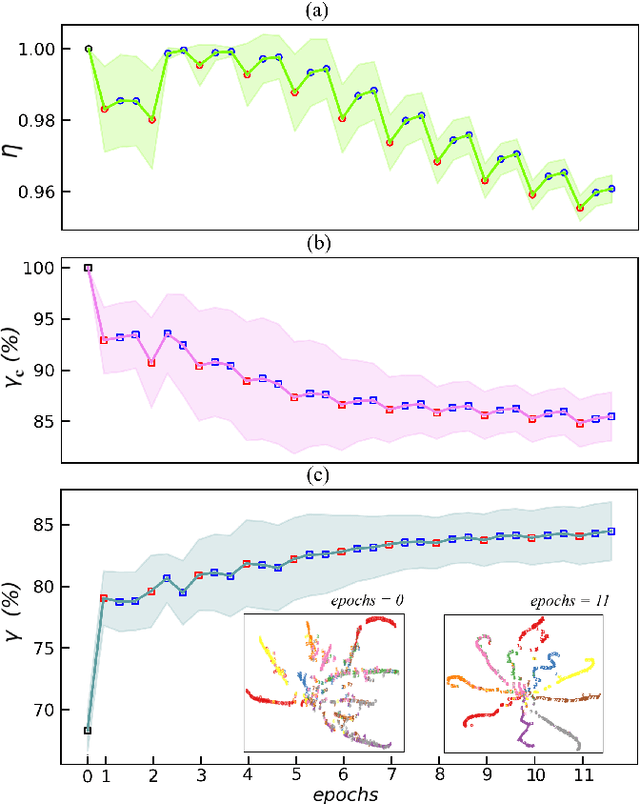
In quantum and quantum-inspired machine learning, the very first step is to embed the data in quantum space known as Hilbert space. Developing quantum kernel function (QKF), which defines the distances among the samples in the Hilbert space, belongs to the fundamental topics for machine learning. In this work, we propose the rescaled logarithmic fidelity (RLF) and a non-parametric active learning in the quantum space, which we name as RLF-NAL. The rescaling takes advantage of the non-linearity of the kernel to tune the mutual distances of samples in the Hilbert space, and meanwhile avoids the exponentially-small fidelities between quantum many-qubit states. We compare RLF-NAL with several well-known non-parametric algorithms including naive Bayes classifiers, $k$-nearest neighbors, and spectral clustering. Our method exhibits excellent accuracy particularly for the unsupervised case with no labeled samples and the few-shot cases with small numbers of labeled samples. With the visualizations by t-SNE, our results imply that the machine learning in the Hilbert space complies with the principles of maximal coding rate reduction, where the low-dimensional data exhibit within-class compressibility, between-class discrimination, and overall diversity. Our proposals can be applied to other quantum and quantum-inspired machine learning, including the methods using the parametric models such as tensor networks, quantum circuits, and quantum neural networks.