Entanglement-guided architectures of machine learning by quantum tensor network
Paper and Code
Jun 26, 2018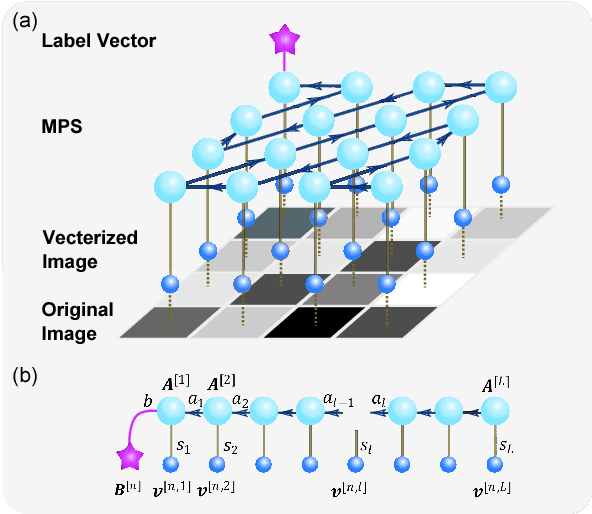
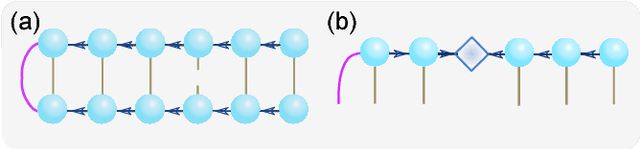
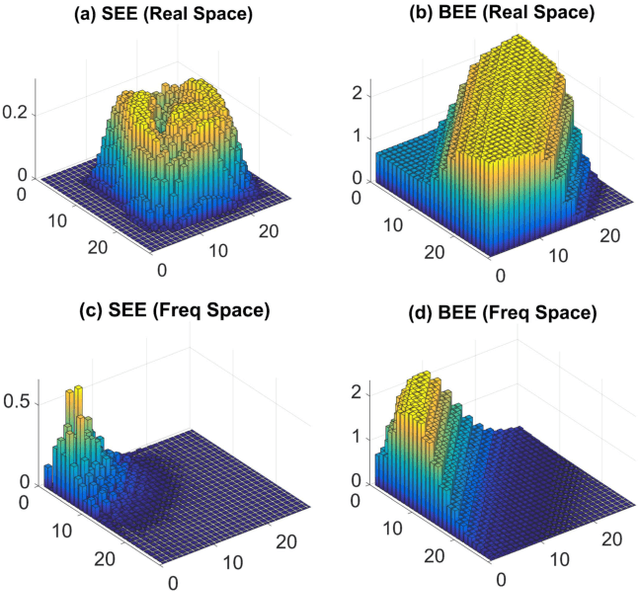
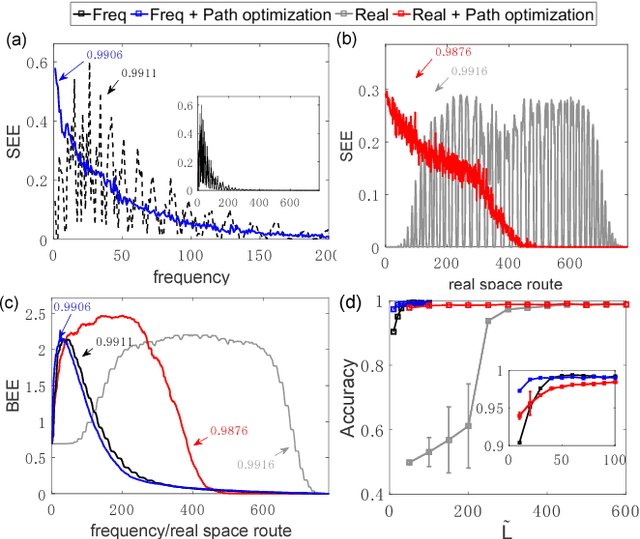
It is a fundamental, but still elusive question whether the schemes based on quantum mechanics, in particular on quantum entanglement, can be used for classical information processing and machine learning. Even partial answer to this question would bring important insights to both fields of machine learning and quantum mechanics. In this work, we implement simple numerical experiments, related to pattern/images classification, in which we represent the classifiers by many-qubit quantum states written in the matrix product states (MPS). Classical machine learning algorithm is applied to these quantum states to learn the classical data. We explicitly show how quantum entanglement (i.e., single-site and bipartite entanglement) can emerge in such represented images. Entanglement characterizes here the importance of data, and such information are practically used to guide the architecture of MPS, and improve the efficiency. The number of needed qubits can be reduced to less than 1/10 of the original number, which is within the access of the state-of-the-art quantum computers. We expect such numerical experiments could open new paths in charactering classical machine learning algorithms, and at the same time shed lights on the generic quantum simulations/computations of machine learning tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge