Preface: Characterisation of Physical Processes from Anomalous Diffusion Data

Preface to the special issue "Characterisation of Physical Processes from Anomalous Diffusion Data" associated with the Anomalous Diffusion Challenge ( https://andi-challenge.org ) and published in Journal of Physics A: Mathematical and Theoretical. The list of articles included in the special issue can be accessed at https://iopscience.iop.org/journal/1751-8121/page/Characterisation-of-Physical-Processes-from-Anomalous-Diffusion-Data .

Machine learning method for single trajectory characterization

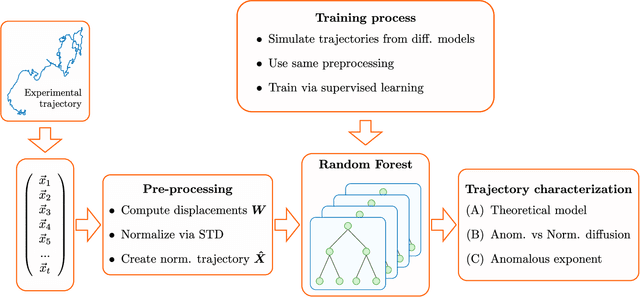
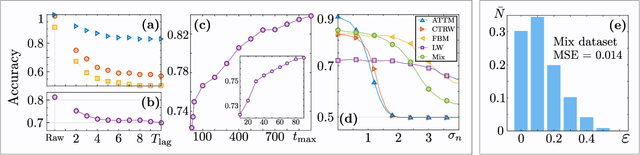
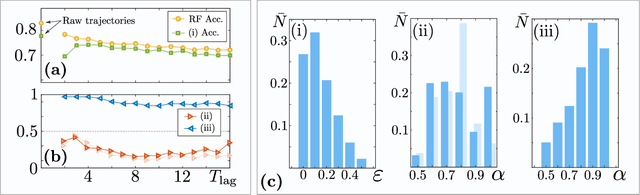
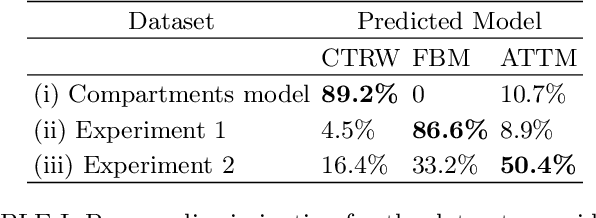
In order to study transport in complex environments, it is extremely important to determine the physical mechanism underlying diffusion, and precisely characterize its nature and parameters. Often, this task is strongly impacted by data consisting of trajectories with short length and limited localization precision. In this paper, we propose a machine learning method based on a random forest architecture, which is able to associate even very short trajectories to the underlying diffusion mechanism with a high accuracy. In addition, the method is able to classify the motion according to normal or anomalous diffusion, and determine its anomalous exponent with a small error. The method provides highly accurate outputs even when working with very short trajectories and in the presence of experimental noise. We further demonstrate the application of transfer learning to experimental and simulated data not included in the training/testing dataset. This allows for a full, high-accuracy characterization of experimental trajectories without the need of any prior information.