Global graph features unveiled by unsupervised geometric deep learning

Graphs provide a powerful framework for modeling complex systems, but their structural variability makes analysis and classification challenging. To address this, we introduce GAUDI (Graph Autoencoder Uncovering Descriptive Information), a novel unsupervised geometric deep learning framework that captures both local details and global structure. GAUDI employs an innovative hourglass architecture with hierarchical pooling and upsampling layers, linked through skip connections to preserve essential connectivity information throughout the encoding-decoding process. By mapping different realizations of a system - generated from the same underlying parameters - into a continuous, structured latent space, GAUDI disentangles invariant process-level features from stochastic noise. We demonstrate its power across multiple applications, including modeling small-world networks, characterizing protein assemblies from super-resolution microscopy, analyzing collective motion in the Vicsek model, and capturing age-related changes in brain connectivity. This approach not only improves the analysis of complex graphs but also provides new insights into emergent phenomena across diverse scientific domains.

Spatial Clustering of Molecular Localizations with Graph Neural Networks

Single-molecule localization microscopy generates point clouds corresponding to fluorophore localizations. Spatial cluster identification and analysis of these point clouds are crucial for extracting insights about molecular organization. However, this task becomes challenging in the presence of localization noise, high point density, or complex biological structures. Here, we introduce MIRO (Multimodal Integration through Relational Optimization), an algorithm that uses recurrent graph neural networks to transform the point clouds in order to improve clustering efficiency when applying conventional clustering techniques. We show that MIRO supports simultaneous processing of clusters of different shapes and at multiple scales, demonstrating improved performance across varied datasets. Our comprehensive evaluation demonstrates MIRO's transformative potential for single-molecule localization applications, showcasing its capability to revolutionize cluster analysis and provide accurate, reliable details of molecular architecture. In addition, MIRO's robust clustering capabilities hold promise for applications in various fields such as neuroscience, for the analysis of neural connectivity patterns, and environmental science, for studying spatial distributions of ecological data.

Learning minimal representations of stochastic processes with variational autoencoders

Stochastic processes have found numerous applications in science, as they are broadly used to model a variety of natural phenomena. Due to their intrinsic randomness and uncertainty, they are however difficult to characterize. Here, we introduce an unsupervised machine learning approach to determine the minimal set of parameters required to effectively describe the dynamics of a stochastic process. Our method builds upon an extended $\beta$-variational autoencoder architecture. By means of simulated datasets corresponding to paradigmatic diffusion models, we showcase its effectiveness in extracting the minimal relevant parameters that accurately describe these dynamics. Furthermore, the method enables the generation of new trajectories that faithfully replicate the expected stochastic behavior. Overall, our approach enables for the autonomous discovery of unknown parameters describing stochastic processes, hence enhancing our comprehension of complex phenomena across various fields.

Roadmap on Deep Learning for Microscopy

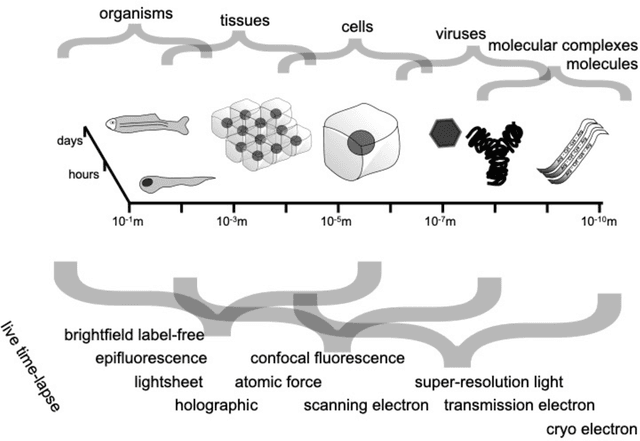
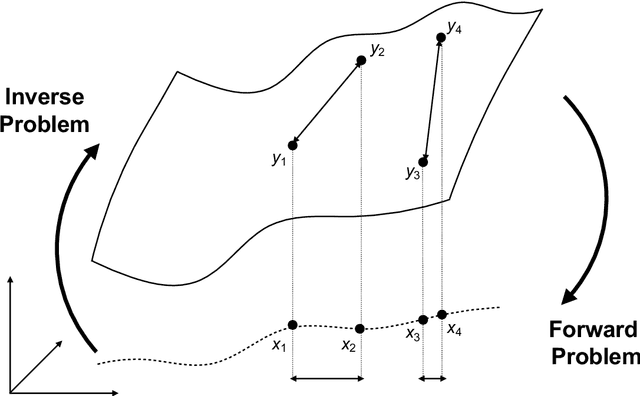
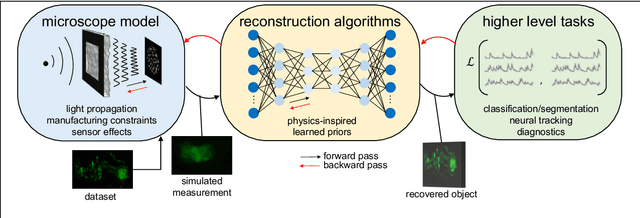
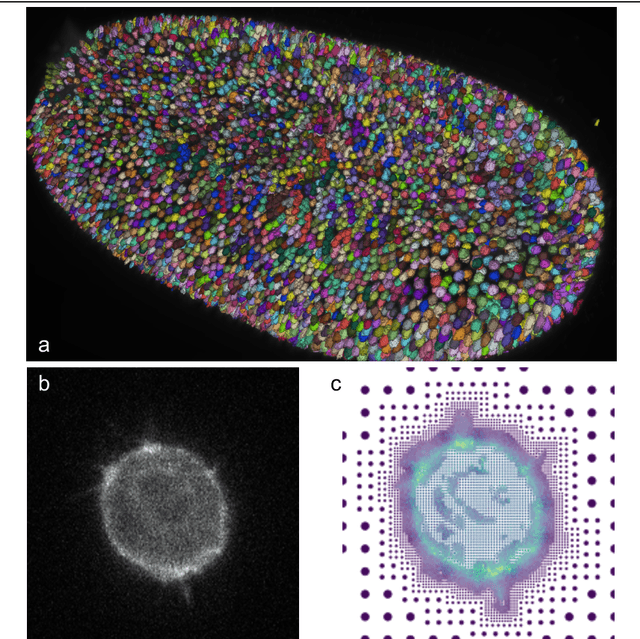
Through digital imaging, microscopy has evolved from primarily being a means for visual observation of life at the micro- and nano-scale, to a quantitative tool with ever-increasing resolution and throughput. Artificial intelligence, deep neural networks, and machine learning are all niche terms describing computational methods that have gained a pivotal role in microscopy-based research over the past decade. This Roadmap is written collectively by prominent researchers and encompasses selected aspects of how machine learning is applied to microscopy image data, with the aim of gaining scientific knowledge by improved image quality, automated detection, segmentation, classification and tracking of objects, and efficient merging of information from multiple imaging modalities. We aim to give the reader an overview of the key developments and an understanding of possibilities and limitations of machine learning for microscopy. It will be of interest to a wide cross-disciplinary audience in the physical sciences and life sciences.

Preface: Characterisation of Physical Processes from Anomalous Diffusion Data

Preface to the special issue "Characterisation of Physical Processes from Anomalous Diffusion Data" associated with the Anomalous Diffusion Challenge ( https://andi-challenge.org ) and published in Journal of Physics A: Mathematical and Theoretical. The list of articles included in the special issue can be accessed at https://iopscience.iop.org/journal/1751-8121/page/Characterisation-of-Physical-Processes-from-Anomalous-Diffusion-Data .

Geometric deep learning reveals the spatiotemporal fingerprint of microscopic motion

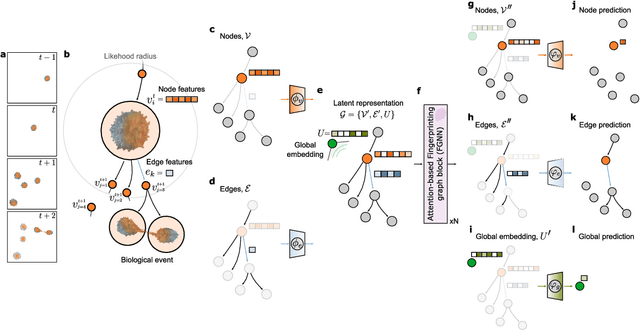
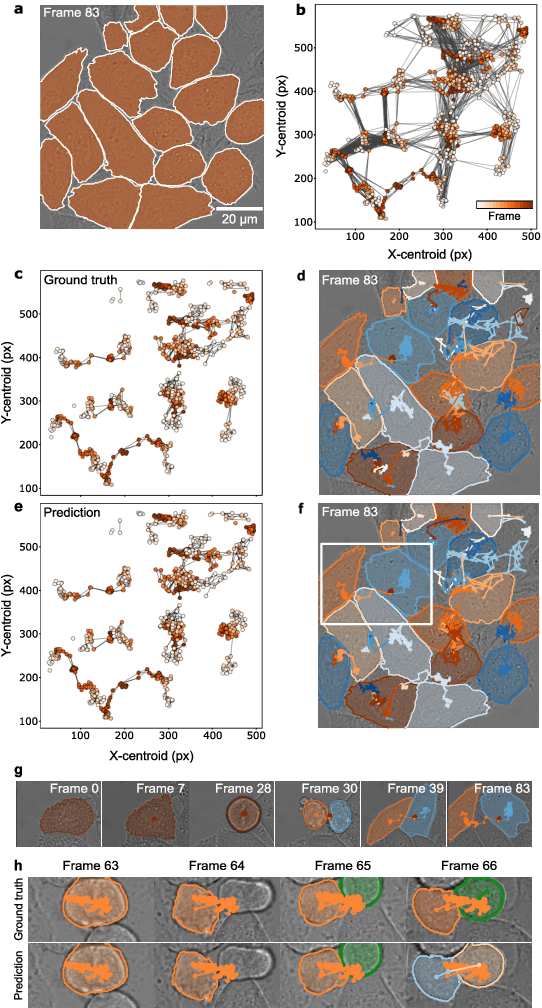
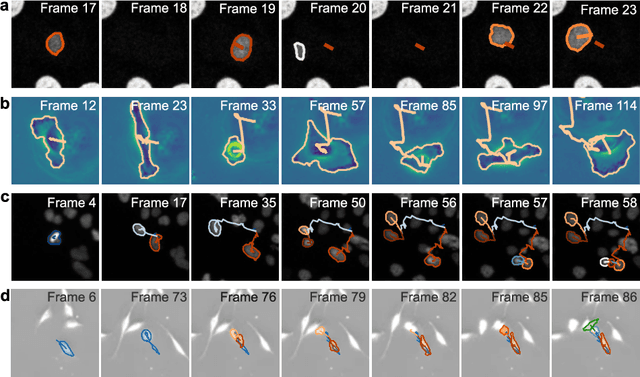
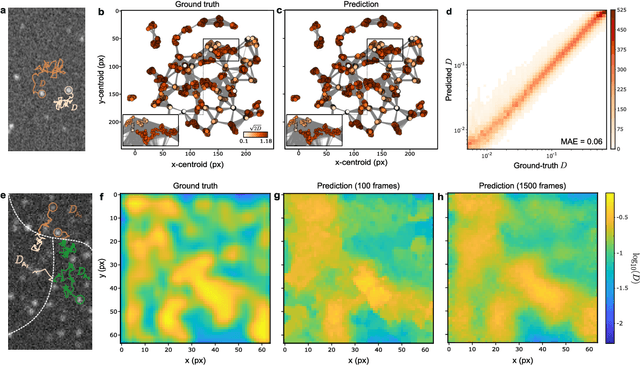
The characterization of dynamical processes in living systems provides important clues for their mechanistic interpretation and link to biological functions. Thanks to recent advances in microscopy techniques, it is now possible to routinely record the motion of cells, organelles, and individual molecules at multiple spatiotemporal scales in physiological conditions. However, the automated analysis of dynamics occurring in crowded and complex environments still lags behind the acquisition of microscopic image sequences. Here, we present a framework based on geometric deep learning that achieves the accurate estimation of dynamical properties in various biologically-relevant scenarios. This deep-learning approach relies on a graph neural network enhanced by attention-based components. By processing object features with geometric priors, the network is capable of performing multiple tasks, from linking coordinates into trajectories to inferring local and global dynamic properties. We demonstrate the flexibility and reliability of this approach by applying it to real and simulated data corresponding to a broad range of biological experiments.

Extreme Learning Machine for the Characterization of Anomalous Diffusion from Single Trajectories

The study of the dynamics of natural and artificial systems has provided several examples of deviations from Brownian behavior, generally defined as anomalous diffusion. The investigation of these dynamics can provide a better understanding of diffusing objects and their surrounding media, but a quantitative characterization from individual trajectories is often challenging. Efforts devoted to improving anomalous diffusion detection using classical statistics and machine learning have produced several new methods. Recently, the anomalous diffusion challenge (AnDi, https://www.andi-challenge.org) was launched to objectively assess these approaches on a common dataset, focusing on three aspects of anomalous diffusion: the inference of the anomalous diffusion exponent; the classification of the diffusion model; and the segmentation of trajectories. In this article, I describe a simple approach to tackle the tasks of the AnDi challenge by combining extreme learning machine and feature engineering (AnDi-ELM). The method reaches satisfactory performance while offering a straightforward implementation and fast training time with limited computing resources, making a suitable tool for fast preliminary screening.

Machine learning method for single trajectory characterization

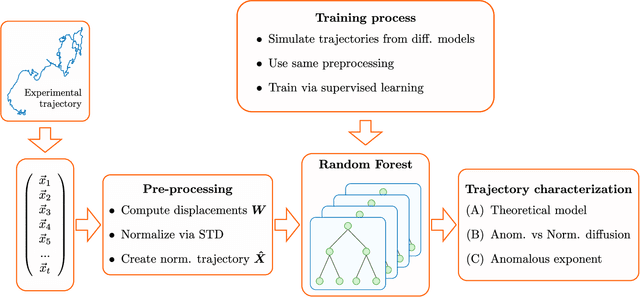
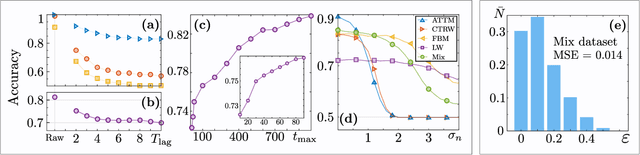
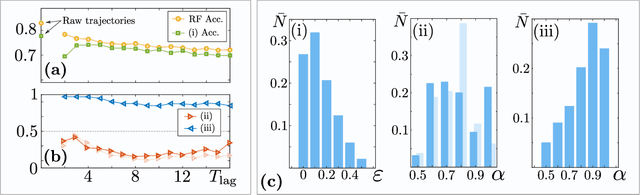
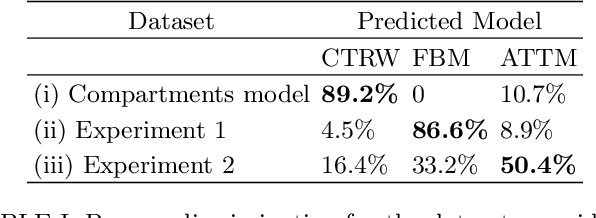
In order to study transport in complex environments, it is extremely important to determine the physical mechanism underlying diffusion, and precisely characterize its nature and parameters. Often, this task is strongly impacted by data consisting of trajectories with short length and limited localization precision. In this paper, we propose a machine learning method based on a random forest architecture, which is able to associate even very short trajectories to the underlying diffusion mechanism with a high accuracy. In addition, the method is able to classify the motion according to normal or anomalous diffusion, and determine its anomalous exponent with a small error. The method provides highly accurate outputs even when working with very short trajectories and in the presence of experimental noise. We further demonstrate the application of transfer learning to experimental and simulated data not included in the training/testing dataset. This allows for a full, high-accuracy characterization of experimental trajectories without the need of any prior information.