PMBO: Enhancing Black-Box Optimization through Multivariate Polynomial Surrogates

We introduce a surrogate-based black-box optimization method, termed Polynomial-model-based optimization (PMBO). The algorithm alternates polynomial approximation with Bayesian optimization steps, using Gaussian processes to model the error between the objective and its polynomial fit. We describe the algorithmic design of PMBO and compare the results of the performance of PMBO with several optimization methods for a set of analytic test functions. The results show that PMBO outperforms the classic Bayesian optimization and is robust with respect to the choice of its correlation function family and its hyper-parameter setting, which, on the contrary, need to be carefully tuned in classic Bayesian optimization. Remarkably, PMBO performs comparably with state-of-the-art evolutionary algorithms such as the Covariance Matrix Adaptation -- Evolution Strategy (CMA-ES). This finding suggests that PMBO emerges as the pivotal choice among surrogate-based optimization methods when addressing low-dimensional optimization problems. Hereby, the simple nature of polynomials opens the opportunity for interpretation and analysis of the inferred surrogate model, providing a macroscopic perspective on the landscape of the objective function.

Ensuring Topological Data-Structure Preservation under Autoencoder Compression due to Latent Space Regularization in Gauss--Legendre nodes

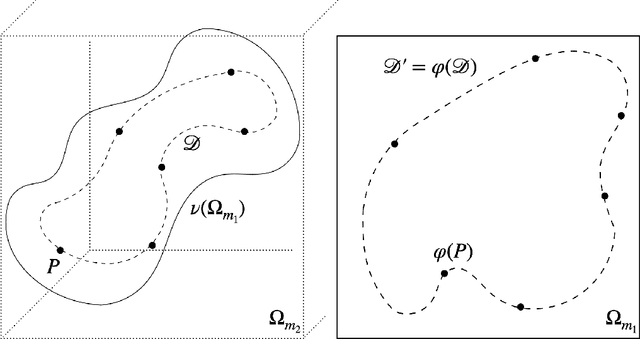
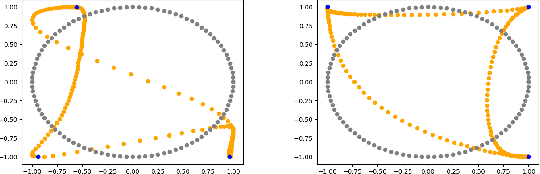
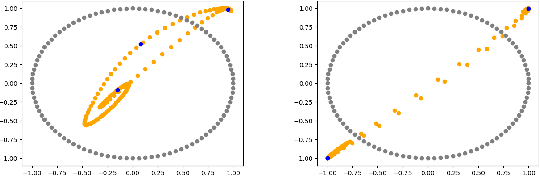
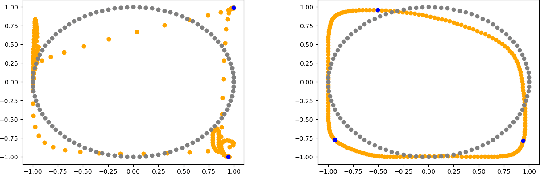
We formulate a data independent latent space regularisation constraint for general unsupervised autoencoders. The regularisation rests on sampling the autoencoder Jacobian in Legendre nodes, being the centre of the Gauss-Legendre quadrature. Revisiting this classic enables to prove that regularised autoencoders ensure a one-to-one re-embedding of the initial data manifold to its latent representation. Demonstrations show that prior proposed regularisation strategies, such as contractive autoencoding, cause topological defects already for simple examples, and so do convolutional based (variational) autoencoders. In contrast, topological preservation is ensured already by standard multilayer perceptron neural networks when being regularised due to our contribution. This observation extends through the classic FashionMNIST dataset up to real world encoding problems for MRI brain scans, suggesting that, across disciplines, reliable low dimensional representations of complex high-dimensional datasets can be delivered due to this regularisation technique.

Polynomial-Model-Based Optimization for Blackbox Objectives

For a wide range of applications the structure of systems like Neural Networks or complex simulations, is unknown and approximation is costly or even impossible. Black-box optimization seeks to find optimal (hyper-) parameters for these systems such that a pre-defined objective function is minimized. Polynomial-Model-Based Optimization (PMBO) is a novel blackbox optimizer that finds the minimum by fitting a polynomial surrogate to the objective function. Motivated by Bayesian optimization the model is iteratively updated according to the acquisition function Expected Improvement, thus balancing the exploitation and exploration rate and providing an uncertainty estimate of the model. PMBO is benchmarked against other state-of-the-art algorithms for a given set of artificial, analytical functions. PMBO competes successfully with those algorithms and even outperforms all of them in some cases. As the results suggest, we believe PMBO is the pivotal choice for solving blackbox optimization tasks occurring in a wide range of disciplines.

Roadmap on Deep Learning for Microscopy

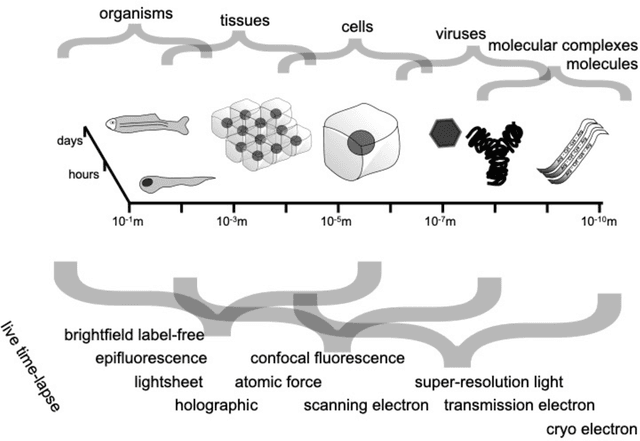
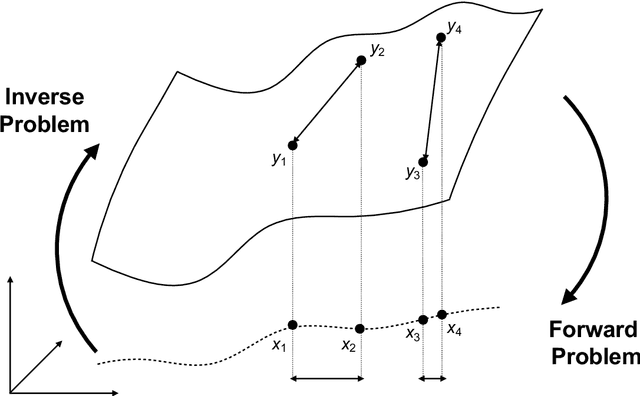
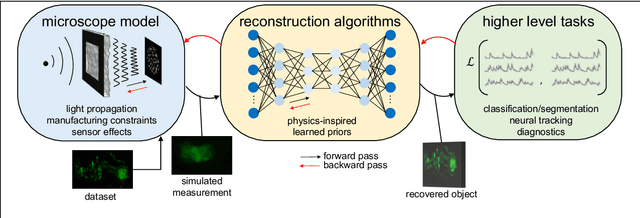
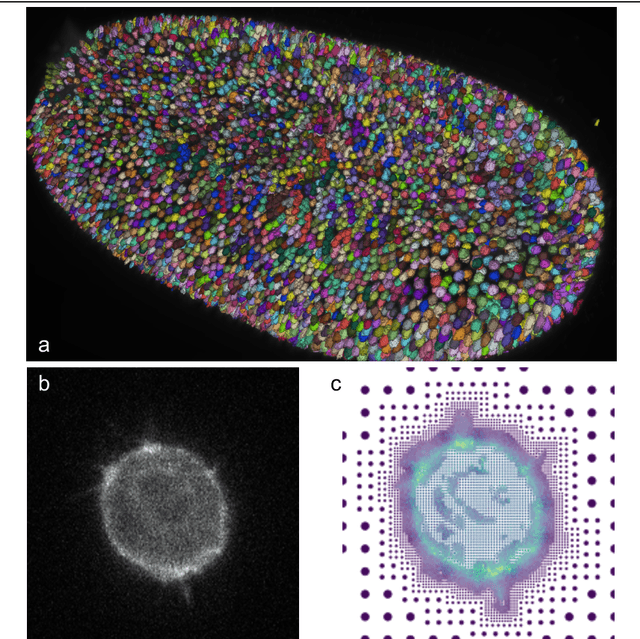
Through digital imaging, microscopy has evolved from primarily being a means for visual observation of life at the micro- and nano-scale, to a quantitative tool with ever-increasing resolution and throughput. Artificial intelligence, deep neural networks, and machine learning are all niche terms describing computational methods that have gained a pivotal role in microscopy-based research over the past decade. This Roadmap is written collectively by prominent researchers and encompasses selected aspects of how machine learning is applied to microscopy image data, with the aim of gaining scientific knowledge by improved image quality, automated detection, segmentation, classification and tracking of objects, and efficient merging of information from multiple imaging modalities. We aim to give the reader an overview of the key developments and an understanding of possibilities and limitations of machine learning for microscopy. It will be of interest to a wide cross-disciplinary audience in the physical sciences and life sciences.

Learning Partial Differential Equations by Spectral Approximates of General Sobolev Spaces

We introduce a novel spectral, finite-dimensional approximation of general Sobolev spaces in terms of Chebyshev polynomials. Based on this polynomial surrogate model (PSM), we realise a variational formulation, solving a vast class of linear and non-linear partial differential equations (PDEs). The PSMs are as flexible as the physics-informed neural nets (PINNs) and provide an alternative for addressing inverse PDE problems, such as PDE-parameter inference. In contrast to PINNs, the PSMs result in a convex optimisation problem for a vast class of PDEs, including all linear ones, in which case the PSM-approximate is efficiently computable due to the exponential convergence rate of the underlying variational gradient descent. As a practical consequence prominent PDE problems were resolved by the PSMs without High Performance Computing (HPC) on a local machine. This gain in efficiency is complemented by an increase of approximation power, outperforming PINN alternatives in both accuracy and runtime. Beyond the empirical evidence we give here, the translation of classic PDE theory in terms of the Sobolev space approximates suggests the PSMs to be universally applicable to well-posed, regular forward and inverse PDE problems.

Replacing Automatic Differentiation by Sobolev Cubatures fastens Physics Informed Neural Nets and strengthens their Approximation Power

We present a novel class of approximations for variational losses, being applicable for the training of physics-informed neural nets (PINNs). The loss formulation reflects classic Sobolev space theory for partial differential equations and their weak formulations. The loss computation rests on an extension of Gauss-Legendre cubatures, we term Sobolev cubatures, replacing automatic differentiation (A.D.). We prove the runtime complexity of training the resulting Soblev-PINNs (SC-PINNs) to be less than required by PINNs relying on A.D. On top of one-to-two order of magnitude speed-up the SC-PINNs are demonstrated to achieve closer solution approximations for prominent forward and inverse PDE problems than established PINNs achieve.

InFlow: Robust outlier detection utilizing Normalizing Flows

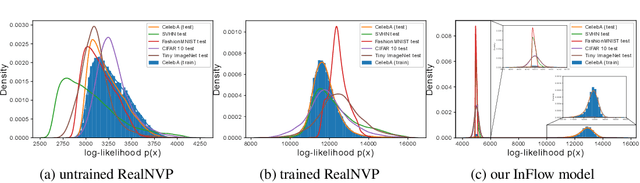
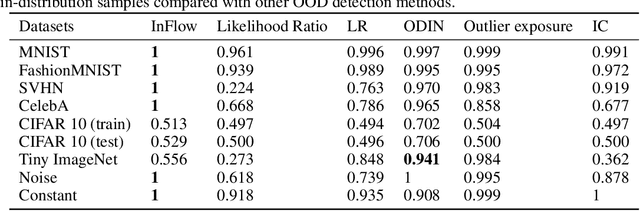
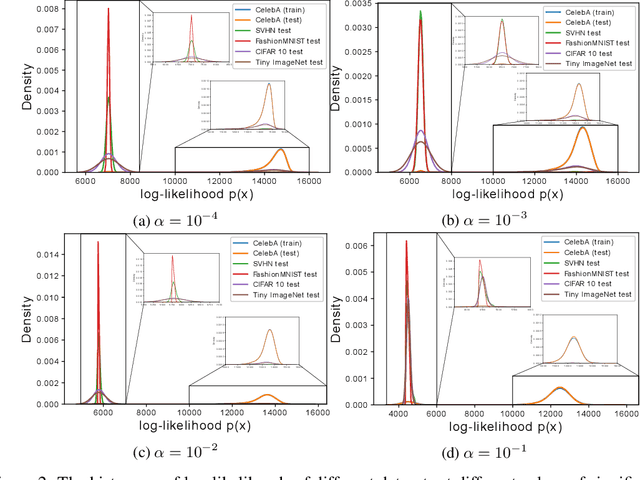
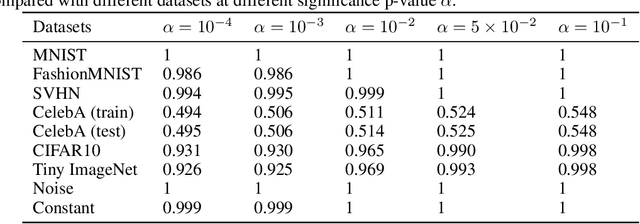
Normalizing flows are prominent deep generative models that provide tractable probability distributions and efficient density estimation. However, they are well known to fail while detecting Out-of-Distribution (OOD) inputs as they directly encode the local features of the input representations in their latent space. In this paper, we solve this overconfidence issue of normalizing flows by demonstrating that flows, if extended by an attention mechanism, can reliably detect outliers including adversarial attacks. Our approach does not require outlier data for training and we showcase the efficiency of our method for OOD detection by reporting state-of-the-art performance in diverse experimental settings. Code available at https://github.com/ComputationalRadiationPhysics/InFlow .