PMBO: Enhancing Black-Box Optimization through Multivariate Polynomial Surrogates

We introduce a surrogate-based black-box optimization method, termed Polynomial-model-based optimization (PMBO). The algorithm alternates polynomial approximation with Bayesian optimization steps, using Gaussian processes to model the error between the objective and its polynomial fit. We describe the algorithmic design of PMBO and compare the results of the performance of PMBO with several optimization methods for a set of analytic test functions. The results show that PMBO outperforms the classic Bayesian optimization and is robust with respect to the choice of its correlation function family and its hyper-parameter setting, which, on the contrary, need to be carefully tuned in classic Bayesian optimization. Remarkably, PMBO performs comparably with state-of-the-art evolutionary algorithms such as the Covariance Matrix Adaptation -- Evolution Strategy (CMA-ES). This finding suggests that PMBO emerges as the pivotal choice among surrogate-based optimization methods when addressing low-dimensional optimization problems. Hereby, the simple nature of polynomials opens the opportunity for interpretation and analysis of the inferred surrogate model, providing a macroscopic perspective on the landscape of the objective function.

Diffeomorphic Measure Matching with Kernels for Generative Modeling

This article presents a general framework for the transport of probability measures towards minimum divergence generative modeling and sampling using ordinary differential equations (ODEs) and Reproducing Kernel Hilbert Spaces (RKHSs), inspired by ideas from diffeomorphic matching and image registration. A theoretical analysis of the proposed method is presented, giving a priori error bounds in terms of the complexity of the model, the number of samples in the training set, and model misspecification. An extensive suite of numerical experiments further highlights the properties, strengths, and weaknesses of the method and extends its applicability to other tasks, such as conditional simulation and inference.

Computational Hypergraph Discovery, a Gaussian Process framework for connecting the dots

Most scientific challenges can be framed into one of the following three levels of complexity of function approximation. Type 1: Approximate an unknown function given input/output data. Type 2: Consider a collection of variables and functions, some of which are unknown, indexed by the nodes and hyperedges of a hypergraph (a generalized graph where edges can connect more than two vertices). Given partial observations of the variables of the hypergraph (satisfying the functional dependencies imposed by its structure), approximate all the unobserved variables and unknown functions. Type 3: Expanding on Type 2, if the hypergraph structure itself is unknown, use partial observations of the variables of the hypergraph to discover its structure and approximate its unknown functions. While most Computational Science and Engineering and Scientific Machine Learning challenges can be framed as Type 1 and Type 2 problems, many scientific problems can only be categorized as Type 3. Despite their prevalence, these Type 3 challenges have been largely overlooked due to their inherent complexity. Although Gaussian Process (GP) methods are sometimes perceived as well-founded but old technology limited to Type 1 curve fitting, their scope has recently been expanded to Type 2 problems. In this paper, we introduce an interpretable GP framework for Type 3 problems, targeting the data-driven discovery and completion of computational hypergraphs. Our approach is based on a kernel generalization of Row Echelon Form reduction from linear systems to nonlinear ones and variance-based analysis. Here, variables are linked via GPs and those contributing to the highest data variance unveil the hypergraph's structure. We illustrate the scope and efficiency of the proposed approach with applications to (algebraic) equation discovery, network discovery (gene pathways, chemical, and mechanical) and raw data analysis.

Error Analysis of Kernel/GP Methods for Nonlinear and Parametric PDEs

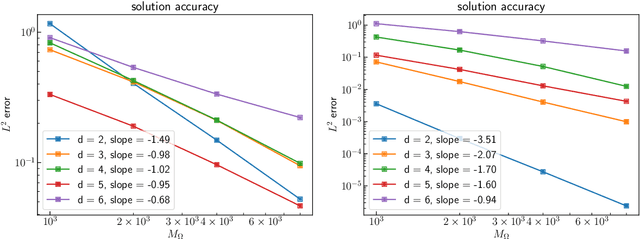
We introduce a priori Sobolev-space error estimates for the solution of nonlinear, and possibly parametric, PDEs using Gaussian process and kernel based methods. The primary assumptions are: (1) a continuous embedding of the reproducing kernel Hilbert space of the kernel into a Sobolev space of sufficient regularity; and (2) the stability of the differential operator and the solution map of the PDE between corresponding Sobolev spaces. The proof is articulated around Sobolev norm error estimates for kernel interpolants and relies on the minimizing norm property of the solution. The error estimates demonstrate dimension-benign convergence rates if the solution space of the PDE is smooth enough. We illustrate these points with applications to high-dimensional nonlinear elliptic PDEs and parametric PDEs. Although some recent machine learning methods have been presented as breaking the curse of dimensionality in solving high-dimensional PDEs, our analysis suggests a more nuanced picture: there is a trade-off between the regularity of the solution and the presence of the curse of dimensionality. Therefore, our results are in line with the understanding that the curse is absent when the solution is regular enough.

Kernel Methods are Competitive for Operator Learning

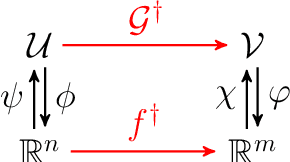
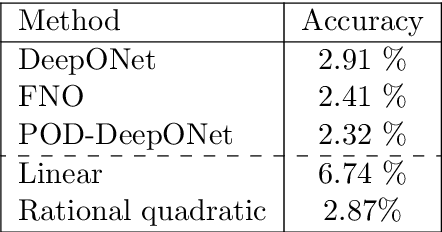
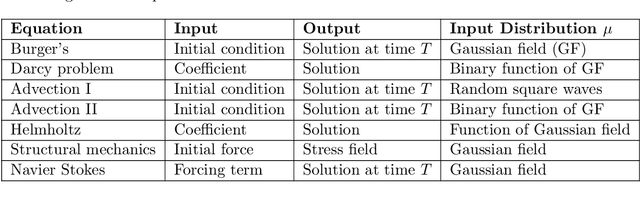
We present a general kernel-based framework for learning operators between Banach spaces along with a priori error analysis and comprehensive numerical comparisons with popular neural net (NN) approaches such as Deep Operator Net (DeepONet) [Lu et al.] and Fourier Neural Operator (FNO) [Li et al.]. We consider the setting where the input/output spaces of target operator $\mathcal{G}^\dagger\,:\, \mathcal{U}\to \mathcal{V}$ are reproducing kernel Hilbert spaces (RKHS), the data comes in the form of partial observations $\phi(u_i), \varphi(v_i)$ of input/output functions $v_i=\mathcal{G}^\dagger(u_i)$ ($i=1,\ldots,N$), and the measurement operators $\phi\,:\, \mathcal{U}\to \mathbb{R}^n$ and $\varphi\,:\, \mathcal{V} \to \mathbb{R}^m$ are linear. Writing $\psi\,:\, \mathbb{R}^n \to \mathcal{U}$ and $\chi\,:\, \mathbb{R}^m \to \mathcal{V}$ for the optimal recovery maps associated with $\phi$ and $\varphi$, we approximate $\mathcal{G}^\dagger$ with $\bar{\mathcal{G}}=\chi \circ \bar{f} \circ \phi$ where $\bar{f}$ is an optimal recovery approximation of $f^\dagger:=\varphi \circ \mathcal{G}^\dagger \circ \psi\,:\,\mathbb{R}^n \to \mathbb{R}^m$. We show that, even when using vanilla kernels (e.g., linear or Mat\'{e}rn), our approach is competitive in terms of cost-accuracy trade-off and either matches or beats the performance of NN methods on a majority of benchmarks. Additionally, our framework offers several advantages inherited from kernel methods: simplicity, interpretability, convergence guarantees, a priori error estimates, and Bayesian uncertainty quantification. As such, it can serve as a natural benchmark for operator learning.

Multiclass classification utilising an estimated algorithmic probability prior

Methods of pattern recognition and machine learning are applied extensively in science, technology, and society. Hence, any advances in related theory may translate into large-scale impact. Here we explore how algorithmic information theory, especially algorithmic probability, may aid in a machine learning task. We study a multiclass supervised classification problem, namely learning the RNA molecule sequence-to-shape map, where the different possible shapes are taken to be the classes. The primary motivation for this work is a proof of concept example, where a concrete, well-motivated machine learning task can be aided by approximations to algorithmic probability. Our approach is based on directly estimating the class (i.e., shape) probabilities from shape complexities, and using the estimated probabilities as a prior in a Gaussian process learning problem. Naturally, with a large amount of training data, the prior has no significant influence on classification accuracy, but in the very small training data regime, we show that using the prior can substantially improve classification accuracy. To our knowledge, this work is one of the first to demonstrate how algorithmic probability can aid in a concrete, real-world, machine learning problem.

Learning grounded word meaning representations on similarity graphs

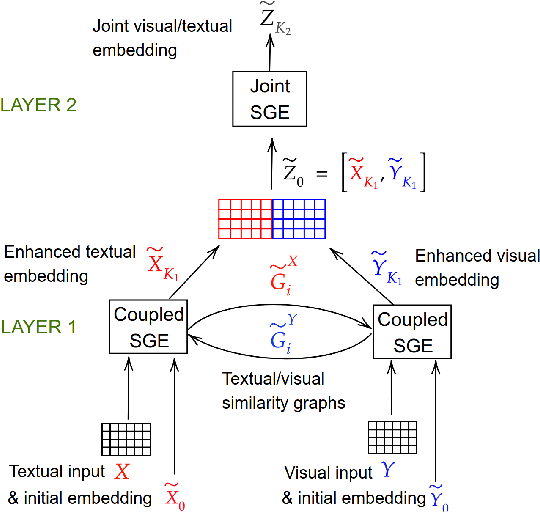
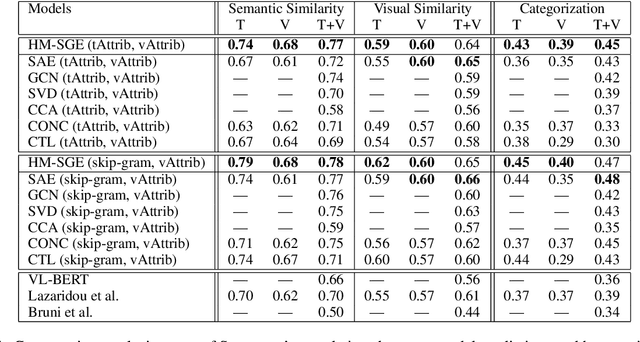
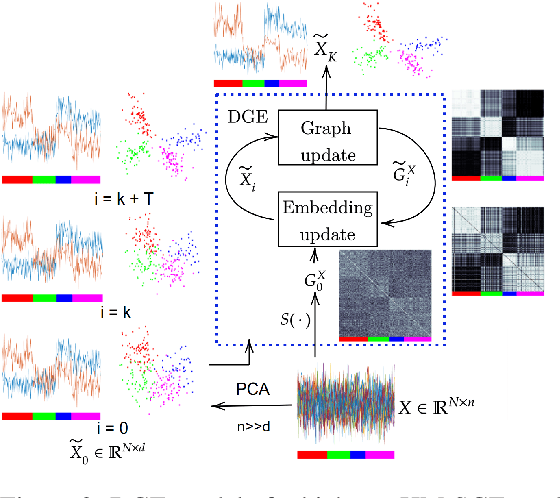
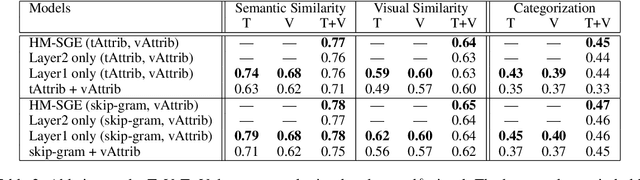
This paper introduces a novel approach to learn visually grounded meaning representations of words as low-dimensional node embeddings on an underlying graph hierarchy. The lower level of the hierarchy models modality-specific word representations through dedicated but communicating graphs, while the higher level puts these representations together on a single graph to learn a representation jointly from both modalities. The topology of each graph models similarity relations among words, and is estimated jointly with the graph embedding. The assumption underlying this model is that words sharing similar meaning correspond to communities in an underlying similarity graph in a low-dimensional space. We named this model Hierarchical Multi-Modal Similarity Graph Embedding (HM-SGE). Experimental results validate the ability of HM-SGE to simulate human similarity judgements and concept categorization, outperforming the state of the art.