Model aggregation: minimizing empirical variance outperforms minimizing empirical error

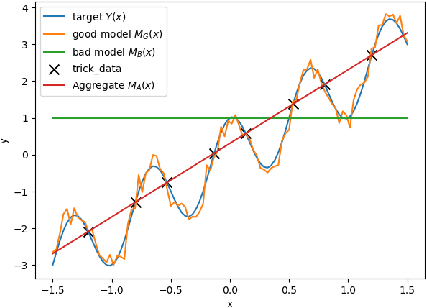
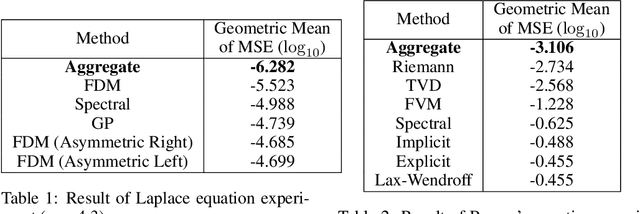
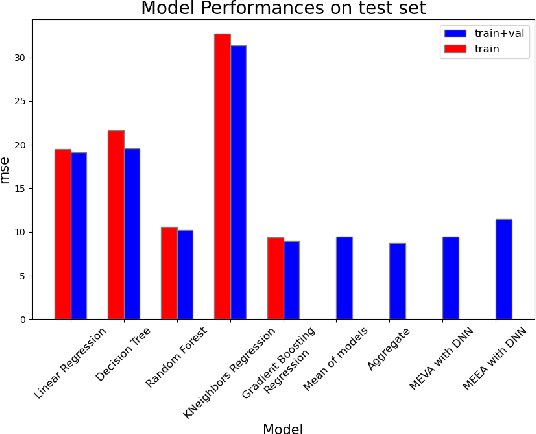
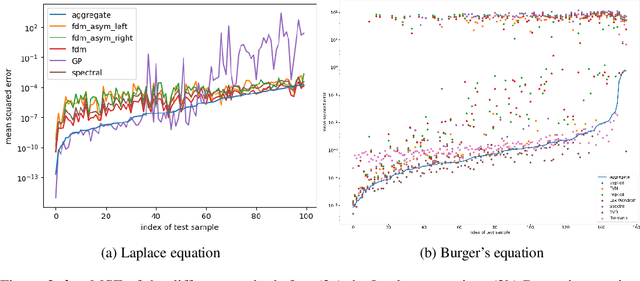
Whether deterministic or stochastic, models can be viewed as functions designed to approximate a specific quantity of interest. We propose a data-driven framework that aggregates predictions from diverse models into a single, more accurate output. This aggregation approach exploits each model's strengths to enhance overall accuracy. It is non-intrusive - treating models as black-box functions - model-agnostic, requires minimal assumptions, and can combine outputs from a wide range of models, including those from machine learning and numerical solvers. We argue that the aggregation process should be point-wise linear and propose two methods to find an optimal aggregate: Minimal Error Aggregation (MEA), which minimizes the aggregate's prediction error, and Minimal Variance Aggregation (MVA), which minimizes its variance. While MEA is inherently more accurate when correlations between models and the target quantity are perfectly known, Minimal Empirical Variance Aggregation (MEVA), an empirical version of MVA - consistently outperforms Minimal Empirical Error Aggregation (MEEA), the empirical counterpart of MEA, when these correlations must be estimated from data. The key difference is that MEVA constructs an aggregate by estimating model errors, while MEEA treats the models as features for direct interpolation of the quantity of interest. This makes MEEA more susceptible to overfitting and poor generalization, where the aggregate may underperform individual models during testing. We demonstrate the versatility and effectiveness of our framework in various applications, such as data science and partial differential equations, showing how it successfully integrates traditional solvers with machine learning models to improve both robustness and accuracy.

Computational Hypergraph Discovery, a Gaussian Process framework for connecting the dots

Most scientific challenges can be framed into one of the following three levels of complexity of function approximation. Type 1: Approximate an unknown function given input/output data. Type 2: Consider a collection of variables and functions, some of which are unknown, indexed by the nodes and hyperedges of a hypergraph (a generalized graph where edges can connect more than two vertices). Given partial observations of the variables of the hypergraph (satisfying the functional dependencies imposed by its structure), approximate all the unobserved variables and unknown functions. Type 3: Expanding on Type 2, if the hypergraph structure itself is unknown, use partial observations of the variables of the hypergraph to discover its structure and approximate its unknown functions. While most Computational Science and Engineering and Scientific Machine Learning challenges can be framed as Type 1 and Type 2 problems, many scientific problems can only be categorized as Type 3. Despite their prevalence, these Type 3 challenges have been largely overlooked due to their inherent complexity. Although Gaussian Process (GP) methods are sometimes perceived as well-founded but old technology limited to Type 1 curve fitting, their scope has recently been expanded to Type 2 problems. In this paper, we introduce an interpretable GP framework for Type 3 problems, targeting the data-driven discovery and completion of computational hypergraphs. Our approach is based on a kernel generalization of Row Echelon Form reduction from linear systems to nonlinear ones and variance-based analysis. Here, variables are linked via GPs and those contributing to the highest data variance unveil the hypergraph's structure. We illustrate the scope and efficiency of the proposed approach with applications to (algebraic) equation discovery, network discovery (gene pathways, chemical, and mechanical) and raw data analysis.