Kernel Methods are Competitive for Operator Learning
Paper and Code
Apr 26, 2023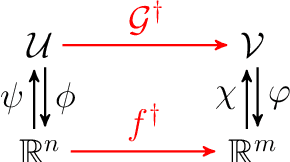
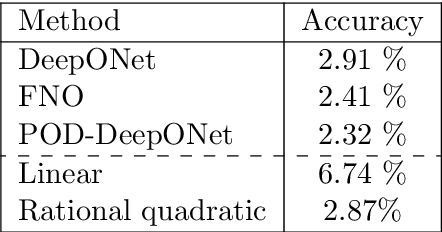

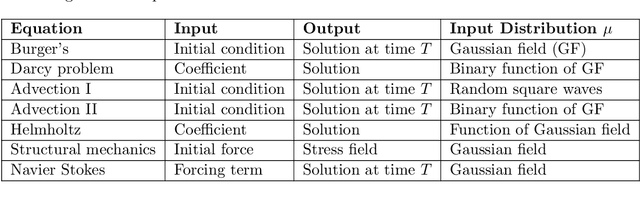
We present a general kernel-based framework for learning operators between Banach spaces along with a priori error analysis and comprehensive numerical comparisons with popular neural net (NN) approaches such as Deep Operator Net (DeepONet) [Lu et al.] and Fourier Neural Operator (FNO) [Li et al.]. We consider the setting where the input/output spaces of target operator $\mathcal{G}^\dagger\,:\, \mathcal{U}\to \mathcal{V}$ are reproducing kernel Hilbert spaces (RKHS), the data comes in the form of partial observations $\phi(u_i), \varphi(v_i)$ of input/output functions $v_i=\mathcal{G}^\dagger(u_i)$ ($i=1,\ldots,N$), and the measurement operators $\phi\,:\, \mathcal{U}\to \mathbb{R}^n$ and $\varphi\,:\, \mathcal{V} \to \mathbb{R}^m$ are linear. Writing $\psi\,:\, \mathbb{R}^n \to \mathcal{U}$ and $\chi\,:\, \mathbb{R}^m \to \mathcal{V}$ for the optimal recovery maps associated with $\phi$ and $\varphi$, we approximate $\mathcal{G}^\dagger$ with $\bar{\mathcal{G}}=\chi \circ \bar{f} \circ \phi$ where $\bar{f}$ is an optimal recovery approximation of $f^\dagger:=\varphi \circ \mathcal{G}^\dagger \circ \psi\,:\,\mathbb{R}^n \to \mathbb{R}^m$. We show that, even when using vanilla kernels (e.g., linear or Mat\'{e}rn), our approach is competitive in terms of cost-accuracy trade-off and either matches or beats the performance of NN methods on a majority of benchmarks. Additionally, our framework offers several advantages inherited from kernel methods: simplicity, interpretability, convergence guarantees, a priori error estimates, and Bayesian uncertainty quantification. As such, it can serve as a natural benchmark for operator learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge