A spectral clustering-type algorithm for the consistent estimation of the Hurst distribution in moderately high dimensions

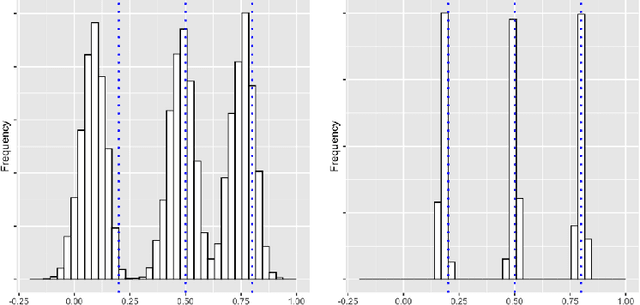
Scale invariance (fractality) is a prominent feature of the large-scale behavior of many stochastic systems. In this work, we construct an algorithm for the statistical identification of the Hurst distribution (in particular, the scaling exponents) undergirding a high-dimensional fractal system. The algorithm is based on wavelet random matrices, modified spectral clustering and a model selection step for picking the value of the clustering precision hyperparameter. In a moderately high-dimensional regime where the dimension, the sample size and the scale go to infinity, we show that the algorithm consistently estimates the Hurst distribution. Monte Carlo simulations show that the proposed methodology is efficient for realistic sample sizes and outperforms another popular clustering method based on mixed-Gaussian modeling. We apply the algorithm in the analysis of real-world macroeconomic time series to unveil evidence for cointegration.

Bayesian Multifractal Image Segmentation

Multifractal analysis (MFA) provides a framework for the global characterization of image textures by describing the spatial fluctuations of their local regularity based on the multifractal spectrum. Several works have shown the interest of using MFA for the description of homogeneous textures in images. Nevertheless, natural images can be composed of several textures and, in turn, multifractal properties associated with those textures. This paper introduces a Bayesian multifractal segmentation method to model and segment multifractal textures by jointly estimating the multifractal parameters and labels on images. For this, a computationally and statistically efficient multifractal parameter estimation model for wavelet leaders is firstly developed, defining different multifractality parameters to different regions of an image. Then, a multiscale Potts Markov random field is introduced as a prior to model the inherent spatial and scale correlations between the labels of the wavelet leaders. A Gibbs sampling methodology is employed to draw samples from the posterior distribution of the parameters. Numerical experiments are conducted on synthetic multifractal images to evaluate the performance of the proposed segmentation approach. The proposed method achieves superior performance compared to traditional unsupervised segmentation techniques as well as modern deep learning-based approaches, showing its effectiveness for multifractal image segmentation.

In-Flight Estimation of Instrument Spectral Response Functions Using Sparse Representations

Accurate estimates of Instrument Spectral Response Functions (ISRFs) are crucial in order to have a good characterization of high resolution spectrometers. Spectrometers are composed of different optical elements that can induce errors in the measurements and therefore need to be modeled as accurately as possible. Parametric models are currently used to estimate these response functions. However, these models cannot always take into account the diversity of ISRF shapes that are encountered in practical applications. This paper studies a new ISRF estimation method based on a sparse representation of atoms belonging to a dictionary. This method is applied to different high-resolution spectrometers in order to assess its reproducibility for multiple remote sensing missions. The proposed method is shown to be very competitive when compared to the more commonly used parametric models, and yields normalized ISRF estimation errors less than 1%.

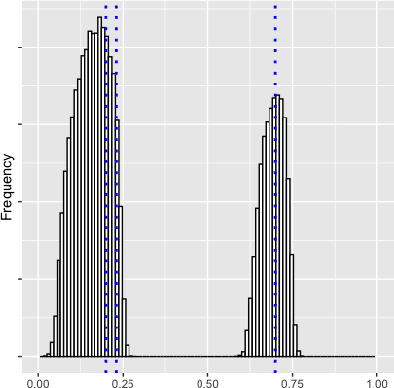
Multivariate selfsimilarity: Multiscale eigen-structures for selfsimilarity parameter estimation

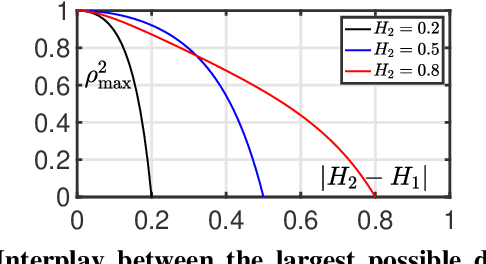
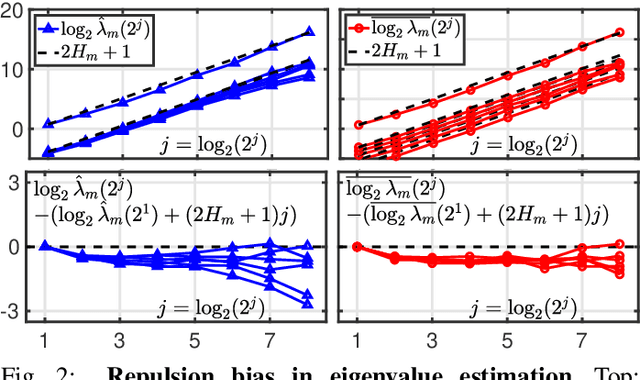
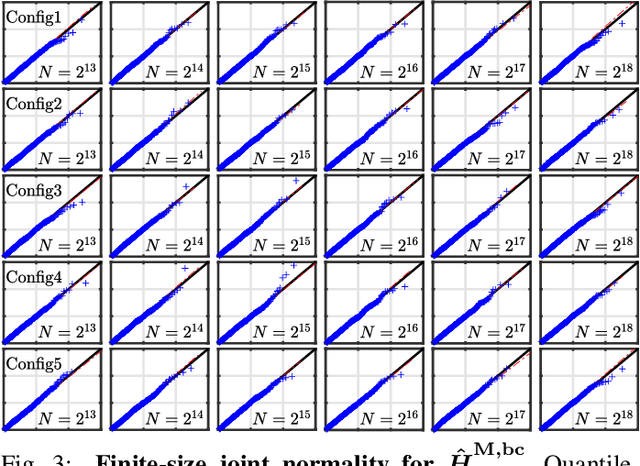
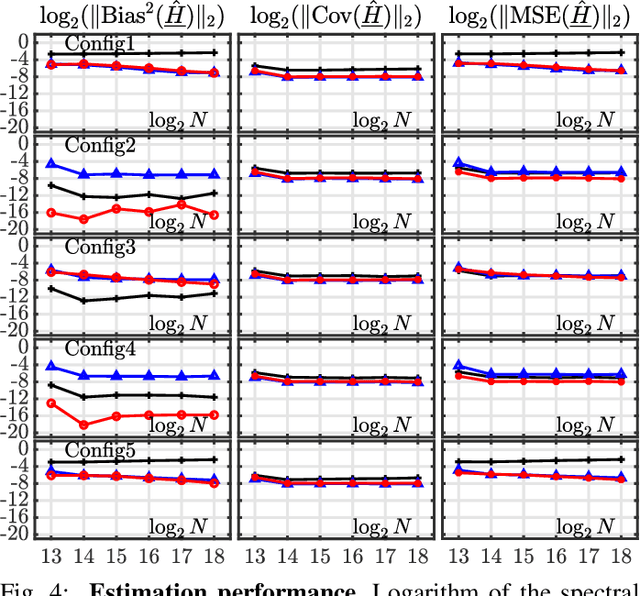
Scale-free dynamics, formalized by selfsimilarity, provides a versatile paradigm massively and ubiquitously used to model temporal dynamics in real-world data. However, its practical use has mostly remained univariate so far. By contrast, modern applications often demand multivariate data analysis. Accordingly, models for multivariate selfsimilarity were recently proposed. Nevertheless, they have remained rarely used in practice because of a lack of available robust estimation procedures for the vector of selfsimilarity parameters. Building upon recent mathematical developments, the present work puts forth an efficient estimation procedure based on the theoretical study of the multiscale eigenstructure of the wavelet spectrum of multivariate selfsimilar processes. The estimation performance is studied theoretically in the asymptotic limits of large scale and sample sizes, and computationally for finite-size samples. As a practical outcome, a fully operational and documented multivariate signal processing estimation toolbox is made freely available and is ready for practical use on real-world data. Its potential benefits are illustrated in epileptic seizure prediction from multi-channel EEG data.

Learning grounded word meaning representations on similarity graphs

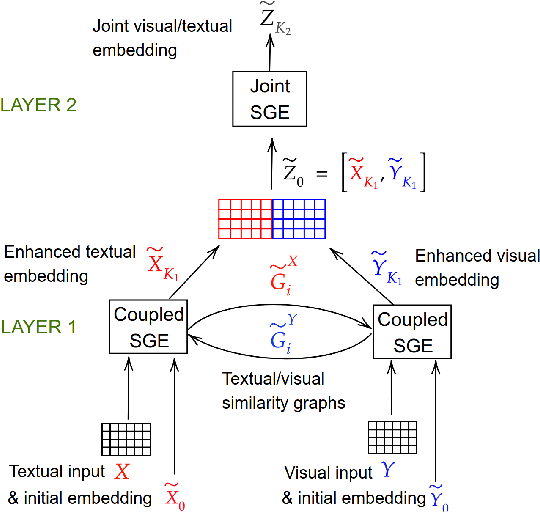
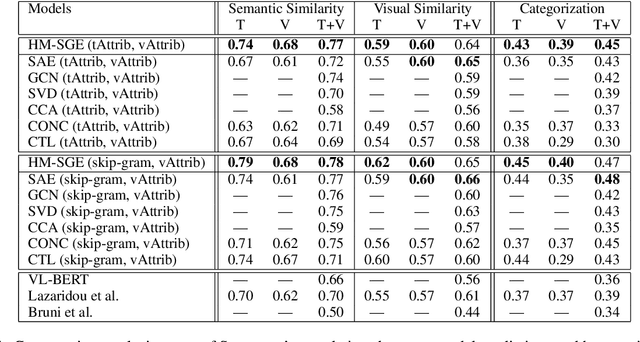
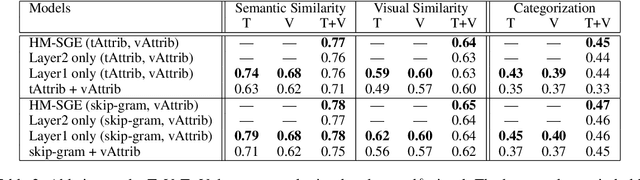
This paper introduces a novel approach to learn visually grounded meaning representations of words as low-dimensional node embeddings on an underlying graph hierarchy. The lower level of the hierarchy models modality-specific word representations through dedicated but communicating graphs, while the higher level puts these representations together on a single graph to learn a representation jointly from both modalities. The topology of each graph models similarity relations among words, and is estimated jointly with the graph embedding. The assumption underlying this model is that words sharing similar meaning correspond to communities in an underlying similarity graph in a low-dimensional space. We named this model Hierarchical Multi-Modal Similarity Graph Embedding (HM-SGE). Experimental results validate the ability of HM-SGE to simulate human similarity judgements and concept categorization, outperforming the state of the art.

Graph Constrained Data Representation Learning for Human Motion Segmentation

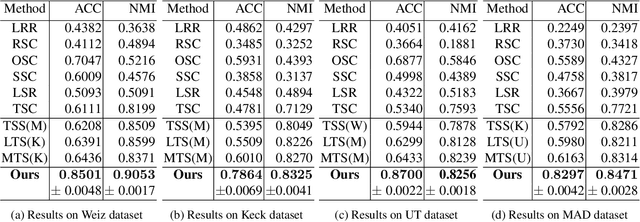
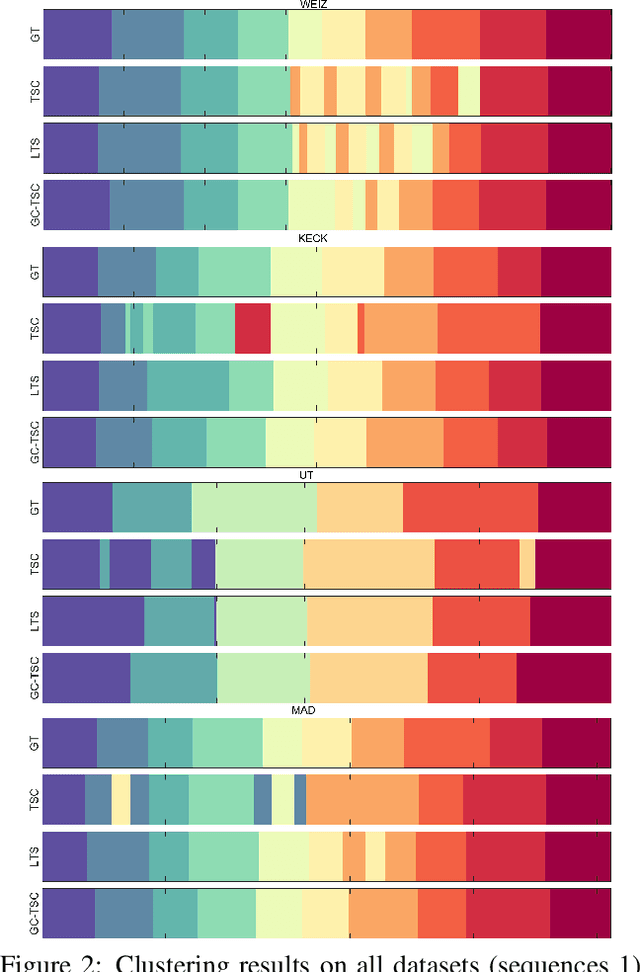
Recently, transfer subspace learning based approaches have shown to be a valid alternative to unsupervised subspace clustering and temporal data clustering for human motion segmentation (HMS). These approaches leverage prior knowledge from a source domain to improve clustering performance on a target domain, and currently they represent the state of the art in HMS. Bucking this trend, in this paper, we propose a novel unsupervised model that learns a representation of the data and digs clustering information from the data itself. Our model is reminiscent of temporal subspace clustering, but presents two critical differences. First, we learn an auxiliary data matrix that can deviate from the initial data, hence confer more degrees of freedom to the coding matrix. Second, we introduce a regularization term for this auxiliary data matrix that preserves the local geometrical structure present in the high-dimensional space. The proposed model is efficiently optimized by using an original Alternating Direction Method of Multipliers (ADMM) formulation allowing to learn jointly the auxiliary data representation, a nonnegative dictionary and a coding matrix. Experimental results on four benchmark datasets for HMS demonstrate that our approach achieves significantly better clustering performance then state-of-the-art methods, including both unsupervised and more recent semi-supervised transfer learning approaches.

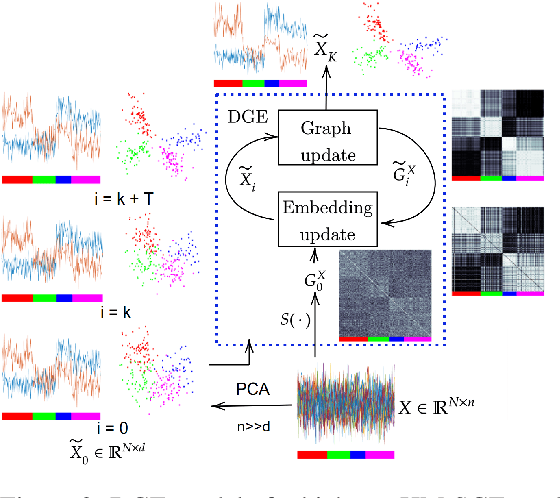
Learning event representations in image sequences by dynamic graph embedding

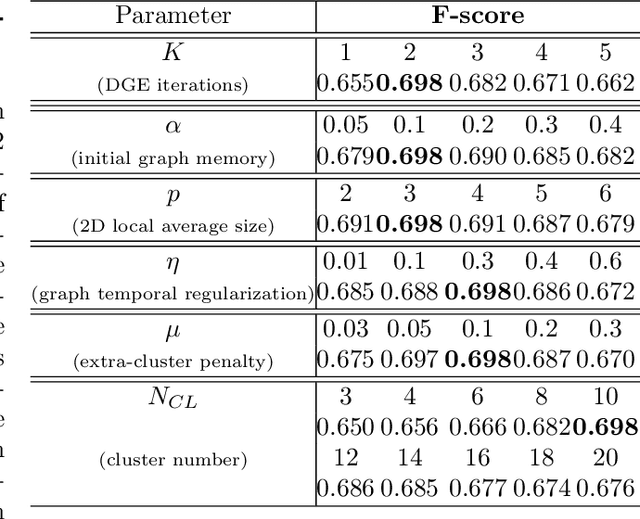
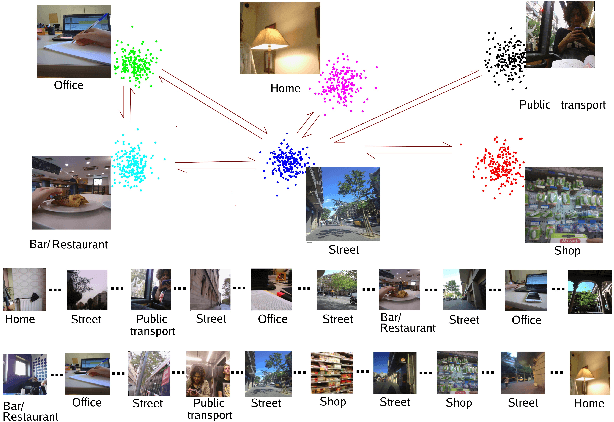
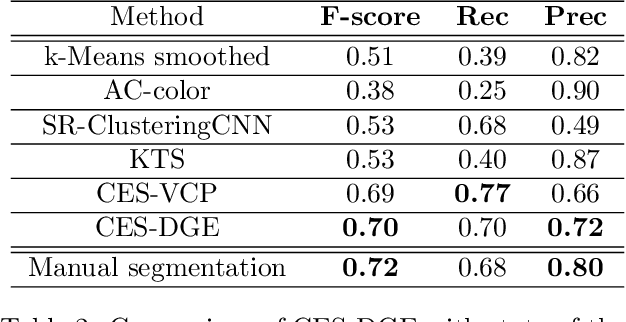
Recently, self-supervised learning has proved to be effective to learn representations of events in image sequences, where events are understood as sets of temporally adjacent images that are semantically perceived as a whole. However, although this approach does not require expensive manual annotations, it is data hungry and suffers from domain adaptation problems. As an alternative, in this work, we propose a novel approach for learning event representations named Dynamic Graph Embedding (DGE). The assumption underlying our model is that a sequence of images can be represented by a graph that encodes both semantic and temporal similarity. The key novelty of DGE is to learn jointly the graph and its graph embedding. At its core, DGE works by iterating over two steps: 1) updating the graph representing the semantic and temporal structure of the data based on the current data representation, and 2) updating the data representation to take into account the current data graph structure. The main advantage of DGE over state-of-the-art self-supervised approaches is that it does not require any training set, but instead learns iteratively from the data itself a low-dimensional embedding that reflects their temporal and semantic structure. Experimental results on two benchmark datasets of real image sequences captured at regular intervals demonstrate that the proposed DGE leads to effective event representations. In particular, it achieves robust temporal segmentation on the EDUBSeg and EDUBSeg-Desc benchmark datasets, outperforming the state of the art.

Enhancing temporal segmentation by nonlocal self-similarity

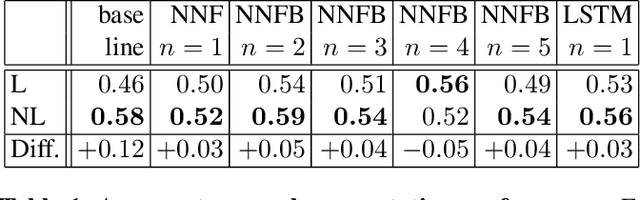
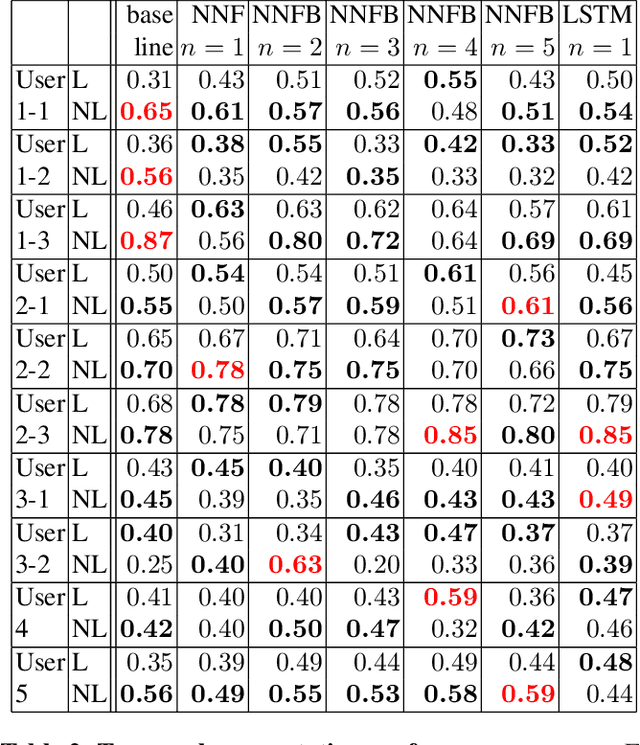
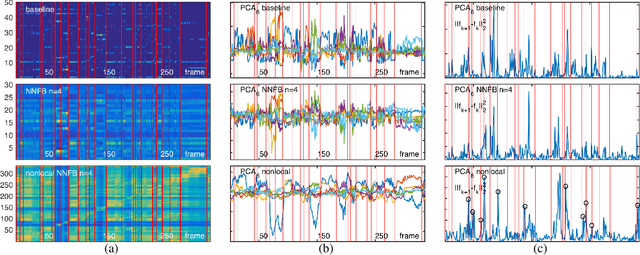
Temporal segmentation of untrimmed videos and photo-streams is currently an active area of research in computer vision and image processing. This paper proposes a new approach to improve the temporal segmentation of photo-streams. The method consists in enhancing image representations by encoding long-range temporal dependencies. Our key contribution is to take advantage of the temporal stationarity assumption of photostreams for modeling each frame by its nonlocal self-similarity function. The proposed approach is put to test on the EDUB-Seg dataset, a standard benchmark for egocentric photostream temporal segmentation. Starting from seven different (CNN based) image features, the method yields consistent improvements in event segmentation quality, leading to an average increase of F-measure of 3.71% with respect to the state of the art.

A Quasi-Newton algorithm on the orthogonal manifold for NMF with transform learning

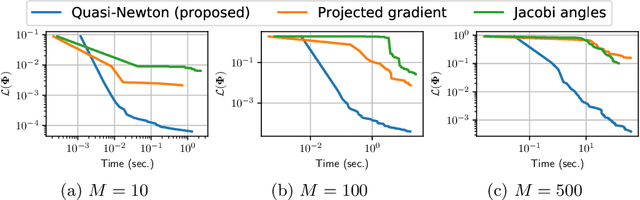
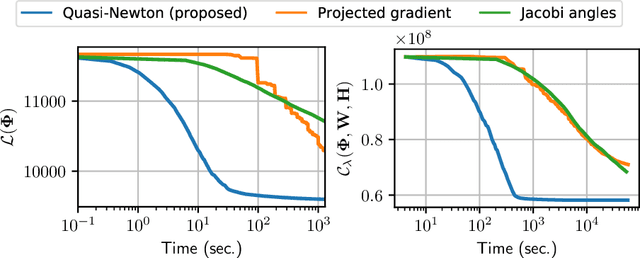
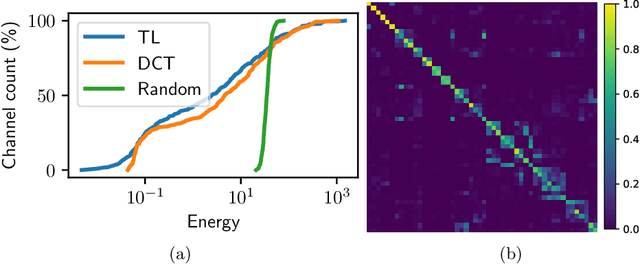
Nonnegative matrix factorization (NMF) is a popular method for audio spectral unmixing. While NMF is traditionally applied to off-the-shelf time-frequency representations based on the short-time Fourier or Cosine transforms, the ability to learn transforms from raw data attracts increasing attention. However, this adds an important computational overhead. When assumed orthogonal (like the Fourier or Cosine transforms), learning the transform yields a non-convex optimization problem on the orthogonal matrix manifold. In this paper, we derive a quasi-Newton method on the manifold using sparse approximations of the Hessian. Experiments on synthetic and real audio data show that the proposed algorithm out-performs state-of-the-art first-order and coordinate-descent methods by orders of magnitude. A Python package for fast TL-NMF is released online at https://github.com/pierreablin/tlnmf.

Nonnegative Matrix Factorization with Transform Learning

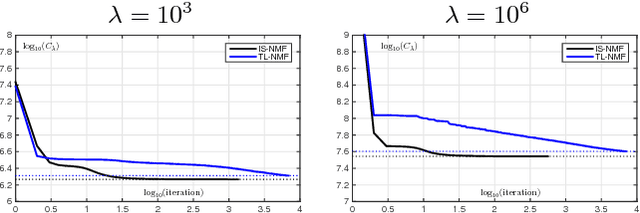
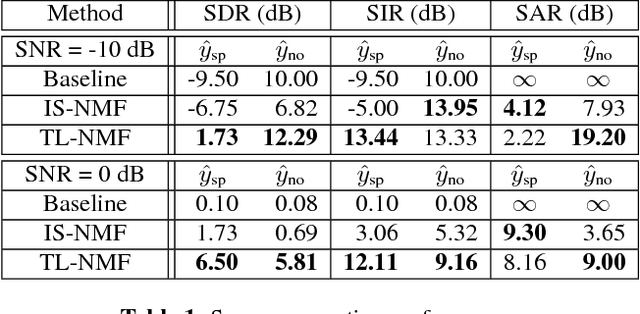
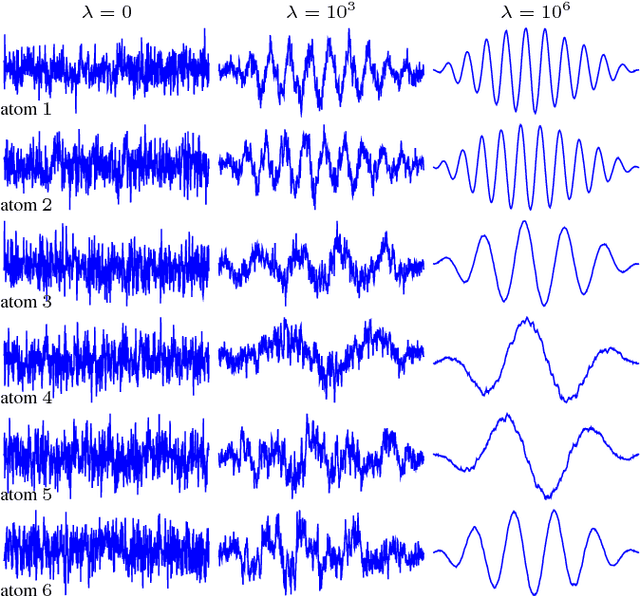
Traditional NMF-based signal decomposition relies on the factorization of spectral data, which is typically computed by means of short-time frequency transform. In this paper we propose to relax the choice of a pre-fixed transform and learn a short-time orthogonal transform together with the factorization. To this end, we formulate a regularized optimization problem reminiscent of conventional NMF, yet with the transform as additional unknown parameters, and design a novel block-descent algorithm enabling to find stationary points of this objective function. The proposed joint transform learning and factorization approach is tested for two audio signal processing experiments, illustrating its conceptual and practical benefits.