Multidimensional empirical wavelet transform

The empirical wavelet transform is a data-driven time-scale representation consisting of adaptive filters. Its robustness to data has made it the subject of intense developments and an increasing number of applications in the last decade. However, it has been mostly studied theoretically for signals so far and its extension to images is limited to a particular mother wavelet. This work presents a general framework for multidimensional empirical wavelet transform from any mother wavelet. In addition, it provides conditions to build wavelet frames for both continuous and discrete transforms.

Multivariate selfsimilarity: Multiscale eigen-structures for selfsimilarity parameter estimation

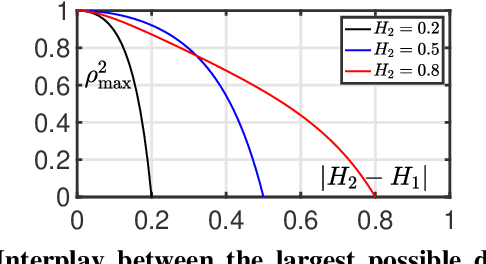
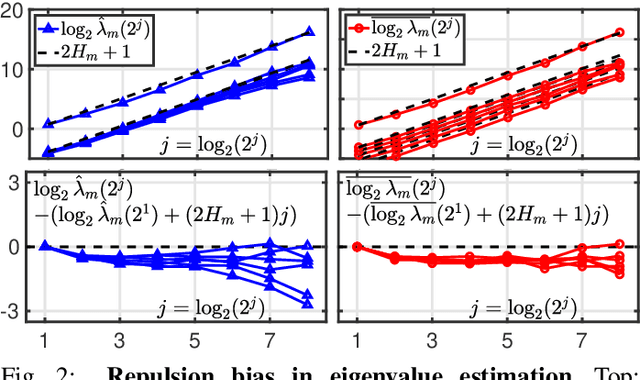
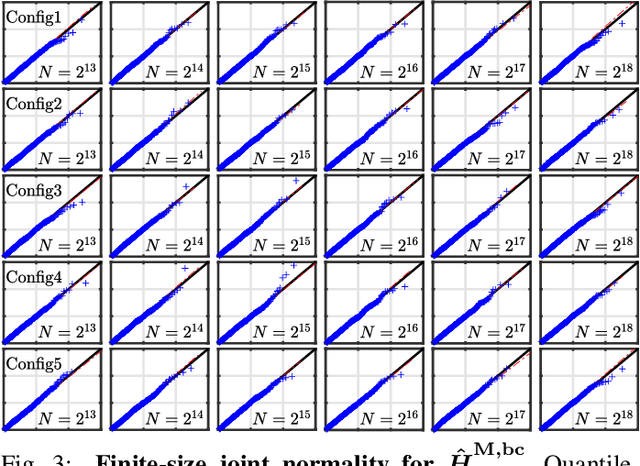
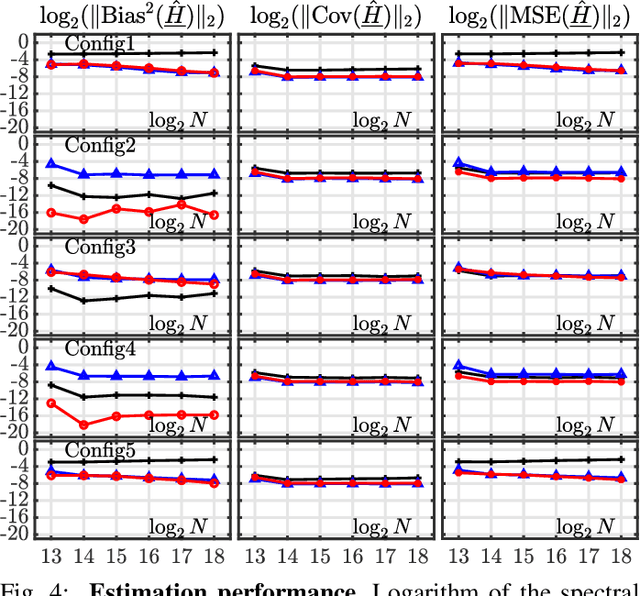
Scale-free dynamics, formalized by selfsimilarity, provides a versatile paradigm massively and ubiquitously used to model temporal dynamics in real-world data. However, its practical use has mostly remained univariate so far. By contrast, modern applications often demand multivariate data analysis. Accordingly, models for multivariate selfsimilarity were recently proposed. Nevertheless, they have remained rarely used in practice because of a lack of available robust estimation procedures for the vector of selfsimilarity parameters. Building upon recent mathematical developments, the present work puts forth an efficient estimation procedure based on the theoretical study of the multiscale eigenstructure of the wavelet spectrum of multivariate selfsimilar processes. The estimation performance is studied theoretically in the asymptotic limits of large scale and sample sizes, and computationally for finite-size samples. As a practical outcome, a fully operational and documented multivariate signal processing estimation toolbox is made freely available and is ready for practical use on real-world data. Its potential benefits are illustrated in epileptic seizure prediction from multi-channel EEG data.

Hyperparameter selection for the Discrete Mumford-Shah functional

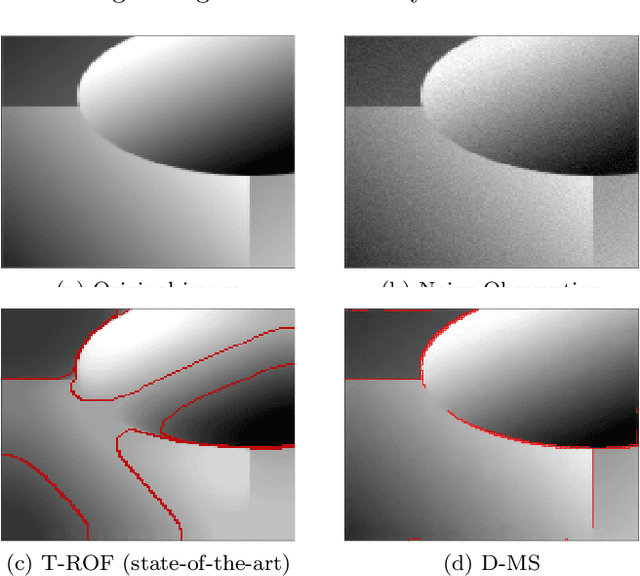
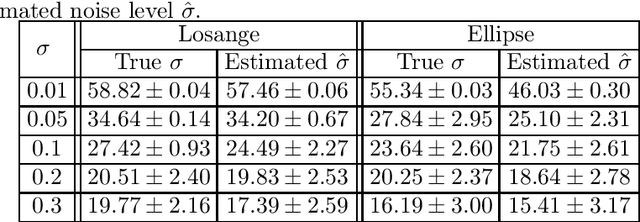
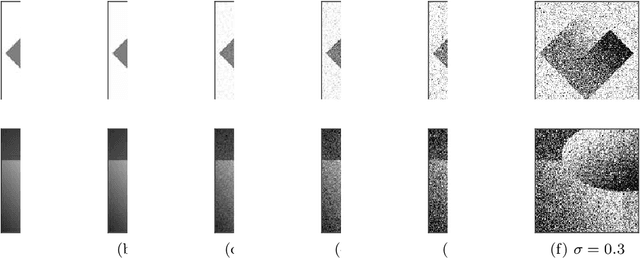
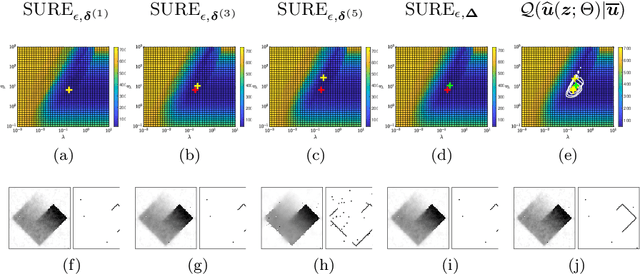
This work focuses on joint piecewise smooth image reconstruction and contour detection, formulated as the minimization of a discrete Mumford-Shah functional, performed via a theoretically grounded alternating minimization scheme. The bottleneck of such variational approaches lies in the need to finetune their hyperparameters, while not having access to ground truth data. To that aim, a Stein-like strategy providing optimal hyperparameters is designed, based on the minimization of an unbiased estimate of the quadratic risk. Efficient and automated minimization of the estimate of the risk crucially relies on an unbiased estimate of the gradient of the risk with respect to hyperparameters, whose practical implementation is performed thanks to a forward differentiation of the alternating scheme minimizing the Mumford-Shah functional, requiring exact differentiation of the proximity operators involved. Intensive numerical experiments are performed on synthetic images with different geometries and noise levels, assessing the accuracy and the robustness of the proposed procedure. The resulting parameterfree piecewise-smooth reconstruction and contour detection procedure, not requiring prior image processing expertise, is thus amenable to real-world applications.