Self-Supervised Learning for Image Super-Resolution and Deblurring

Self-supervised methods have recently proved to be nearly as effective as supervised methods in various imaging inverse problems, paving the way for learning-based methods in scientific and medical imaging applications where ground truth data is hard or expensive to obtain. This is the case in magnetic resonance imaging and computed tomography. These methods critically rely on invariance to translations and/or rotations of the image distribution to learn from incomplete measurement data alone. However, existing approaches fail to obtain competitive performances in the problems of image super-resolution and deblurring, which play a key role in most imaging systems. In this work, we show that invariance to translations and rotations is insufficient to learn from measurements that only contain low-frequency information. Instead, we propose a new self-supervised approach that leverages the fact that many image distributions are approximately scale-invariant, and that can be applied to any inverse problem where high-frequency information is lost in the measurement process. We demonstrate throughout a series of experiments on real datasets that the proposed method outperforms other self-supervised approaches, and obtains performances on par with fully supervised learning.

Multivariate selfsimilarity: Multiscale eigen-structures for selfsimilarity parameter estimation

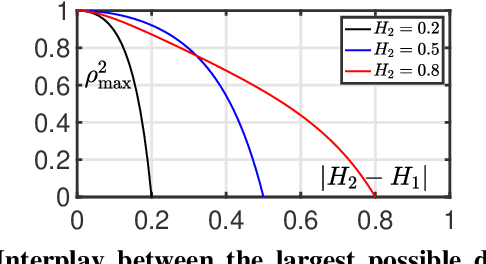
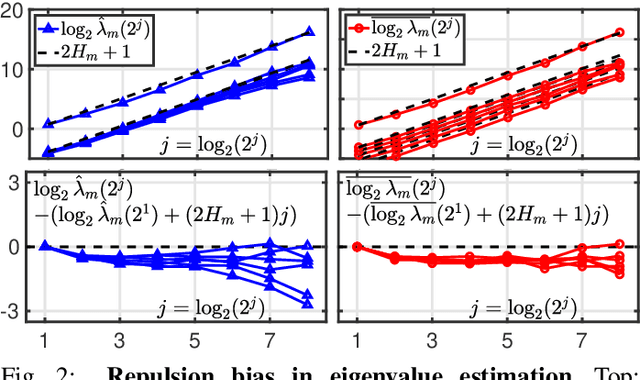
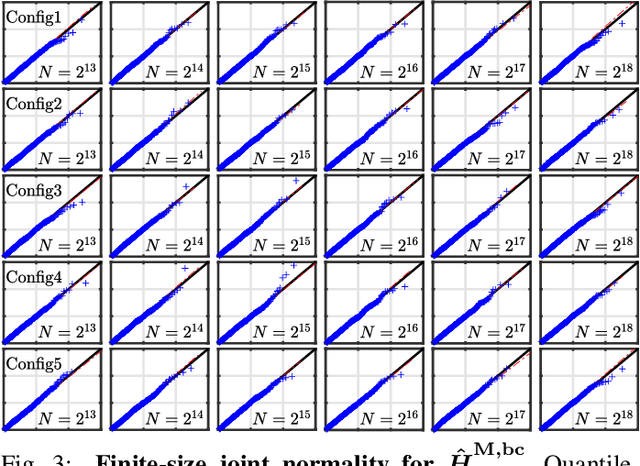
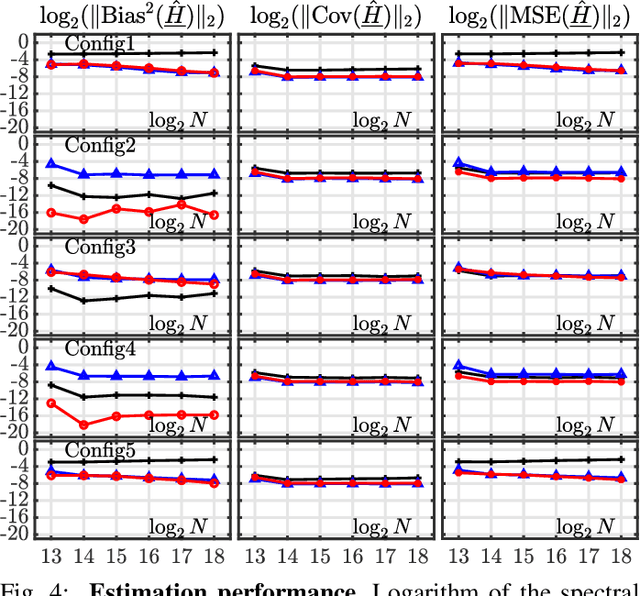
Scale-free dynamics, formalized by selfsimilarity, provides a versatile paradigm massively and ubiquitously used to model temporal dynamics in real-world data. However, its practical use has mostly remained univariate so far. By contrast, modern applications often demand multivariate data analysis. Accordingly, models for multivariate selfsimilarity were recently proposed. Nevertheless, they have remained rarely used in practice because of a lack of available robust estimation procedures for the vector of selfsimilarity parameters. Building upon recent mathematical developments, the present work puts forth an efficient estimation procedure based on the theoretical study of the multiscale eigenstructure of the wavelet spectrum of multivariate selfsimilar processes. The estimation performance is studied theoretically in the asymptotic limits of large scale and sample sizes, and computationally for finite-size samples. As a practical outcome, a fully operational and documented multivariate signal processing estimation toolbox is made freely available and is ready for practical use on real-world data. Its potential benefits are illustrated in epileptic seizure prediction from multi-channel EEG data.

Probabilistic forecasts of extreme heatwaves using convolutional neural networks in a regime of lack of data

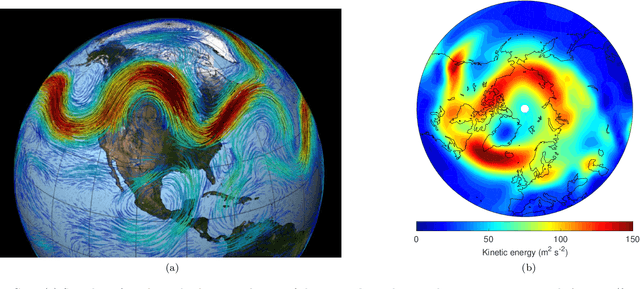
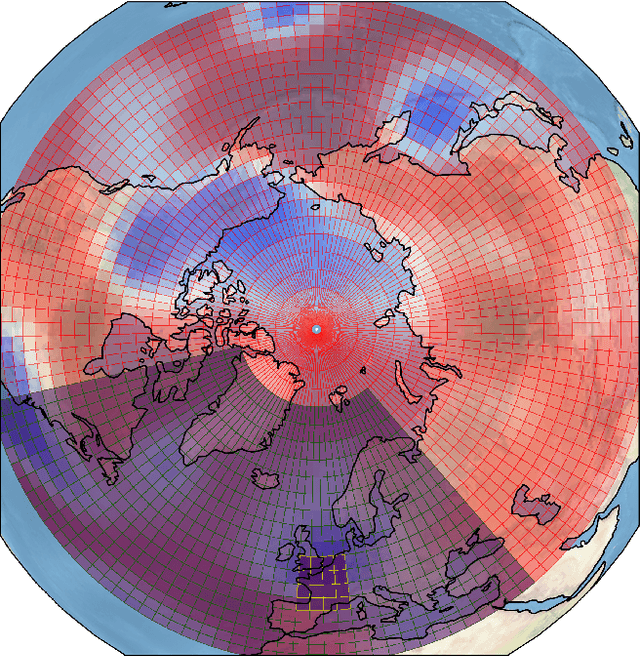
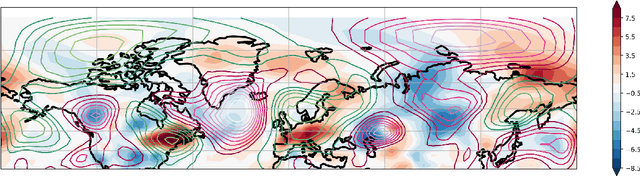
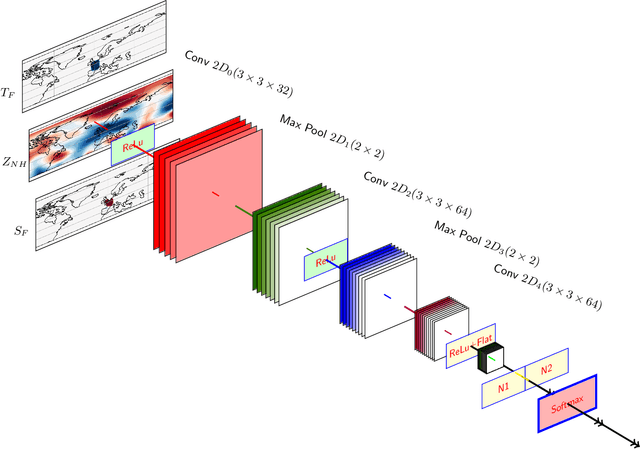
Understanding extreme events and their probability is key for the study of climate change impacts, risk assessment, adaptation, and the protection of living beings. In this work we develop a methodology to build forecasting models for extreme heatwaves. These models are based on convolutional neural networks, trained on extremely long 8,000-year climate model outputs. Because the relation between extreme events is intrinsically probabilistic, we emphasise probabilistic forecast and validation. We demonstrate that deep neural networks are suitable for this purpose for long lasting 14-day heatwaves over France, up to 15 days ahead of time for fast dynamical drivers (500 hPa geopotential height fields), and also at much longer lead times for slow physical drivers (soil moisture). The method is easily implemented and versatile. We find that the deep neural network selects extreme heatwaves associated with a North-Hemisphere wavenumber-3 pattern. We find that the 2 meter temperature field does not contain any new useful statistical information for heatwave forecast, when added to the 500 hPa geopotential height and soil moisture fields. The main scientific message is that training deep neural networks for predicting extreme heatwaves occurs in a regime of drastic lack of data. We suggest that this is likely the case for most other applications to large scale atmosphere and climate phenomena. We discuss perspectives for dealing with the lack of data regime, for instance rare event simulations, and how transfer learning may play a role in this latter task.

Covid19 Reproduction Number: Credibility Intervals by Blockwise Proximal Monte Carlo Samplers

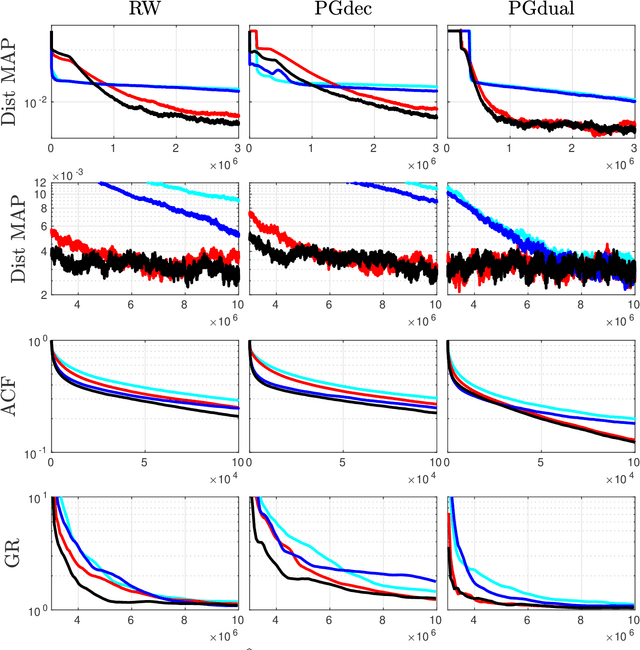
Monitoring the Covid19 pandemic constitutes a critical societal stake that received considerable research efforts. The intensity of the pandemic on a given territory is efficiently measured by the reproduction number, quantifying the rate of growth of daily new infections. Recently, estimates for the time evolution of the reproduction number were produced using an inverse problem formulation with a nonsmooth functional minimization. While it was designed to be robust to the limited quality of the Covid19 data (outliers, missing counts), the procedure lacks the ability to output credibility interval based estimates. This remains a severe limitation for practical use in actual pandemic monitoring by epidemiologists that the present work aims to overcome by use of Monte Carlo sampling. After interpretation of the functional into a Bayesian framework, several sampling schemes are tailored to adjust the nonsmooth nature of the resulting posterior distribution. The originality of the devised algorithms stems from combining a Langevin Monte Carlo sampling scheme with Proximal operators. Performance of the new algorithms in producing relevant credibility intervals for the reproduction number estimates and denoised counts are compared. Assessment is conducted on real daily new infection counts made available by the Johns Hopkins University. The interest of the devised monitoring tools are illustrated on Covid19 data from several different countries.

Hyperparameter selection for the Discrete Mumford-Shah functional

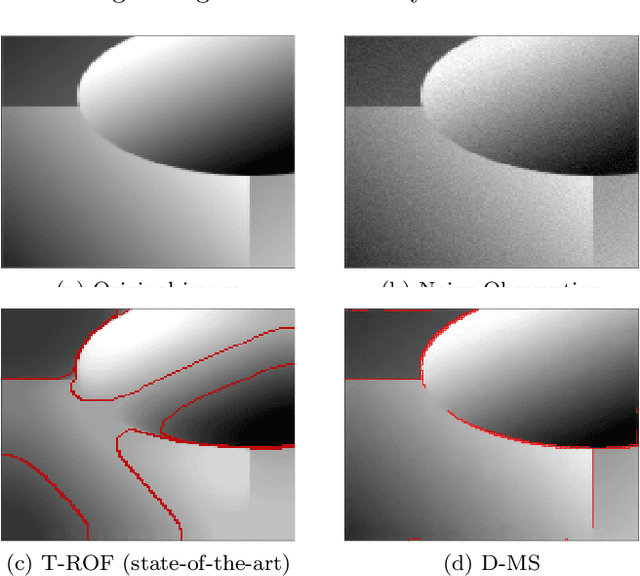
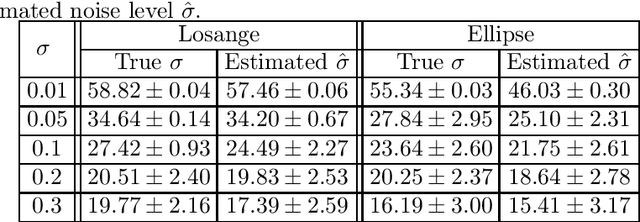
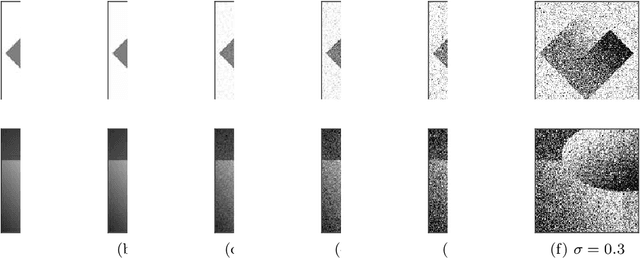
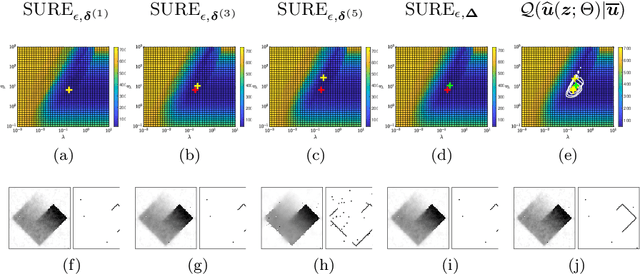
This work focuses on joint piecewise smooth image reconstruction and contour detection, formulated as the minimization of a discrete Mumford-Shah functional, performed via a theoretically grounded alternating minimization scheme. The bottleneck of such variational approaches lies in the need to finetune their hyperparameters, while not having access to ground truth data. To that aim, a Stein-like strategy providing optimal hyperparameters is designed, based on the minimization of an unbiased estimate of the quadratic risk. Efficient and automated minimization of the estimate of the risk crucially relies on an unbiased estimate of the gradient of the risk with respect to hyperparameters, whose practical implementation is performed thanks to a forward differentiation of the alternating scheme minimizing the Mumford-Shah functional, requiring exact differentiation of the proximity operators involved. Intensive numerical experiments are performed on synthetic images with different geometries and noise levels, assessing the accuracy and the robustness of the proposed procedure. The resulting parameterfree piecewise-smooth reconstruction and contour detection procedure, not requiring prior image processing expertise, is thus amenable to real-world applications.

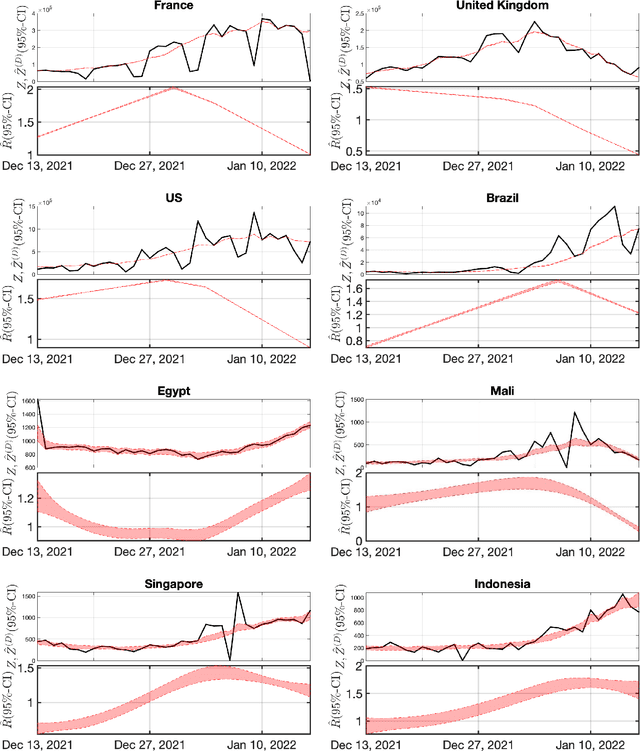
Nonsmooth convex optimization to estimate the Covid-19 reproduction number space-time evolution with robustness against low quality data

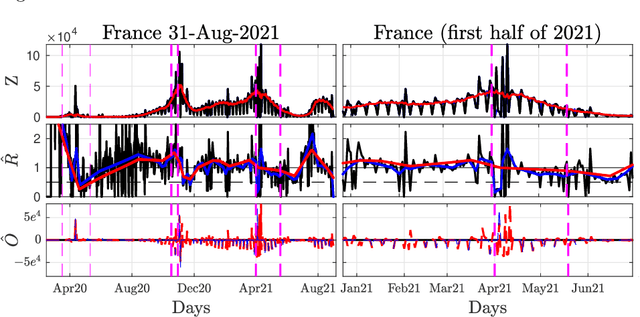
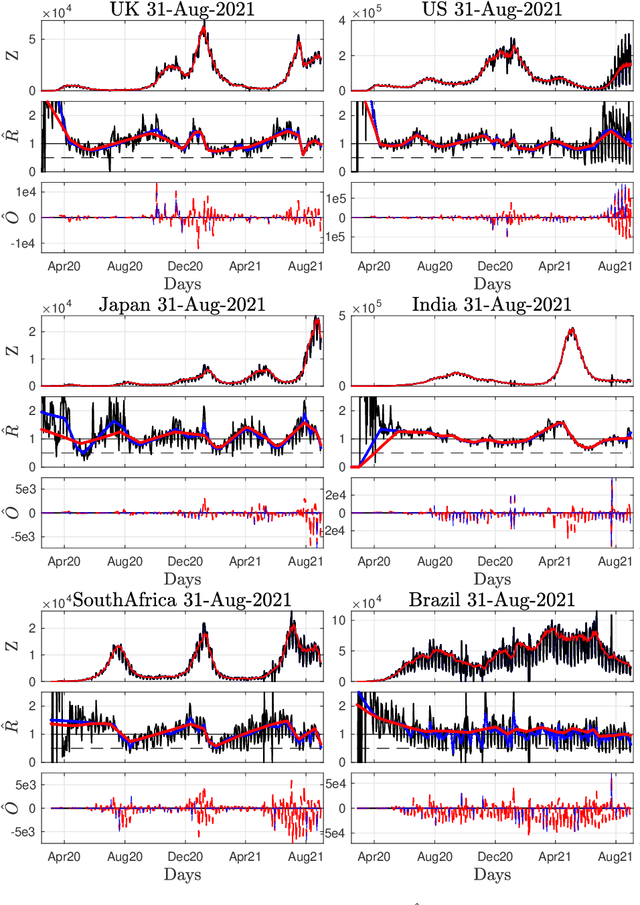
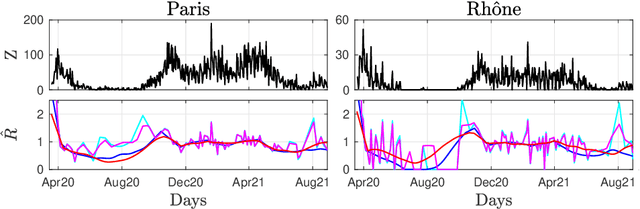
Daily pandemic surveillance, often achieved through the estimation of the reproduction number, constitutes a critical challenge for national health authorities to design countermeasures. In an earlier work, we proposed to formulate the estimation of the reproduction number as an optimization problem, combining data-model fidelity and space-time regularity constraints, solved by nonsmooth convex proximal minimizations. Though promising, that first formulation significantly lacks robustness against the Covid-19 data low quality (irrelevant or missing counts, pseudo-seasonalities,.. .) stemming from the emergency and crisis context, which significantly impairs accurate pandemic evolution assessments. The present work aims to overcome these limitations by carefully crafting a functional permitting to estimate jointly, in a single step, the reproduction number and outliers defined to model low quality data. This functional also enforces epidemiology-driven regularity properties for the reproduction number estimates, while preserving convexity, thus permitting the design of efficient minimization algorithms, based on proximity operators that are derived analytically. The explicit convergence of the proposed algorithm is proven theoretically. Its relevance is quantified on real Covid-19 data, consisting of daily new infection counts for 200+ countries and for the 96 metropolitan France counties, publicly available at Johns Hopkins University and Sant{\'e}-Publique-France. The procedure permits automated daily updates of these estimates, reported via animated and interactive maps. Open-source estimation procedures will be made publicly available.

Deep Learning based Extreme Heatwave Forecast

Forecasting the occurrence of heatwaves constitutes a challenging issue, yet of major societal stake, because extreme events are not often observed and (very) costly to simulate from physics-driven numerical models. The present work aims to explore the use of Deep Learning architectures as alternative strategies to predict extreme heatwaves occurrences from a very limited amount of available relevant climate data. This implies addressing issues such as the aggregation of climate data of different natures, the class-size imbalance that is intrinsically associated with rare event prediction, and the potential benefits of transfer learning to address the nested nature of extreme events (naturally included in less extreme ones). Using 1000 years of state-of-the-art PlaSim Planete Simulator Climate Model data, it is shown that Convolutional Neural Network-based Deep Learning frameworks, with large-class undersampling and transfer learning achieve significant performance in forecasting the occurrence of extreme heatwaves, at three different levels of intensity, and as early as 15 days in advance from the restricted observation, for a single time (single snapshoot) of only two spatial fields of climate data, surface temperature and geopotential height.

Multiview Variational Graph Autoencoders for Canonical Correlation Analysis

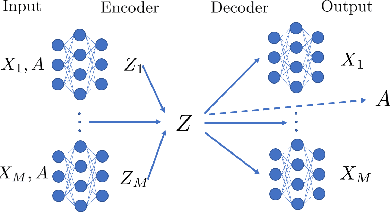
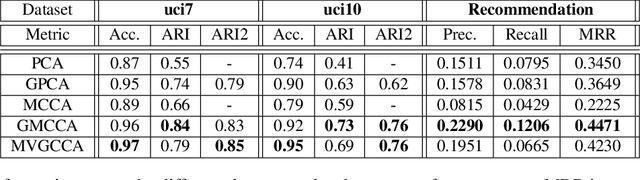
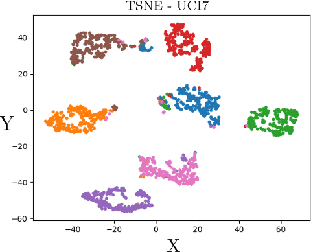
We present a novel multiview canonical correlation analysis model based on a variational approach. This is the first nonlinear model that takes into account the available graph-based geometric constraints while being scalable for processing large scale datasets with multiple views. It is based on an autoencoder architecture with graph convolutional neural network layers. We experiment with our approach on classification, clustering, and recommendation tasks on real datasets. The algorithm is competitive with state-of-the-art multiview representation learning techniques.

Automated data-driven selection of the hyperparameters for Total-Variation based texture segmentation

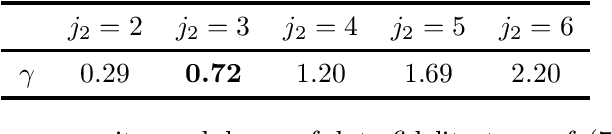
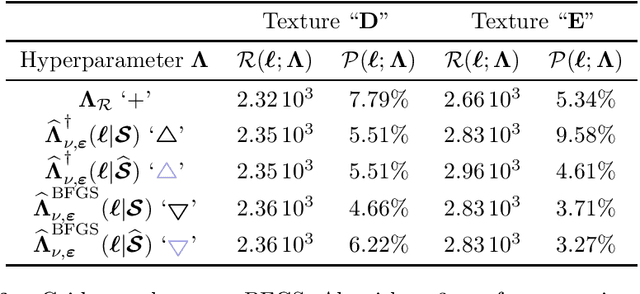
Penalized Least Squares are widely used in signal and image processing. Yet, it suffers from a major limitation since it requires fine-tuning of the regularization parameters. Under assumptions on the noise probability distribution, Stein-based approaches provide unbiased estimator of the quadratic risk. The Generalized Stein Unbiased Risk Estimator is revisited to handle correlated Gaussian noise without requiring to invert the covariance matrix. Then, in order to avoid expansive grid search, it is necessary to design algorithmic scheme minimizing the quadratic risk with respect to regularization parameters. This work extends the Stein's Unbiased GrAdient estimator of the Risk of Deledalle et al. to the case of correlated Gaussian noise, deriving a general automatic tuning of regularization parameters. First, the theoretical asymptotic unbiasedness of the gradient estimator is demonstrated in the case of general correlated Gaussian noise. Then, the proposed parameter selection strategy is particularized to fractal texture segmentation, where problem formulation naturally entails inter-scale and spatially correlated noise. Numerical assessment is provided, as well as discussion of the practical issues.

$L^γ$-PageRank for Semi-Supervised Learning

PageRank for Semi-Supervised Learning has shown to leverage data structures and limited tagged examples to yield meaningful classification. Despite successes, classification performance can still be improved, particularly in cases of fuzzy graphs or unbalanced labeled data. To address such limitations, a novel approach based on powers of the Laplacian matrix $L^\gamma$ ($\gamma > 0$), referred to as $L^\gamma$-PageRank, is proposed. Its theoretical study shows that it operates on signed graphs, where nodes belonging to one same class are more likely to share positive edges while nodes from different classes are more likely to be connected with negative edges. It is shown that by selecting an optimal $\gamma$, classification performance can be significantly enhanced. A procedure for the automated estimation of the optimal $\gamma$, from a unique observation of data, is devised and assessed. Experiments on several datasets demonstrate the effectiveness of both $L^\gamma$-PageRank classification and the optimal $\gamma$ estimation.