The Analytic Stockwell Transform and its Zeros

A recent original line of research in time--frequency analysis has shifted the interest in energy maxima toward zeros. Initially motivated by the intriguing uniform spread of the zeros of the spectrogram of white noise, it has led to fruitful theoretical developments combining probability theory, complex analysis and signal processing. In this vein, the present work proposes a characterization of the zeros of the Stockwell Transform of white noise, which consists in an hybrid time--frequency multiresolution representation. First of all, an analytic version of the Stockwell Transform is designed. Then, analyticity is leveraged to establish a connection with the hyperbolic Gaussian Analytic Function, whose zero set is invariant under the isometries of the Poincar\'e disk. Finally, the theoretical spatial statistics of the zeros of the hyperbolic Gaussian Analytic Function and the empirical statistics of the zeros the Analytic Stockwell Transform of white noise are compared through intensive Monte Carlo simulations, supporting the established connection. A publicly available documented Python toolbox accompanies this work.

Point Processes and spatial statistics in time-frequency analysis

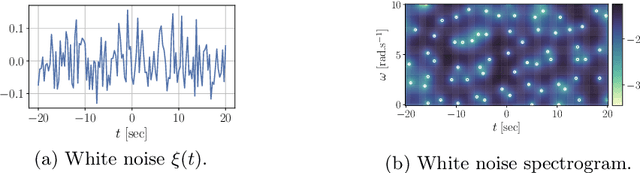
A finite-energy signal is represented by a square-integrable, complex-valued function $t\mapsto s(t)$ of a real variable $t$, interpreted as time. Similarly, a noisy signal is represented by a random process. Time-frequency analysis, a subfield of signal processing, amounts to describing the temporal evolution of the frequency content of a signal. Loosely speaking, if $s$ is the audio recording of a musical piece, time-frequency analysis somehow consists in writing the musical score of the piece. Mathematically, the operation is performed through a transform $\mathcal{V}$, mapping $s \in L^2(\mathbb{R})$ onto a complex-valued function $\mathcal{V}s \in L^2(\mathbb{R}^2)$ of time $t$ and angular frequency $\omega$. The squared modulus $(t, \omega) \mapsto \vert\mathcal{V}s(t,\omega)\vert^2$ of the time-frequency representation is known as the spectrogram of $s$; in the musical score analogy, a peaked spectrogram at $(t_0,\omega_0)$ corresponds to a musical note at angular frequency $\omega_0$ localized at time $t_0$. More generally, the intuition is that upper level sets of the spectrogram contain relevant information about in the original signal. Hence, many signal processing algorithms revolve around identifying maxima of the spectrogram. In contrast, zeros of the spectrogram indicate perfect silence, that is, a time at which a particular frequency is absent. Assimilating $\mathbb{R}^2$ to $\mathbb{C}$ through $z = \omega + \mathrm{i}t$, this chapter focuses on time-frequency transforms $\mathcal{V}$ that map signals to analytic functions. The zeros of the spectrogram of a noisy signal are then the zeros of a random analytic function, hence forming a Point Process in $\mathbb{C}$. This chapter is devoted to the study of these Point Processes, to their links with zeros of Gaussian Analytic Functions, and to designing signal detection and denoising algorithms using spatial statistics.

Covid19 Reproduction Number: Credibility Intervals by Blockwise Proximal Monte Carlo Samplers

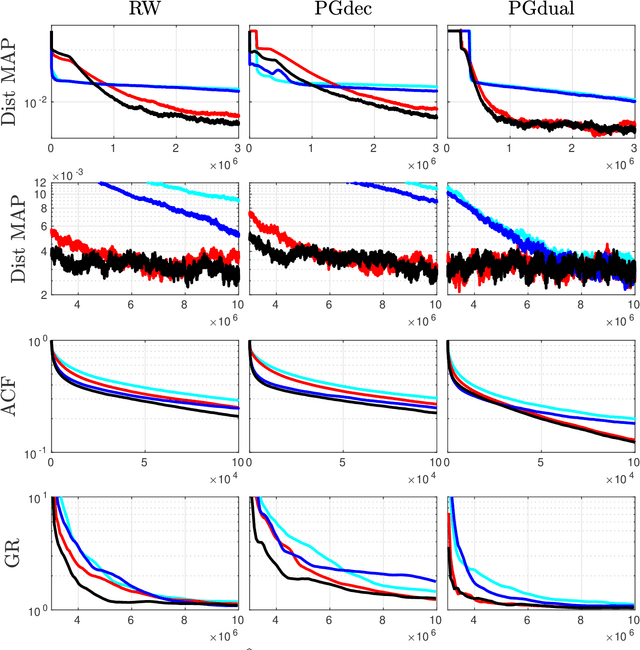
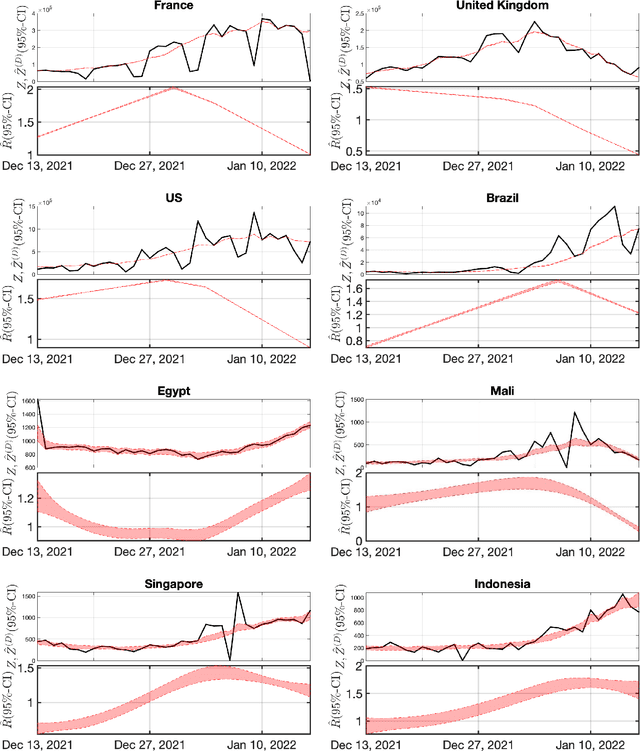
Monitoring the Covid19 pandemic constitutes a critical societal stake that received considerable research efforts. The intensity of the pandemic on a given territory is efficiently measured by the reproduction number, quantifying the rate of growth of daily new infections. Recently, estimates for the time evolution of the reproduction number were produced using an inverse problem formulation with a nonsmooth functional minimization. While it was designed to be robust to the limited quality of the Covid19 data (outliers, missing counts), the procedure lacks the ability to output credibility interval based estimates. This remains a severe limitation for practical use in actual pandemic monitoring by epidemiologists that the present work aims to overcome by use of Monte Carlo sampling. After interpretation of the functional into a Bayesian framework, several sampling schemes are tailored to adjust the nonsmooth nature of the resulting posterior distribution. The originality of the devised algorithms stems from combining a Langevin Monte Carlo sampling scheme with Proximal operators. Performance of the new algorithms in producing relevant credibility intervals for the reproduction number estimates and denoised counts are compared. Assessment is conducted on real daily new infection counts made available by the Johns Hopkins University. The interest of the devised monitoring tools are illustrated on Covid19 data from several different countries.

A covariant, discrete time-frequency representation tailored for zero-based signal detection

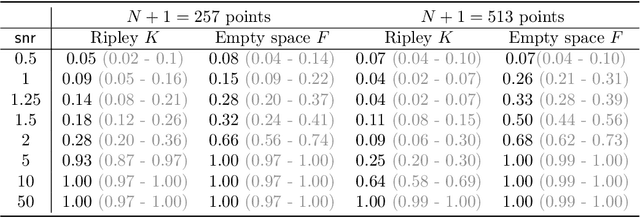
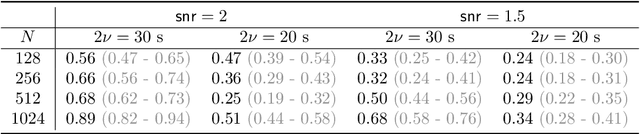
Recent work in time-frequency analysis proposed to switch the focus from the maxima of the spectrogram toward its zeros. The zeros of signals in white Gaussian noise indeed form a random point pattern with a very stable structure. Using modern spatial statistics tools on the pattern of zeros of a spectrogram has led to component disentanglement and signal detection procedures. The major bottlenecks of this approach are the discretization of the Short-Time Fourier Transform and the necessarily bounded observation window in the time-frequency plane. Both impact the estimation of summary statistics of the zeros, which are then used in standard statistical tests. To circumvent these limitations, we propose a generalized time-frequency representation, which we call the Kravchuk transform. It naturally applies to finite signals, i.e., finite-dimensional vectors. The corresponding phase space, instead of the whole time-frequency plane, is compact, and particularly amenable to spatial statistics. On top of this, the Kravchuk transform has several natural properties for signal processing, among which covariance under the action of SO(3), invertibility and symmetry with respect to complex conjugation. We further show that the point process of the zeros of the Kravchuk transform of discrete white Gaussian noise coincides in law with the zeros of the spherical Gaussian Analytic Function. This implies that the law of the zeros is invariant under isometries of the sphere. Elaborating on this theorem, we develop a procedure for signal detection based on the spatial statistics of the zeros of the Kravchuk spectrogram. The statistical power of this procedure is assessed by intensive numerical simulation, and compares favorably with respect to state-of-the-art zeros-based detection procedures. Furthermore it appears to be particularly robust to both low signal-to-noise ratio and small number of samples.

Hyperparameter selection for the Discrete Mumford-Shah functional

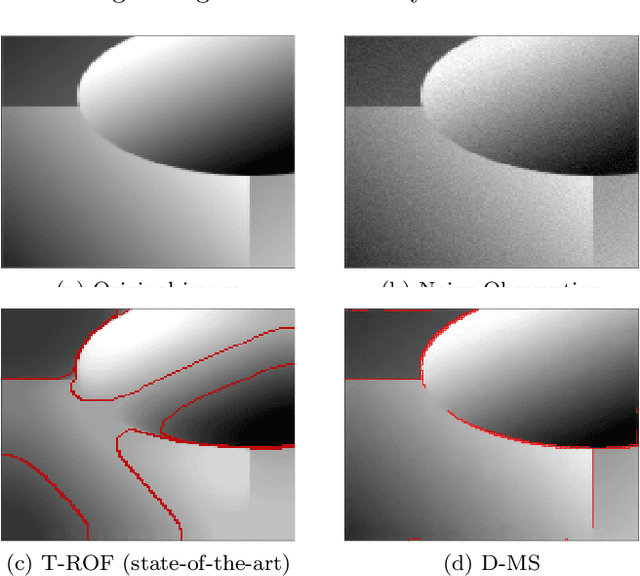
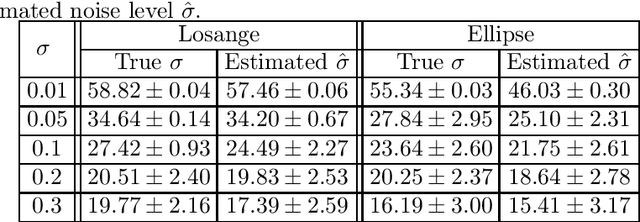
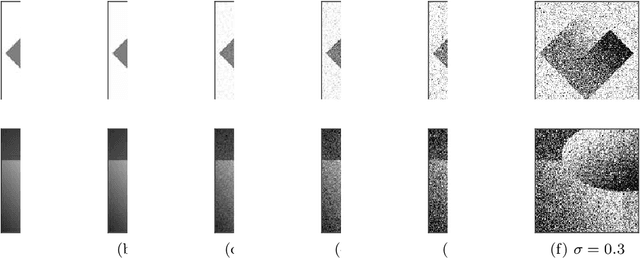
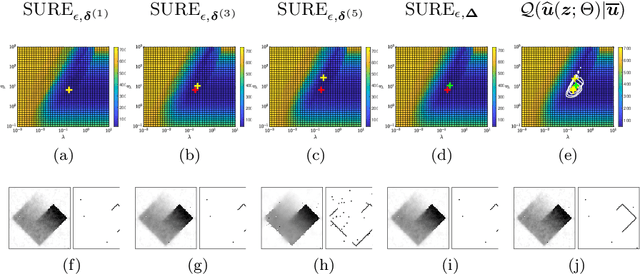
This work focuses on joint piecewise smooth image reconstruction and contour detection, formulated as the minimization of a discrete Mumford-Shah functional, performed via a theoretically grounded alternating minimization scheme. The bottleneck of such variational approaches lies in the need to finetune their hyperparameters, while not having access to ground truth data. To that aim, a Stein-like strategy providing optimal hyperparameters is designed, based on the minimization of an unbiased estimate of the quadratic risk. Efficient and automated minimization of the estimate of the risk crucially relies on an unbiased estimate of the gradient of the risk with respect to hyperparameters, whose practical implementation is performed thanks to a forward differentiation of the alternating scheme minimizing the Mumford-Shah functional, requiring exact differentiation of the proximity operators involved. Intensive numerical experiments are performed on synthetic images with different geometries and noise levels, assessing the accuracy and the robustness of the proposed procedure. The resulting parameterfree piecewise-smooth reconstruction and contour detection procedure, not requiring prior image processing expertise, is thus amenable to real-world applications.

Nonsmooth convex optimization to estimate the Covid-19 reproduction number space-time evolution with robustness against low quality data

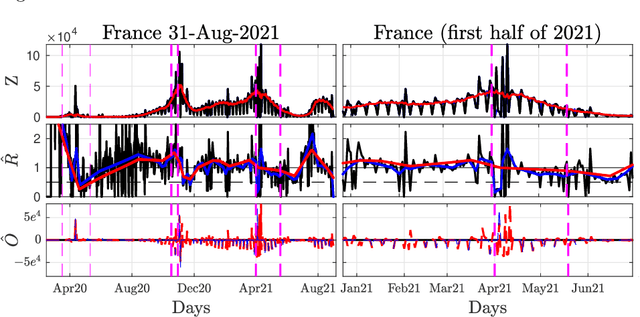
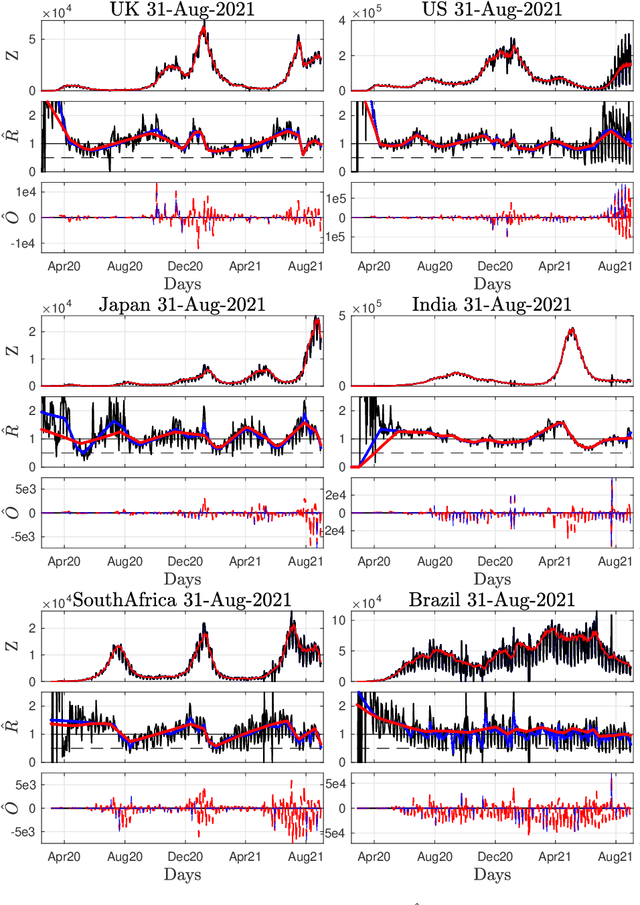
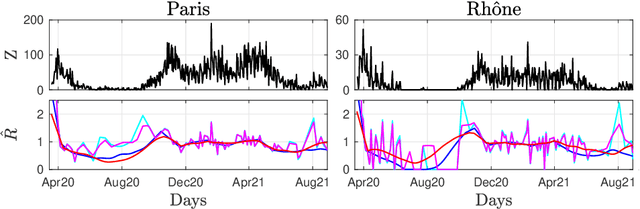
Daily pandemic surveillance, often achieved through the estimation of the reproduction number, constitutes a critical challenge for national health authorities to design countermeasures. In an earlier work, we proposed to formulate the estimation of the reproduction number as an optimization problem, combining data-model fidelity and space-time regularity constraints, solved by nonsmooth convex proximal minimizations. Though promising, that first formulation significantly lacks robustness against the Covid-19 data low quality (irrelevant or missing counts, pseudo-seasonalities,.. .) stemming from the emergency and crisis context, which significantly impairs accurate pandemic evolution assessments. The present work aims to overcome these limitations by carefully crafting a functional permitting to estimate jointly, in a single step, the reproduction number and outliers defined to model low quality data. This functional also enforces epidemiology-driven regularity properties for the reproduction number estimates, while preserving convexity, thus permitting the design of efficient minimization algorithms, based on proximity operators that are derived analytically. The explicit convergence of the proposed algorithm is proven theoretically. Its relevance is quantified on real Covid-19 data, consisting of daily new infection counts for 200+ countries and for the 96 metropolitan France counties, publicly available at Johns Hopkins University and Sant{\'e}-Publique-France. The procedure permits automated daily updates of these estimates, reported via animated and interactive maps. Open-source estimation procedures will be made publicly available.

Automated data-driven selection of the hyperparameters for Total-Variation based texture segmentation

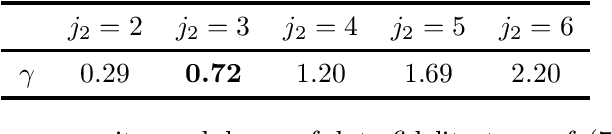
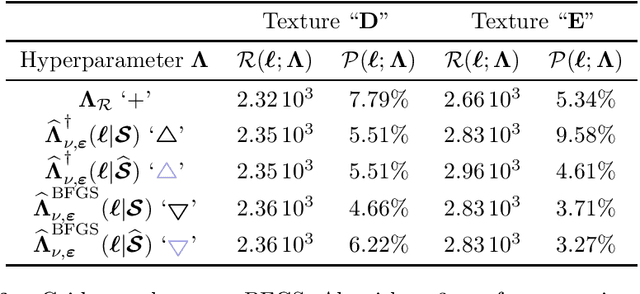
Penalized Least Squares are widely used in signal and image processing. Yet, it suffers from a major limitation since it requires fine-tuning of the regularization parameters. Under assumptions on the noise probability distribution, Stein-based approaches provide unbiased estimator of the quadratic risk. The Generalized Stein Unbiased Risk Estimator is revisited to handle correlated Gaussian noise without requiring to invert the covariance matrix. Then, in order to avoid expansive grid search, it is necessary to design algorithmic scheme minimizing the quadratic risk with respect to regularization parameters. This work extends the Stein's Unbiased GrAdient estimator of the Risk of Deledalle et al. to the case of correlated Gaussian noise, deriving a general automatic tuning of regularization parameters. First, the theoretical asymptotic unbiasedness of the gradient estimator is demonstrated in the case of general correlated Gaussian noise. Then, the proposed parameter selection strategy is particularized to fractal texture segmentation, where problem formulation naturally entails inter-scale and spatially correlated noise. Numerical assessment is provided, as well as discussion of the practical issues.