Stochastic Approximation Beyond Gradient for Signal Processing and Machine Learning

Stochastic approximation (SA) is a classical algorithm that has had since the early days a huge impact on signal processing, and nowadays on machine learning, due to the necessity to deal with a large amount of data observed with uncertainties. An exemplar special case of SA pertains to the popular stochastic (sub)gradient algorithm which is the working horse behind many important applications. A lesser-known fact is that the SA scheme also extends to non-stochastic-gradient algorithms such as compressed stochastic gradient, stochastic expectation-maximization, and a number of reinforcement learning algorithms. The aim of this article is to overview and introduce the non-stochastic-gradient perspectives of SA to the signal processing and machine learning audiences through presenting a design guideline of SA algorithms backed by theories. Our central theme is to propose a general framework that unifies existing theories of SA, including its non-asymptotic and asymptotic convergence results, and demonstrate their applications on popular non-stochastic-gradient algorithms. We build our analysis framework based on classes of Lyapunov functions that satisfy a variety of mild conditions. We draw connections between non-stochastic-gradient algorithms and scenarios when the Lyapunov function is smooth, convex, or strongly convex. Using the said framework, we illustrate the convergence properties of the non-stochastic-gradient algorithms using concrete examples. Extensions to the emerging variance reduction techniques for improved sample complexity will also be discussed.

Stochastic Variable Metric Proximal Gradient with variance reduction for non-convex composite optimization

This paper introduces a novel algorithm, the Perturbed Proximal Preconditioned SPIDER algorithm (3P-SPIDER), designed to solve finite sum non-convex composite optimization. It is a stochastic Variable Metric Forward-Backward algorithm, which allows approximate preconditioned forward operator and uses a variable metric proximity operator as the backward operator; it also proposes a mini-batch strategy with variance reduction to address the finite sum setting. We show that 3P-SPIDER extends some Stochastic preconditioned Gradient Descent-based algorithms and some Incremental Expectation Maximization algorithms to composite optimization and to the case the forward operator can not be computed in closed form. We also provide an explicit control of convergence in expectation of 3P-SPIDER, and study its complexity in order to satisfy the epsilon-approximate stationary condition. Our results are the first to combine the composite non-convex optimization setting, a variance reduction technique to tackle the finite sum setting by using a minibatch strategy and, to allow deterministic or random approximations of the preconditioned forward operator. Finally, through an application to inference in a logistic regression model with random effects, we numerically compare 3P-SPIDER to other stochastic forward-backward algorithms and discuss the role of some design parameters of 3P-SPIDER.

Covid19 Reproduction Number: Credibility Intervals by Blockwise Proximal Monte Carlo Samplers

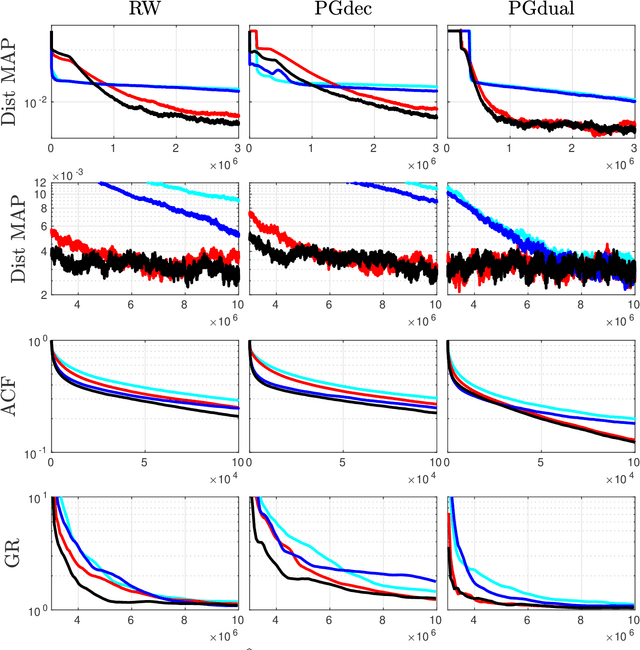
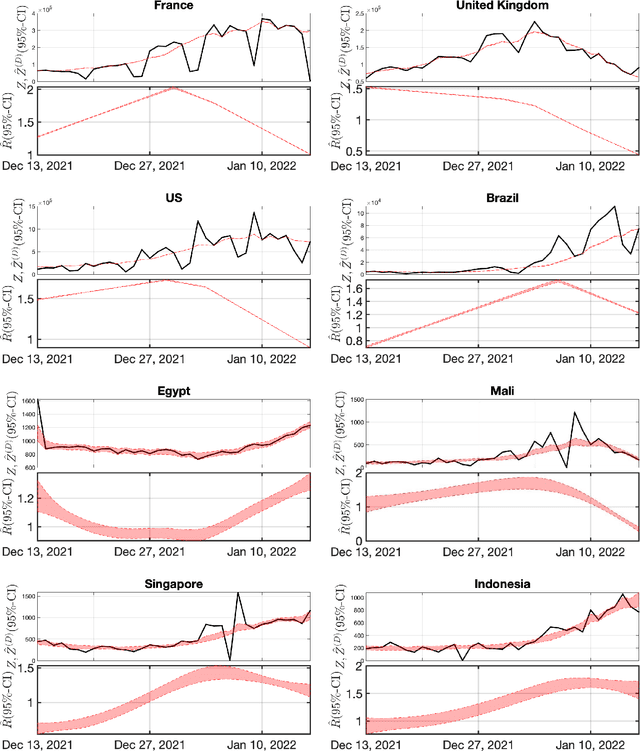
Monitoring the Covid19 pandemic constitutes a critical societal stake that received considerable research efforts. The intensity of the pandemic on a given territory is efficiently measured by the reproduction number, quantifying the rate of growth of daily new infections. Recently, estimates for the time evolution of the reproduction number were produced using an inverse problem formulation with a nonsmooth functional minimization. While it was designed to be robust to the limited quality of the Covid19 data (outliers, missing counts), the procedure lacks the ability to output credibility interval based estimates. This remains a severe limitation for practical use in actual pandemic monitoring by epidemiologists that the present work aims to overcome by use of Monte Carlo sampling. After interpretation of the functional into a Bayesian framework, several sampling schemes are tailored to adjust the nonsmooth nature of the resulting posterior distribution. The originality of the devised algorithms stems from combining a Langevin Monte Carlo sampling scheme with Proximal operators. Performance of the new algorithms in producing relevant credibility intervals for the reproduction number estimates and denoised counts are compared. Assessment is conducted on real daily new infection counts made available by the Johns Hopkins University. The interest of the devised monitoring tools are illustrated on Covid19 data from several different countries.

Federated Expectation Maximization with heterogeneity mitigation and variance reduction

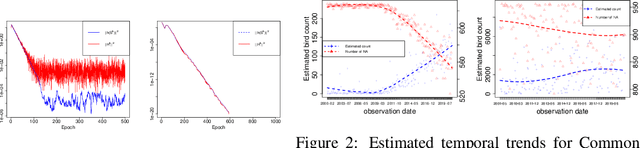
The Expectation Maximization (EM) algorithm is the default algorithm for inference in latent variable models. As in any other field of machine learning, applications of latent variable models to very large datasets make the use of advanced parallel and distributed architectures mandatory. This paper introduces FedEM, which is the first extension of the EM algorithm to the federated learning context. FedEM is a new communication efficient method, which handles partial participation of local devices, and is robust to heterogeneous distributions of the datasets. To alleviate the communication bottleneck, FedEM compresses appropriately defined complete data sufficient statistics. We also develop and analyze an extension of FedEM to further incorporate a variance reduction scheme. In all cases, we derive finite-time complexity bounds for smooth non-convex problems. Numerical results are presented to support our theoretical findings, as well as an application to federated missing values imputation for biodiversity monitoring.

The perturbed prox-preconditioned spider algorithm: non-asymptotic convergence bounds

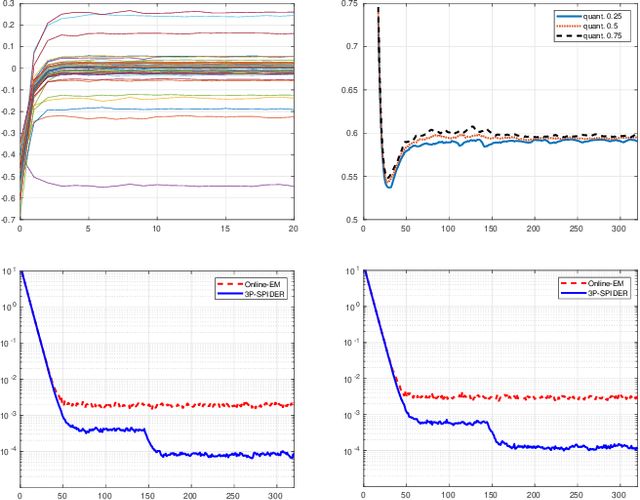
A novel algorithm named Perturbed Prox-Preconditioned SPIDER (3P-SPIDER) is introduced. It is a stochastic variancereduced proximal-gradient type algorithm built on Stochastic Path Integral Differential EstimatoR (SPIDER), an algorithm known to achieve near-optimal first-order oracle inequality for nonconvex and nonsmooth optimization. Compared to the vanilla prox-SPIDER, 3P-SPIDER uses preconditioned gradient estimators. Preconditioning can either be applied "explicitly" to a gradient estimator or be introduced "implicitly" as in applications to the EM algorithm. 3P-SPIDER also assumes that the preconditioned gradients may (possibly) be not known in closed analytical form and therefore must be approximated which adds an additional degree of perturbation. Studying the convergence in expectation, we show that 3P-SPIDER achieves a near-optimal oracle inequality O(n^(1/2) /epsilon) where n is the number of observations and epsilon the target precision even when the gradient is estimated by Monte Carlo methods. We illustrate the algorithm on an application to the minimization of a penalized empirical loss.

The Perturbed Prox-Preconditioned SPIDER algorithm for EM-based large scale learning

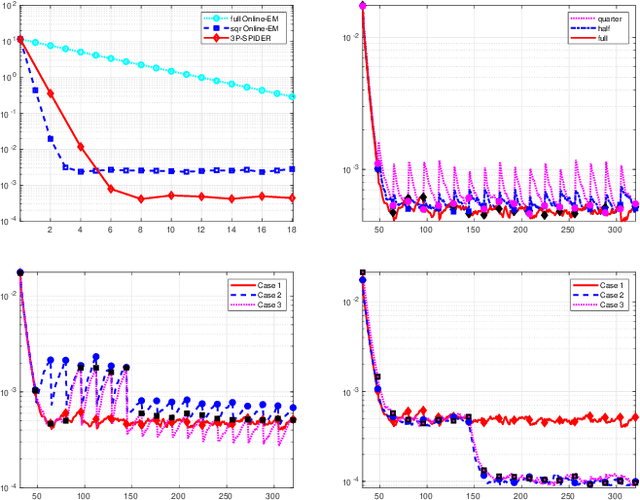
Incremental Expectation Maximization (EM) algorithms were introduced to design EM for the large scale learning framework by avoiding the full data set to be processed at each iteration. Nevertheless, these algorithms all assume that the conditional expectations of the sufficient statistics are explicit. In this paper, we propose a novel algorithm named Perturbed Prox-Preconditioned SPIDER (3P-SPIDER), which builds on the Stochastic Path Integral Differential EstimatoR EM (SPIDER-EM) algorithm. The 3P-SPIDER algorithm addresses many intractabilities of the E-step of EM; it also deals with non-smooth regularization and convex constraint set. Numerical experiments show that 3P-SPIDER outperforms other incremental EM methods and discuss the role of some design parameters.

Fast Incremental Expectation Maximization for finite-sum optimization: nonasymptotic convergence

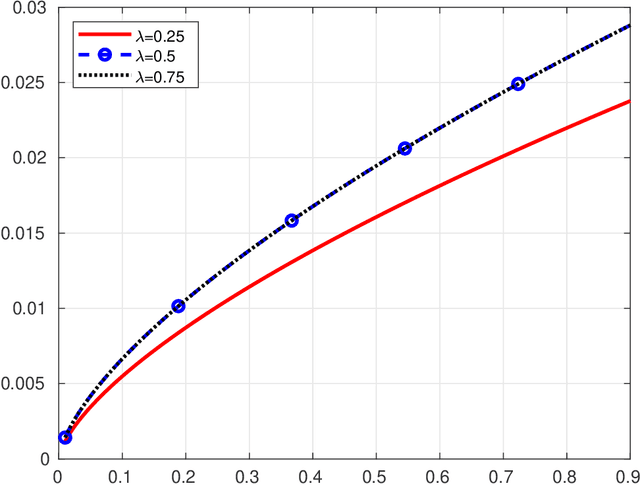
Fast Incremental Expectation Maximization (FIEM) is a version of the EM framework for large datasets. In this paper, we first recast FIEM and other incremental EM type algorithms in the {\em Stochastic Approximation within EM} framework. Then, we provide nonasymptotic bounds for the convergence in expectation as a function of the number of examples $n$ and of the maximal number of iterations $\kmax$. We propose two strategies for achieving an $\epsilon$-approximate stationary point, respectively with $\kmax = O(n^{2/3}/\epsilon)$ and $\kmax = O(\sqrt{n}/\epsilon^{3/2})$, both strategies relying on a random termination rule before $\kmax$ and on a constant step size in the Stochastic Approximation step. Our bounds provide some improvements on the literature. First, they allow $\kmax$ to scale as $\sqrt{n}$ which is better than $n^{2/3}$ which was the best rate obtained so far; it is at the cost of a larger dependence upon the tolerance $\epsilon$, thus making this control relevant for small to medium accuracy with respect to the number of examples $n$. Second, for the $n^{2/3}$-rate, the numerical illustrations show that thanks to an optimized choice of the step size and of the bounds in terms of quantities characterizing the optimization problem at hand, our results desig a less conservative choice of the step size and provide a better control of the convergence in expectation.

A Stochastic Path-Integrated Differential EstimatoR Expectation Maximization Algorithm

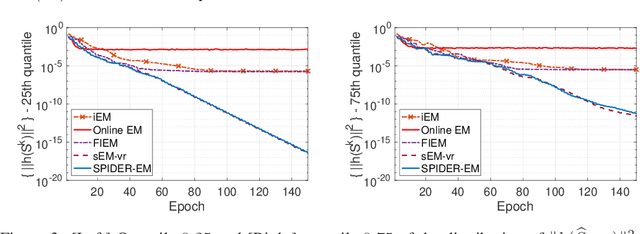
The Expectation Maximization (EM) algorithm is of key importance for inference in latent variable models including mixture of regressors and experts, missing observations. This paper introduces a novel EM algorithm, called \texttt{SPIDER-EM}, for inference from a training set of size $n$, $n \gg 1$. At the core of our algorithm is an estimator of the full conditional expectation in the {\sf E}-step, adapted from the stochastic path-integrated differential estimator ({\tt SPIDER}) technique. We derive finite-time complexity bounds for smooth non-convex likelihood: we show that for convergence to an $\epsilon$-approximate stationary point, the complexity scales as $K_{\operatorname{Opt}} (n,\epsilon )={\cal O}(\epsilon^{-1})$ and $K_{\operatorname{CE}}( n,\epsilon ) = n+ \sqrt{n} {\cal O}(\epsilon^{-1} )$, where $K_{\operatorname{Opt}}( n,\epsilon )$ and $K_{\operatorname{CE}}(n, \epsilon )$ are respectively the number of {\sf M}-steps and the number of per-sample conditional expectations evaluations. This improves over the state-of-the-art algorithms. Numerical results support our findings.

Geom-SPIDER-EM: Faster Variance Reduced Stochastic Expectation Maximization for Nonconvex Finite-Sum Optimization

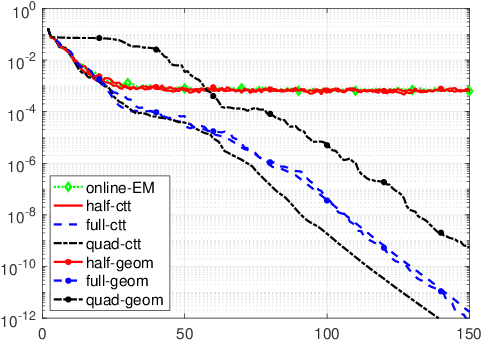
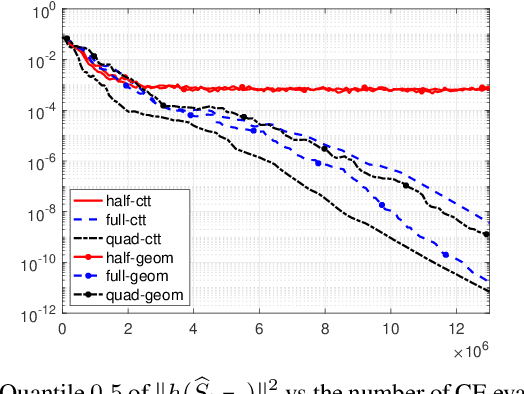
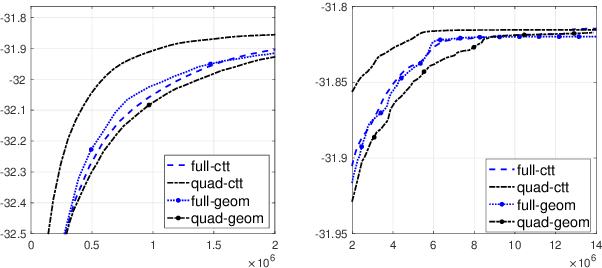
The Expectation Maximization (EM) algorithm is a key reference for inference in latent variable models; unfortunately, its computational cost is prohibitive in the large scale learning setting. In this paper, we propose an extension of the Stochastic Path-Integrated Differential EstimatoR EM (SPIDER-EM) and derive complexity bounds for this novel algorithm, designed to solve smooth nonconvex finite-sum optimization problems. We show that it reaches the same state of the art complexity bounds as SPIDER-EM; and provide conditions for a linear rate of convergence. Numerical results support our findings.