A Stochastic Path-Integrated Differential EstimatoR Expectation Maximization Algorithm
Paper and Code
Nov 30, 2020


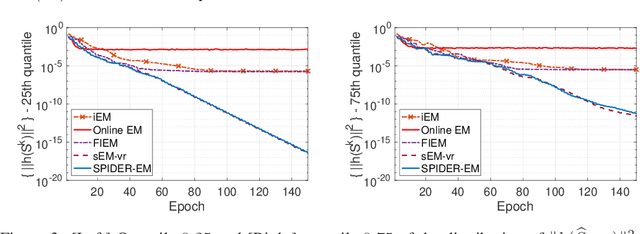
The Expectation Maximization (EM) algorithm is of key importance for inference in latent variable models including mixture of regressors and experts, missing observations. This paper introduces a novel EM algorithm, called \texttt{SPIDER-EM}, for inference from a training set of size $n$, $n \gg 1$. At the core of our algorithm is an estimator of the full conditional expectation in the {\sf E}-step, adapted from the stochastic path-integrated differential estimator ({\tt SPIDER}) technique. We derive finite-time complexity bounds for smooth non-convex likelihood: we show that for convergence to an $\epsilon$-approximate stationary point, the complexity scales as $K_{\operatorname{Opt}} (n,\epsilon )={\cal O}(\epsilon^{-1})$ and $K_{\operatorname{CE}}( n,\epsilon ) = n+ \sqrt{n} {\cal O}(\epsilon^{-1} )$, where $K_{\operatorname{Opt}}( n,\epsilon )$ and $K_{\operatorname{CE}}(n, \epsilon )$ are respectively the number of {\sf M}-steps and the number of per-sample conditional expectations evaluations. This improves over the state-of-the-art algorithms. Numerical results support our findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge