Distilling foundation models for robust and efficient models in digital pathology

In recent years, the advent of foundation models (FM) for digital pathology has relied heavily on scaling the pre-training datasets and the model size, yielding large and powerful models. While it resulted in improving the performance on diverse downstream tasks, it also introduced increased computational cost and inference time. In this work, we explore the distillation of a large foundation model into a smaller one, reducing the number of parameters by several orders of magnitude. Leveraging distillation techniques, our distilled model, H0-mini, achieves nearly comparable performance to large FMs at a significantly reduced inference cost. It is evaluated on several public benchmarks, achieving 3rd place on the HEST benchmark and 5th place on the EVA benchmark. Additionally, a robustness analysis conducted on the PLISM dataset demonstrates that our distilled model reaches excellent robustness to variations in staining and scanning conditions, significantly outperforming other state-of-the art models. This opens new perspectives to design lightweight and robust models for digital pathology, without compromising on performance.

Generative methods for sampling transition paths in molecular dynamics

Molecular systems often remain trapped for long times around some local minimum of the potential energy function, before switching to another one -- a behavior known as metastability. Simulating transition paths linking one metastable state to another one is difficult by direct numerical methods. In view of the promises of machine learning techniques, we explore in this work two approaches to more efficiently generate transition paths: sampling methods based on generative models such as variational autoencoders, and importance sampling methods based on reinforcement learning.

Inference of Multiscale Gaussian Graphical Model

Gaussian Graphical Models (GGMs) are widely used for exploratory data analysis in various fields such as genomics, ecology, psychometry. In a high-dimensional setting, when the number of variables exceeds the number of observations by several orders of magnitude, the estimation of GGM is a difficult and unstable optimization problem. Clustering of variables or variable selection is often performed prior to GGM estimation. We propose a new method allowing to simultaneously infer a hierarchical clustering structure and the graphs describing the structure of independence at each level of the hierarchy. This method is based on solving a convex optimization problem combining a graphical lasso penalty with a fused type lasso penalty. Results on real and synthetic data are presented.

Federated Expectation Maximization with heterogeneity mitigation and variance reduction

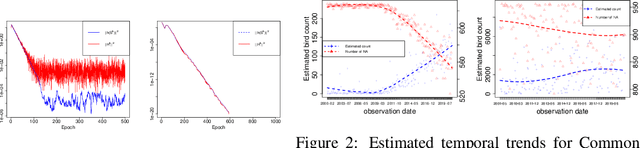
The Expectation Maximization (EM) algorithm is the default algorithm for inference in latent variable models. As in any other field of machine learning, applications of latent variable models to very large datasets make the use of advanced parallel and distributed architectures mandatory. This paper introduces FedEM, which is the first extension of the EM algorithm to the federated learning context. FedEM is a new communication efficient method, which handles partial participation of local devices, and is robust to heterogeneous distributions of the datasets. To alleviate the communication bottleneck, FedEM compresses appropriately defined complete data sufficient statistics. We also develop and analyze an extension of FedEM to further incorporate a variance reduction scheme. In all cases, we derive finite-time complexity bounds for smooth non-convex problems. Numerical results are presented to support our theoretical findings, as well as an application to federated missing values imputation for biodiversity monitoring.

Link Prediction in the Stochastic Block Model with Outliers

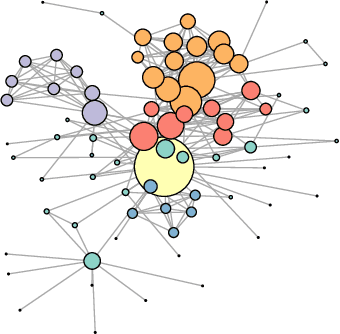
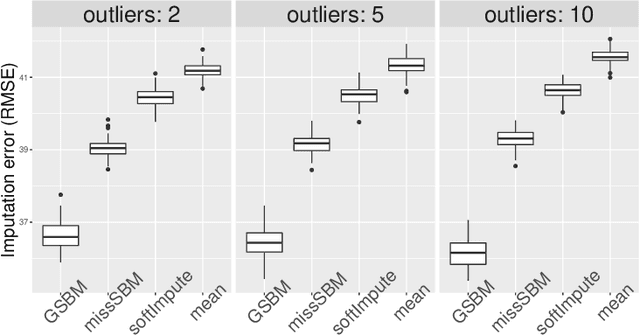
The Stochastic Block Model is a popular model for network analysis in the presence of community structure. However, in numerous examples, the assumptions underlying this classical model are put in default by the behaviour of a small number of outlier nodes such as hubs, nodes with mixed membership profiles, or corrupted nodes. In addition, real-life networks are likely to be incomplete, due to non-response or machine failures. We introduce a new algorithm to estimate the connection probabilities in a network, which is robust to both outlier nodes and missing observations. Under fairly general assumptions, this method detects the outliers, and achieves the best known error for the estimation of connection probabilities with polynomial computation cost. In addition, we prove sub-linear convergence of our algorithm. We provide a simulation study which demonstrates the good behaviour of the method in terms of outliers selection and prediction of the missing links.

Low-rank Interaction with Sparse Additive Effects Model for Large Data Frames

Many applications of machine learning involve the analysis of large data frames-matrices collecting heterogeneous measurements (binary, numerical, counts, etc.) across samples-with missing values. Low-rank models, as studied by Udell et al. [30], are popular in this framework for tasks such as visualization, clustering and missing value imputation. Yet, available methods with statistical guarantees and efficient optimization do not allow explicit modeling of main additive effects such as row and column, or covariate effects. In this paper, we introduce a low-rank interaction and sparse additive effects (LORIS) model which combines matrix regression on a dictionary and low-rank design, to estimate main effects and interactions simultaneously. We provide statistical guarantees in the form of upper bounds on the estimation error of both components. Then, we introduce a mixed coordinate gradient descent (MCGD) method which provably converges sub-linearly to an optimal solution and is computationally efficient for large scale data sets. We show on simulated and survey data that the method has a clear advantage over current practices, which consist in dealing separately with additive effects in a preprocessing step.