Principled Federated Random Forests for Heterogeneous Data

Random Forests (RF) are among the most powerful and widely used predictive models for centralized tabular data, yet few methods exist to adapt them to the federated learning setting. Unlike most federated learning approaches, the piecewise-constant nature of RF prevents exact gradient-based optimization. As a result, existing federated RF implementations rely on unprincipled heuristics: for instance, aggregating decision trees trained independently on clients fails to optimize the global impurity criterion, even under simple distribution shifts. We propose FedForest, a new federated RF algorithm for horizontally partitioned data that naturally accommodates diverse forms of client data heterogeneity, from covariate shift to more complex outcome shift mechanisms. We prove that our splitting procedure, based on aggregating carefully chosen client statistics, closely approximates the split selected by a centralized algorithm. Moreover, FedForest allows splits on client indicators, enabling a non-parametric form of personalization that is absent from prior federated random forest methods. Empirically, we demonstrate that the resulting federated forests closely match centralized performance across heterogeneous benchmarks while remaining communication-efficient.

Preference-based Conditional Treatment Effects and Policy Learning

We introduce a new preference-based framework for conditional treatment effect estimation and policy learning, built on the Conditional Preference-based Treatment Effect (CPTE). CPTE requires only that outcomes be ranked under a preference rule, unlocking flexible modeling of heterogeneous effects with multivariate, ordinal, or preference-driven outcomes. This unifies applications such as conditional probability of necessity and sufficiency, conditional Win Ratio, and Generalized Pairwise Comparisons. Despite the intrinsic non-identifiability of comparison-based estimands, CPTE provides interpretable targets and delivers new identifiability conditions for previous unidentifiable estimands. We present estimation strategies via matching, quantile, and distributional regression, and further design efficient influence-function estimators to correct plug-in bias and maximize policy value. Synthetic and semi-synthetic experiments demonstrate clear performance gains and practical impact.

Membership Inference Attacks from Causal Principles

Membership Inference Attacks (MIAs) are widely used to quantify training data memorization and assess privacy risks. Standard evaluation requires repeated retraining, which is computationally costly for large models. One-run methods (single training with randomized data inclusion) and zero-run methods (post hoc evaluation) are often used instead, though their statistical validity remains unclear. To address this gap, we frame MIA evaluation as a causal inference problem, defining memorization as the causal effect of including a data point in the training set. This novel formulation reveals and formalizes key sources of bias in existing protocols: one-run methods suffer from interference between jointly included points, while zero-run evaluations popular for LLMs are confounded by non-random membership assignment. We derive causal analogues of standard MIA metrics and propose practical estimators for multi-run, one-run, and zero-run regimes with non-asymptotic consistency guarantees. Experiments on real-world data show that our approach enables reliable memorization measurement even when retraining is impractical and under distribution shift, providing a principled foundation for privacy evaluation in modern AI systems.

When Pattern-by-Pattern Works: Theoretical and Empirical Insights for Logistic Models with Missing Values

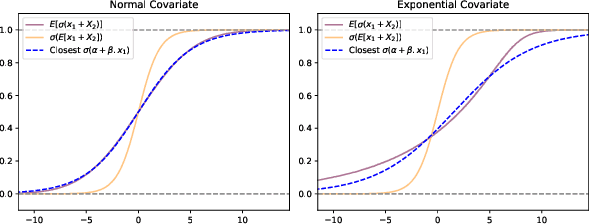
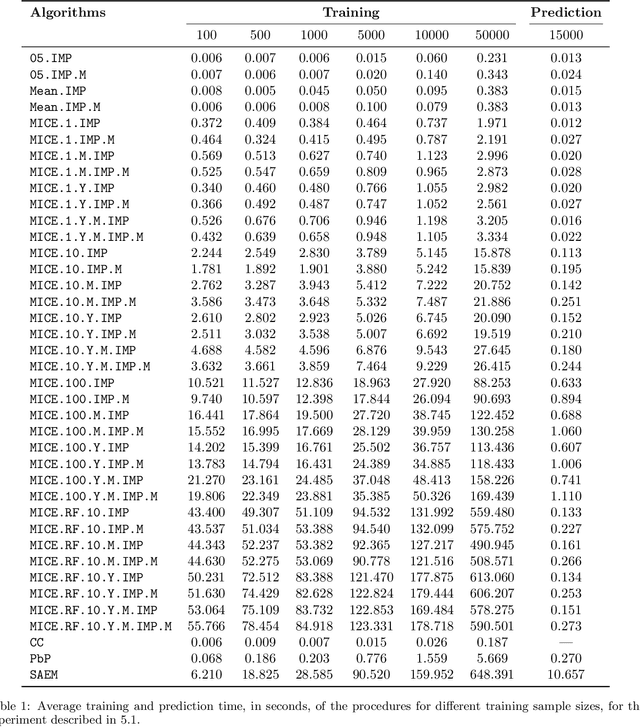
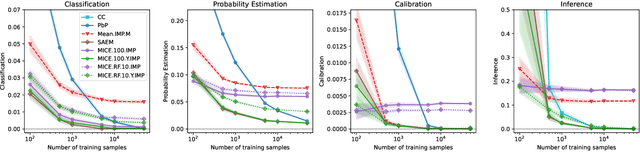
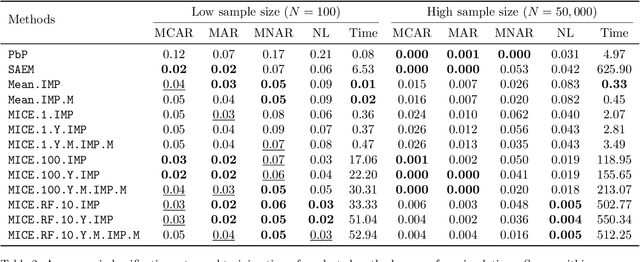
Predicting a response with partially missing inputs remains a challenging task even in parametric models, since parameter estimation in itself is not sufficient to predict on partially observed inputs. Several works study prediction in linear models. In this paper, we focus on logistic models, which present their own difficulties. From a theoretical perspective, we prove that a Pattern-by-Pattern strategy (PbP), which learns one logistic model per missingness pattern, accurately approximates Bayes probabilities in various missing data scenarios (MCAR, MAR and MNAR). Empirically, we thoroughly compare various methods (constant and iterative imputations, complete case analysis, PbP, and an EM algorithm) across classification, probability estimation, calibration, and parameter inference. Our analysis provides a comprehensive view on the logistic regression with missing values. It reveals that mean imputation can be used as baseline for low sample sizes, and improved performance is obtained via nonlinear multiple iterative imputation techniques with the labels (MICE.RF.Y). For large sample sizes, PbP is the best method for Gaussian mixtures, and we recommend MICE.RF.Y in presence of nonlinear features.

Model Agnostic Differentially Private Causal Inference

Estimating causal effects from observational data is essential in fields such as medicine, economics and social sciences, where privacy concerns are paramount. We propose a general, model-agnostic framework for differentially private estimation of average treatment effects (ATE) that avoids strong structural assumptions on the data-generating process or the models used to estimate propensity scores and conditional outcomes. In contrast to prior work, which enforces differential privacy by directly privatizing these nuisance components and results in a privacy cost that scales with model complexity, our approach decouples nuisance estimation from privacy protection. This separation allows the use of flexible, state-of-the-art black-box models, while differential privacy is achieved by perturbing only predictions and aggregation steps within a fold-splitting scheme with ensemble techniques. We instantiate the framework for three classical estimators -- the G-formula, inverse propensity weighting (IPW), and augmented IPW (AIPW) -- and provide formal utility and privacy guarantees. Empirical results show that our methods maintain competitive performance under realistic privacy budgets. We further extend our framework to support meta-analysis of multiple private ATE estimates. Our results bridge a critical gap between causal inference and privacy-preserving data analysis.

Optimal Transport with Heterogeneously Missing Data

We consider the problem of solving the optimal transport problem between two empirical distributions with missing values. Our main assumption is that the data is missing completely at random (MCAR), but we allow for heterogeneous missingness probabilities across features and across the two distributions. As a first contribution, we show that the Wasserstein distance between empirical Gaussian distributions and linear Monge maps between arbitrary distributions can be debiased without significantly affecting the sample complexity. Secondly, we show that entropic regularized optimal transport can be estimated efficiently and consistently using iterative singular value thresholding (ISVT). We propose a validation set-free hyperparameter selection strategy for ISVT that leverages our estimator of the Bures-Wasserstein distance, which could be of independent interest in general matrix completion problems. Finally, we validate our findings on a wide range of numerical applications.

Causal mediation analysis with one or multiple mediators: a comparative study

Mediation analysis breaks down the causal effect of a treatment on an outcome into an indirect effect, acting through a third group of variables called mediators, and a direct effect, operating through other mechanisms. Mediation analysis is hard because confounders between treatment, mediators, and outcome blur effect estimates in observational studies. Many estimators have been proposed to adjust on those confounders and provide accurate causal estimates. We consider parametric and non-parametric implementations of classical estimators and provide a thorough evaluation for the estimation of the direct and indirect effects in the context of causal mediation analysis for binary, continuous, and multi-dimensional mediators. We assess several approaches in a comprehensive benchmark on simulated data. Our results show that advanced statistical approaches such as the multiply robust and the double machine learning estimators achieve good performances in most of the simulated settings and on real data. As an example of application, we propose a thorough analysis of factors known to influence cognitive functions to assess if the mechanism involves modifications in brain morphology using the UK Biobank brain imaging cohort. This analysis shows that for several physiological factors, such as hypertension and obesity, a substantial part of the effect is mediated by changes in the brain structure. This work provides guidance to the practitioner from the formulation of a valid causal mediation problem, including the verification of the identification assumptions, to the choice of an adequate estimator.

Expert Study on Interpretable Machine Learning Models with Missing Data

Inherently interpretable machine learning (IML) models provide valuable insights for clinical decision-making but face challenges when features have missing values. Classical solutions like imputation or excluding incomplete records are often unsuitable in applications where values are missing at test time. In this work, we conducted a survey with 71 clinicians from 29 trauma centers across France, including 20 complete responses to study the interaction between medical professionals and IML applied to data with missing values. This provided valuable insights into how missing data is interpreted in clinical machine learning. We used the prediction of hemorrhagic shock as a concrete example to gauge the willingness and readiness of the participants to adopt IML models from three classes of methods. Our findings show that, while clinicians value interpretability and are familiar with common IML methods, classical imputation techniques often misalign with their intuition, and that models that natively handle missing values are preferred. These results emphasize the need to integrate clinical intuition into future IML models for better human-computer interaction.

Federated Causal Inference: Multi-Centric ATE Estimation beyond Meta-Analysis

We study Federated Causal Inference, an approach to estimate treatment effects from decentralized data across centers. We compare three classes of Average Treatment Effect (ATE) estimators derived from the Plug-in G-Formula, ranging from simple meta-analysis to one-shot and multi-shot federated learning, the latter leveraging the full data to learn the outcome model (albeit requiring more communication). Focusing on Randomized Controlled Trials (RCTs), we derive the asymptotic variance of these estimators for linear models. Our results provide practical guidance on selecting the appropriate estimator for various scenarios, including heterogeneity in sample sizes, covariate distributions, treatment assignment schemes, and center effects. We validate these findings with a simulation study.

MMD-based Variable Importance for Distributional Random Forest

Distributional Random Forest (DRF) is a flexible forest-based method to estimate the full conditional distribution of a multivariate output of interest given input variables. In this article, we introduce a variable importance algorithm for DRFs, based on the well-established drop and relearn principle and MMD distance. While traditional importance measures only detect variables with an influence on the output mean, our algorithm detects variables impacting the output distribution more generally. We show that the introduced importance measure is consistent, exhibits high empirical performance on both real and simulated data, and outperforms competitors. In particular, our algorithm is highly efficient to select variables through recursive feature elimination, and can therefore provide small sets of variables to build accurate estimates of conditional output distributions.