Positivity-free Policy Learning with Observational Data

Policy learning utilizing observational data is pivotal across various domains, with the objective of learning the optimal treatment assignment policy while adhering to specific constraints such as fairness, budget, and simplicity. This study introduces a novel positivity-free (stochastic) policy learning framework designed to address the challenges posed by the impracticality of the positivity assumption in real-world scenarios. This framework leverages incremental propensity score policies to adjust propensity score values instead of assigning fixed values to treatments. We characterize these incremental propensity score policies and establish identification conditions, employing semiparametric efficiency theory to propose efficient estimators capable of achieving rapid convergence rates, even when integrated with advanced machine learning algorithms. This paper provides a thorough exploration of the theoretical guarantees associated with policy learning and validates the proposed framework's finite-sample performance through comprehensive numerical experiments, ensuring the identification of causal effects from observational data is both robust and reliable.

Simple Sorting Criteria Help Find the Causal Order in Additive Noise Models

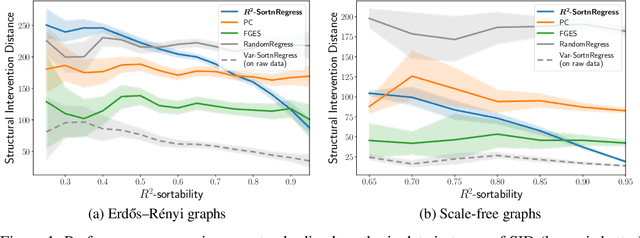
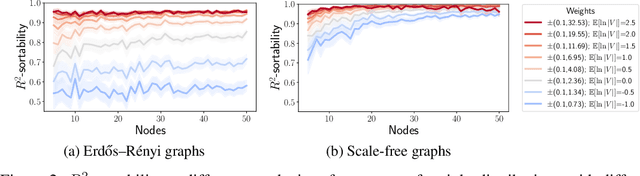
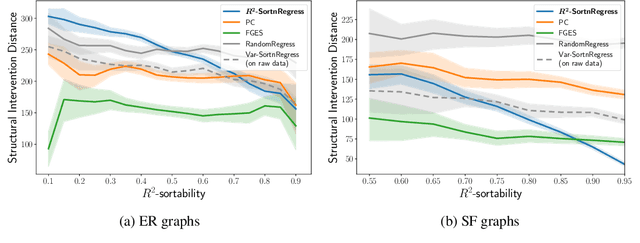
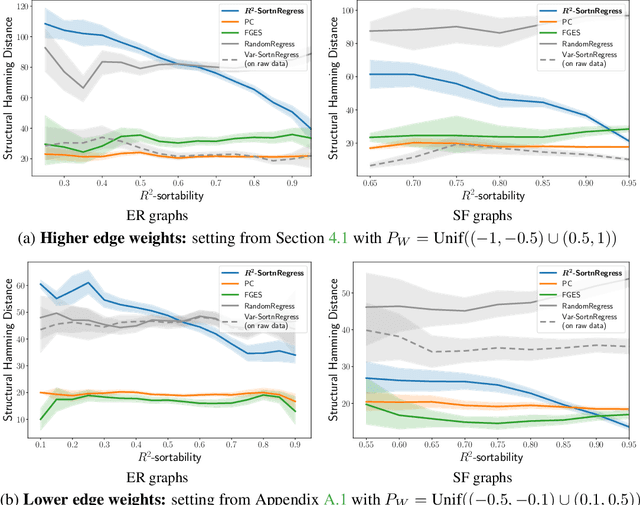
Additive Noise Models (ANM) encode a popular functional assumption that enables learning causal structure from observational data. Due to a lack of real-world data meeting the assumptions, synthetic ANM data are often used to evaluate causal discovery algorithms. Reisach et al. (2021) show that, for common simulation parameters, a variable ordering by increasing variance is closely aligned with a causal order and introduce var-sortability to quantify the alignment. Here, we show that not only variance, but also the fraction of a variable's variance explained by all others, as captured by the coefficient of determination $R^2$, tends to increase along the causal order. Simple baseline algorithms can use $R^2$-sortability to match the performance of established methods. Since $R^2$-sortability is invariant under data rescaling, these algorithms perform equally well on standardized or rescaled data, addressing a key limitation of algorithms exploiting var-sortability. We characterize and empirically assess $R^2$-sortability for different simulation parameters. We show that all simulation parameters can affect $R^2$-sortability and must be chosen deliberately to control the difficulty of the causal discovery task and the real-world plausibility of the simulated data. We provide an implementation of the sortability measures and sortability-based algorithms in our library CausalDisco (https://github.com/CausalDisco/CausalDisco).

Personalized Online Machine Learning

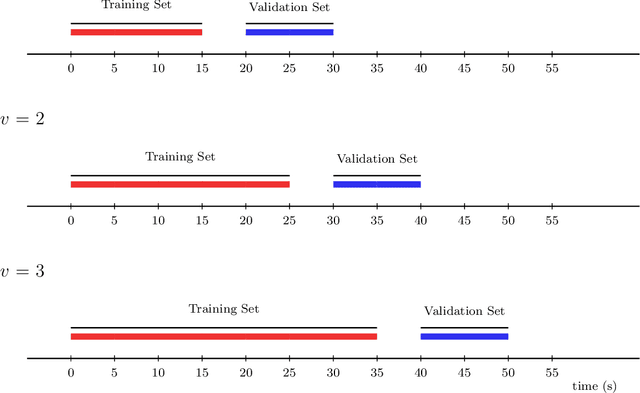
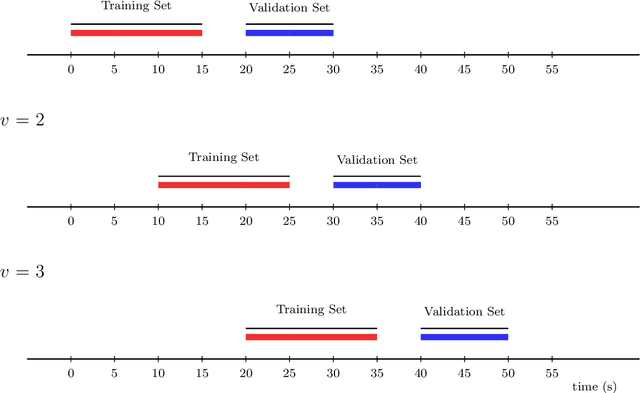
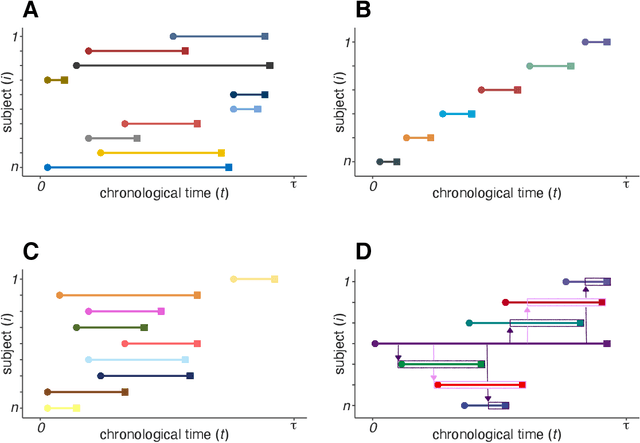
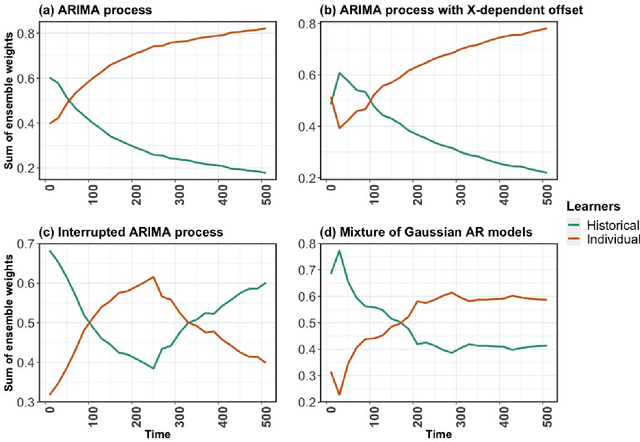
In this work, we introduce the Personalized Online Super Learner (POSL) -- an online ensembling algorithm for streaming data whose optimization procedure accommodates varying degrees of personalization. Namely, POSL optimizes predictions with respect to baseline covariates, so personalization can vary from completely individualized (i.e., optimization with respect to baseline covariate subject ID) to many individuals (i.e., optimization with respect to common baseline covariates). As an online algorithm, POSL learns in real-time. POSL can leverage a diversity of candidate algorithms, including online algorithms with different training and update times, fixed algorithms that are never updated during the procedure, pooled algorithms that learn from many individuals' time-series, and individualized algorithms that learn from within a single time-series. POSL's ensembling of this hybrid of base learning strategies depends on the amount of data collected, the stationarity of the time-series, and the mutual characteristics of a group of time-series. In essence, POSL decides whether to learn across samples, through time, or both, based on the underlying (unknown) structure in the data. For a wide range of simulations that reflect realistic forecasting scenarios, and in a medical data application, we examine the performance of POSL relative to other current ensembling and online learning methods. We show that POSL is able to provide reliable predictions for time-series data and adjust to changing data-generating environments. We further cultivate POSL's practicality by extending it to settings where time-series enter/exit dynamically over chronological time.

Risk Minimization from Adaptively Collected Data: Guarantees for Supervised and Policy Learning

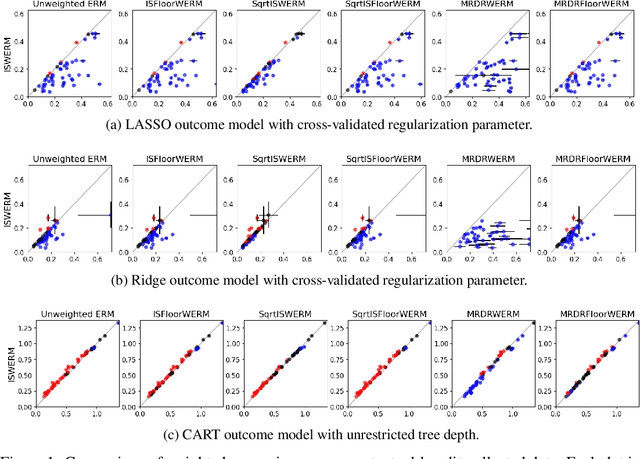
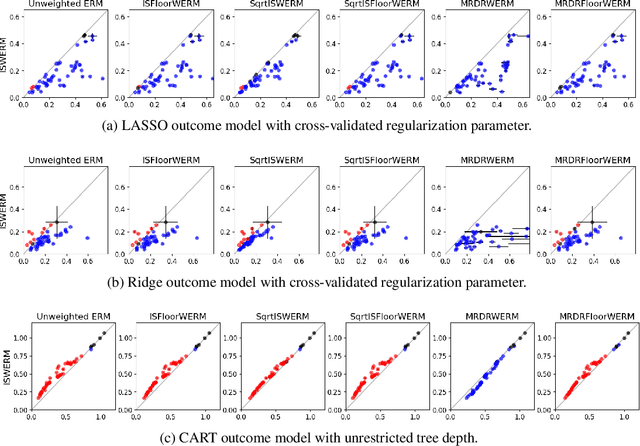
Empirical risk minimization (ERM) is the workhorse of machine learning, whether for classification and regression or for off-policy policy learning, but its model-agnostic guarantees can fail when we use adaptively collected data, such as the result of running a contextual bandit algorithm. We study a generic importance sampling weighted ERM algorithm for using adaptively collected data to minimize the average of a loss function over a hypothesis class and provide first-of-their-kind generalization guarantees and fast convergence rates. Our results are based on a new maximal inequality that carefully leverages the importance sampling structure to obtain rates with the right dependence on the exploration rate in the data. For regression, we provide fast rates that leverage the strong convexity of squared-error loss. For policy learning, we provide rate-optimal regret guarantees that close an open gap in the existing literature whenever exploration decays to zero, as is the case for bandit-collected data. An empirical investigation validates our theory.

Post-Contextual-Bandit Inference

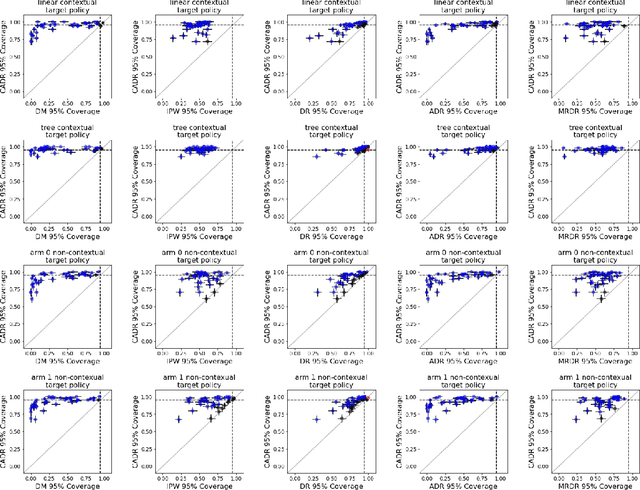
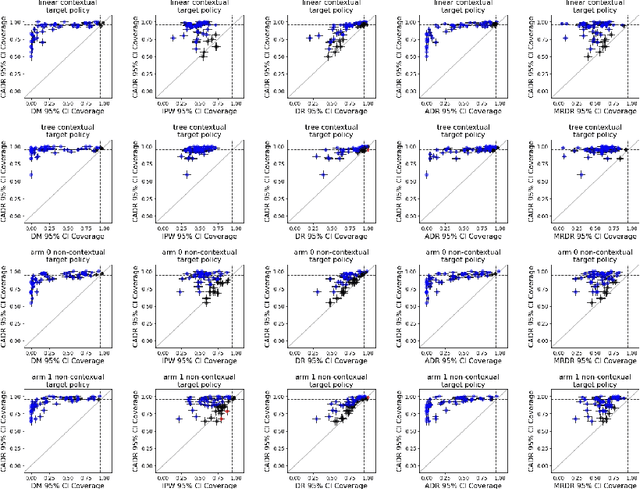
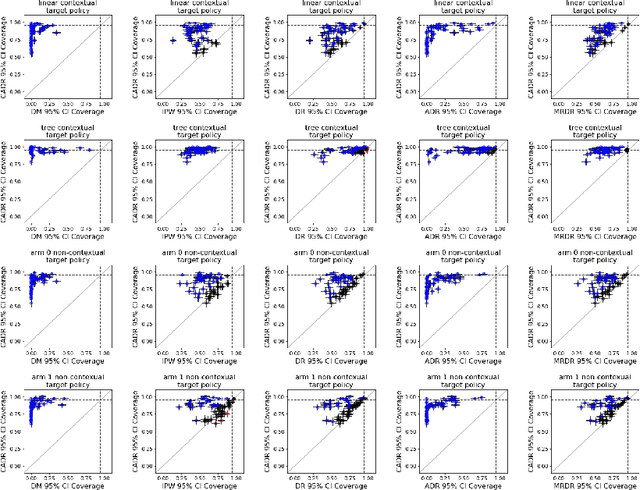
Contextual bandit algorithms are increasingly replacing non-adaptive A/B tests in e-commerce, healthcare, and policymaking because they can both improve outcomes for study participants and increase the chance of identifying good or even best policies. To support credible inference on novel interventions at the end of the study, nonetheless, we still want to construct valid confidence intervals on average treatment effects, subgroup effects, or value of new policies. The adaptive nature of the data collected by contextual bandit algorithms, however, makes this difficult: standard estimators are no longer asymptotically normally distributed and classic confidence intervals fail to provide correct coverage. While this has been addressed in non-contextual settings by using stabilized estimators, the contextual setting poses unique challenges that we tackle for the first time in this paper. We propose the Contextual Adaptive Doubly Robust (CADR) estimator, the first estimator for policy value that is asymptotically normal under contextual adaptive data collection. The main technical challenge in constructing CADR is designing adaptive and consistent conditional standard deviation estimators for stabilization. Extensive numerical experiments using 57 OpenML datasets demonstrate that confidence intervals based on CADR uniquely provide correct coverage.

Rate-adaptive model selection over a collection of black-box contextual bandit algorithms

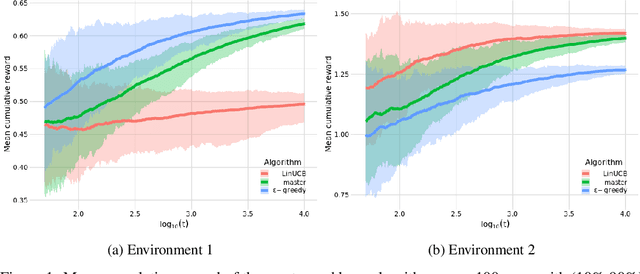
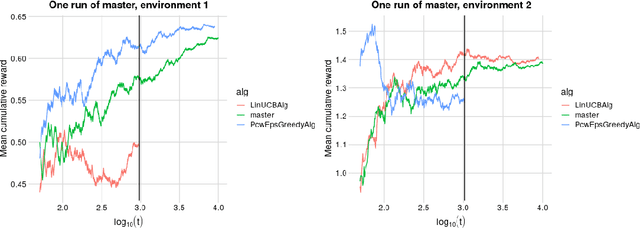
We consider the model selection task in the stochastic contextual bandit setting. Suppose we are given a collection of base contextual bandit algorithms. We provide a master algorithm that combines them and achieves the same performance, up to constants, as the best base algorithm would, if it had been run on its own. Our approach only requires that each algorithm satisfy a high probability regret bound. Our procedure is very simple and essentially does the following: for a well chosen sequence of probabilities $(p_{t})_{t\geq 1}$, at each round $t$, it either chooses at random which candidate to follow (with probability $p_{t}$) or compares, at the same internal sample size for each candidate, the cumulative reward of each, and selects the one that wins the comparison (with probability $1-p_{t}$). To the best of our knowledge, our proposal is the first one to be rate-adaptive for a collection of general black-box contextual bandit algorithms: it achieves the same regret rate as the best candidate. We demonstrate the effectiveness of our method with simulation studies.

Generalized Policy Elimination: an efficient algorithm for Nonparametric Contextual Bandits

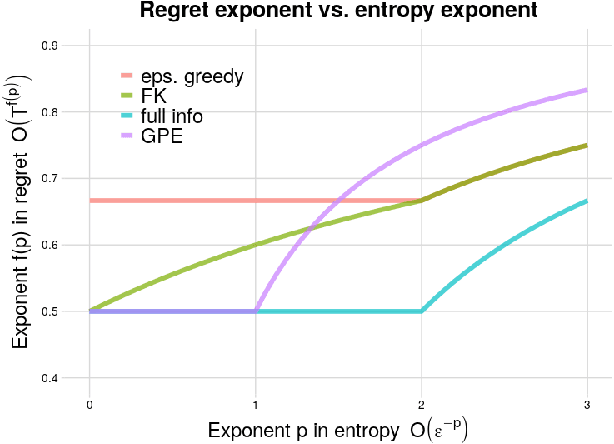
We propose the Generalized Policy Elimination (GPE) algorithm, an oracle-efficient contextual bandit (CB) algorithm inspired by the Policy Elimination algorithm of \cite{dudik2011}. We prove the first regret optimality guarantee theorem for an oracle-efficient CB algorithm competing against a nonparametric class with infinite VC-dimension. Specifically, we show that GPE is regret-optimal (up to logarithmic factors) for policy classes with integrable entropy. For classes with larger entropy, we show that the core techniques used to analyze GPE can be used to design an $\varepsilon$-greedy algorithm with regret bound matching that of the best algorithms to date. We illustrate the applicability of our algorithms and theorems with examples of large nonparametric policy classes, for which the relevant optimization oracles can be efficiently implemented.

Collaborative targeted inference from continuously indexed nuisance parameter estimators

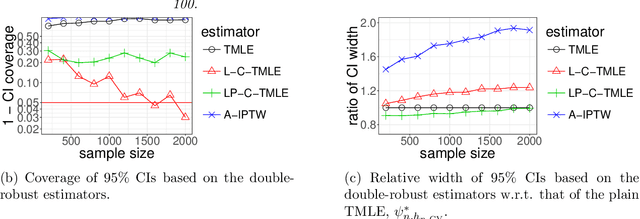
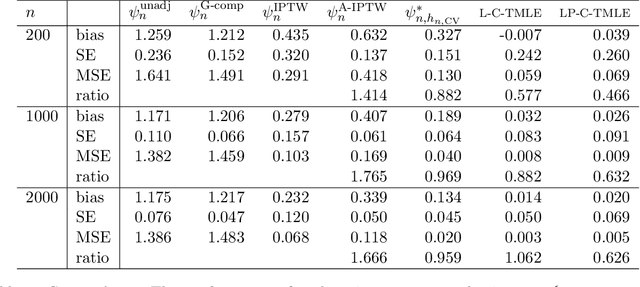
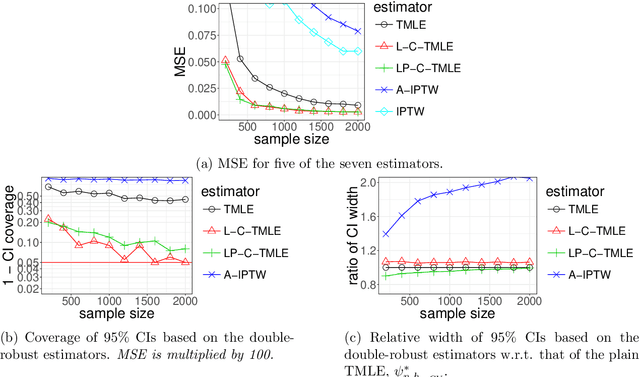
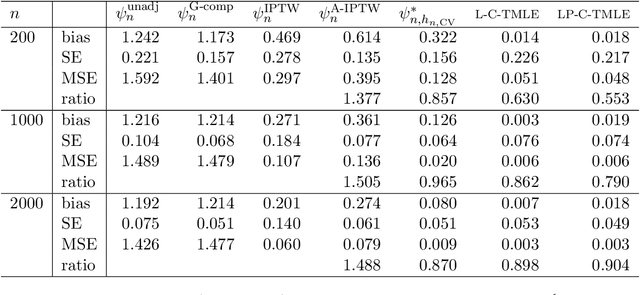
We wish to infer the value of a parameter at a law from which we sample independent observations. The parameter is smooth and we can define two variation-independent features of the law, its $Q$- and $G$-components, such that estimating them consistently at a fast enough product of rates allows to build a confidence interval (CI) with a given asymptotic level from a plain targeted minimum loss estimator (TMLE). Say that the above product is not fast enough and the algorithm for the $G$-component is fine-tuned by a real-valued $h$. A plain TMLE with an $h$ chosen by cross-validation would typically not yield a CI. We construct a collaborative TMLE (C-TMLE) and show under mild conditions that, if there exists an oracle $h$ that makes a bulky remainder term asymptotically Gaussian, then the C-TMLE yields a CI. We illustrate our findings with the inference of the average treatment effect. We conduct a simulation study where the $G$-component is estimated by the LASSO and $h$ is the bound on the coefficients' norms. It sheds light on small sample properties, in the face of low- to high-dimensional baseline covariates, and possibly positivity violation.

Asymptotically Optimal Algorithms for Budgeted Multiple Play Bandits

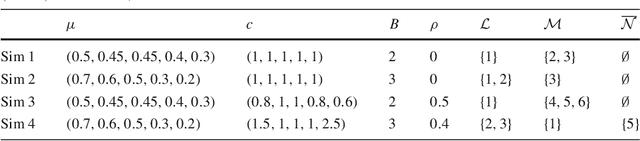
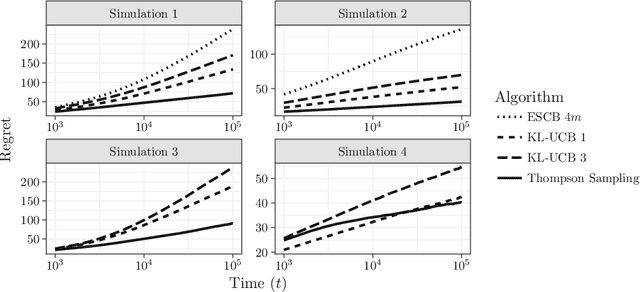
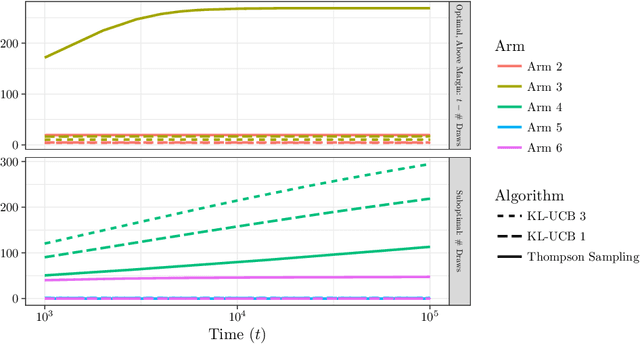
We study a generalization of the multi-armed bandit problem with multiple plays where there is a cost associated with pulling each arm and the agent has a budget at each time that dictates how much she can expect to spend. We derive an asymptotic regret lower bound for any uniformly efficient algorithm in our setting. We then study a variant of Thompson sampling for Bernoulli rewards and a variant of KL-UCB for both single-parameter exponential families and bounded, finitely supported rewards. We show these algorithms are asymptotically optimal, both in rate and leading problem-dependent constants, including in the thick margin setting where multiple arms fall on the decision boundary.