Nonparametric Instrumental Variable Inference with Many Weak Instruments

We study inference on linear functionals in the nonparametric instrumental variable (NPIV) problem with a discretely-valued instrument under a many-weak-instruments asymptotic regime, where the number of instrument values grows with the sample size. A key motivating example is estimating long-term causal effects in a new experiment with only short-term outcomes, using past experiments to instrument for the effect of short- on long-term outcomes. Here, the assignment to a past experiment serves as the instrument: we have many past experiments but only a limited number of units in each. Since the structural function is nonparametric but constrained by only finitely many moment restrictions, point identification typically fails. To address this, we consider linear functionals of the minimum-norm solution to the moment restrictions, which is always well-defined. As the number of instrument levels grows, these functionals define an approximating sequence to a target functional, replacing point identification with a weaker asymptotic notion suited to discrete instruments. Extending the Jackknife Instrumental Variable Estimator (JIVE) beyond the classical parametric setting, we propose npJIVE, a nonparametric estimator for solutions to linear inverse problems with many weak instruments. We construct automatic debiased machine learning estimators for linear functionals of both the structural function and its minimum-norm projection, and establish their efficiency in the many-weak-instruments regime.

Automatic Double Reinforcement Learning in Semiparametric Markov Decision Processes with Applications to Long-Term Causal Inference

Double reinforcement learning (DRL) enables statistically efficient inference on the value of a policy in a nonparametric Markov Decision Process (MDP) given trajectories generated by another policy. However, this approach necessarily requires stringent overlap between the state distributions, which is often violated in practice. To relax this requirement and extend DRL, we study efficient inference on linear functionals of the $Q$-function (of which policy value is a special case) in infinite-horizon, time-invariant MDPs under semiparametric restrictions on the $Q$-function. These restrictions can reduce the overlap requirement and lower the efficiency bound, yielding more precise estimates. As an important example, we study the evaluation of long-term value under domain adaptation, given a few short trajectories from the new domain and restrictions on the difference between the domains. This can be used for long-term causal inference. Our method combines flexible estimates of the $Q$-function and the Riesz representer of the functional of interest (e.g., the stationary state density ratio for policy value) and is automatic in that we do not need to know the form of the latter - only the functional we care about. To address potential model misspecification bias, we extend the adaptive debiased machine learning (ADML) framework of \citet{van2023adaptive} to construct nonparametrically valid and superefficient estimators that adapt to the functional form of the $Q$-function. As a special case, we propose a novel adaptive debiased plug-in estimator that uses isotonic-calibrated fitted $Q$-iteration - a new calibration algorithm for MDPs - to circumvent the computational challenges of estimating debiasing nuisances from min-max objectives.

Demistifying Inference after Adaptive Experiments

Adaptive experiments such as multi-arm bandits adapt the treatment-allocation policy and/or the decision to stop the experiment to the data observed so far. This has the potential to improve outcomes for study participants within the experiment, to improve the chance of identifying best treatments after the experiment, and to avoid wasting data. Seen as an experiment (rather than just a continually optimizing system) it is still desirable to draw statistical inferences with frequentist guarantees. The concentration inequalities and union bounds that generally underlie adaptive experimentation algorithms can yield overly conservative inferences, but at the same time the asymptotic normality we would usually appeal to in non-adaptive settings can be imperiled by adaptivity. In this article we aim to explain why, how, and when adaptivity is in fact an issue for inference and, when it is, understand the various ways to fix it: reweighting to stabilize variances and recover asymptotic normality, always-valid inference based on joint normality of an asymptotic limiting sequence, and characterizing and inverting the non-normal distributions induced by adaptivity.

Risk Minimization from Adaptively Collected Data: Guarantees for Supervised and Policy Learning

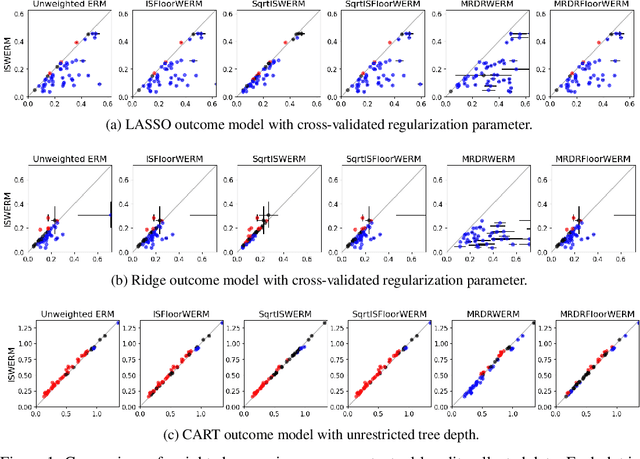
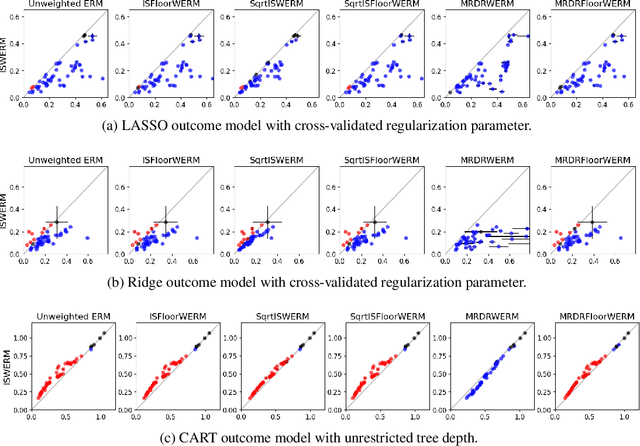
Empirical risk minimization (ERM) is the workhorse of machine learning, whether for classification and regression or for off-policy policy learning, but its model-agnostic guarantees can fail when we use adaptively collected data, such as the result of running a contextual bandit algorithm. We study a generic importance sampling weighted ERM algorithm for using adaptively collected data to minimize the average of a loss function over a hypothesis class and provide first-of-their-kind generalization guarantees and fast convergence rates. Our results are based on a new maximal inequality that carefully leverages the importance sampling structure to obtain rates with the right dependence on the exploration rate in the data. For regression, we provide fast rates that leverage the strong convexity of squared-error loss. For policy learning, we provide rate-optimal regret guarantees that close an open gap in the existing literature whenever exploration decays to zero, as is the case for bandit-collected data. An empirical investigation validates our theory.

Post-Contextual-Bandit Inference

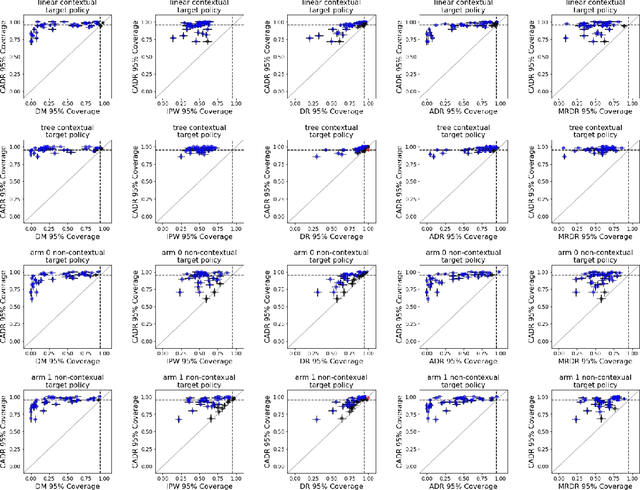
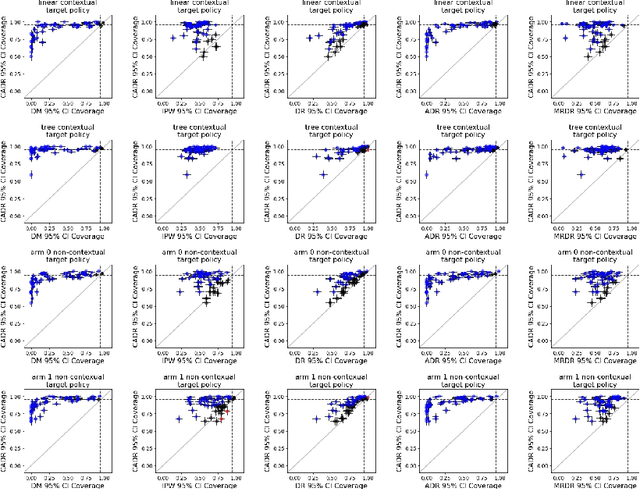
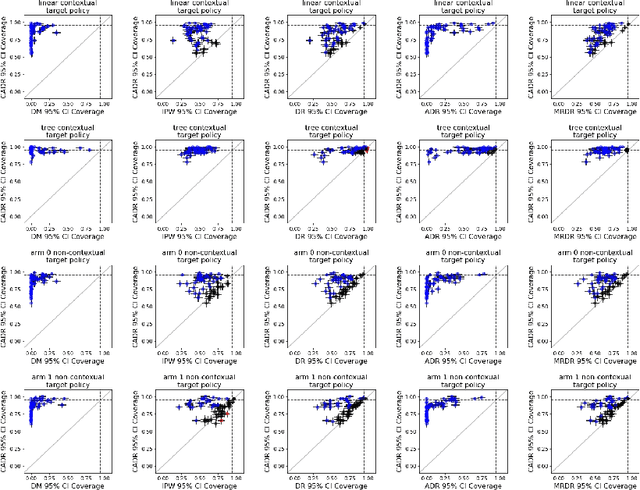
Contextual bandit algorithms are increasingly replacing non-adaptive A/B tests in e-commerce, healthcare, and policymaking because they can both improve outcomes for study participants and increase the chance of identifying good or even best policies. To support credible inference on novel interventions at the end of the study, nonetheless, we still want to construct valid confidence intervals on average treatment effects, subgroup effects, or value of new policies. The adaptive nature of the data collected by contextual bandit algorithms, however, makes this difficult: standard estimators are no longer asymptotically normally distributed and classic confidence intervals fail to provide correct coverage. While this has been addressed in non-contextual settings by using stabilized estimators, the contextual setting poses unique challenges that we tackle for the first time in this paper. We propose the Contextual Adaptive Doubly Robust (CADR) estimator, the first estimator for policy value that is asymptotically normal under contextual adaptive data collection. The main technical challenge in constructing CADR is designing adaptive and consistent conditional standard deviation estimators for stabilization. Extensive numerical experiments using 57 OpenML datasets demonstrate that confidence intervals based on CADR uniquely provide correct coverage.

The Relative Performance of Ensemble Methods with Deep Convolutional Neural Networks for Image Classification

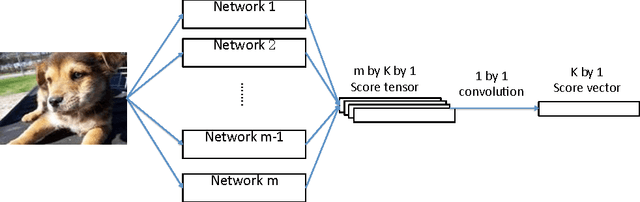
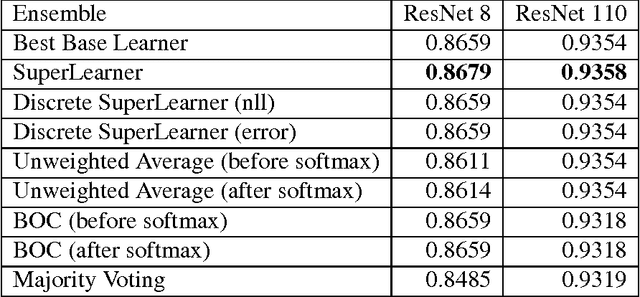
Artificial neural networks have been successfully applied to a variety of machine learning tasks, including image recognition, semantic segmentation, and machine translation. However, few studies fully investigated ensembles of artificial neural networks. In this work, we investigated multiple widely used ensemble methods, including unweighted averaging, majority voting, the Bayes Optimal Classifier, and the (discrete) Super Learner, for image recognition tasks, with deep neural networks as candidate algorithms. We designed several experiments, with the candidate algorithms being the same network structure with different model checkpoints within a single training process, networks with same structure but trained multiple times stochastically, and networks with different structure. In addition, we further studied the over-confidence phenomenon of the neural networks, as well as its impact on the ensemble methods. Across all of our experiments, the Super Learner achieved best performance among all the ensemble methods in this study.