Hybrid Meta-learners for Estimating Heterogeneous Treatment Effects

Estimating conditional average treatment effects (CATE) from observational data involves modeling decisions that differ from supervised learning, particularly concerning how to regularize model complexity. Previous approaches can be grouped into two primary "meta-learner" paradigms that impose distinct inductive biases. Indirect meta-learners first fit and regularize separate potential outcome (PO) models and then estimate CATE by taking their difference, whereas direct meta-learners construct and directly regularize estimators for the CATE function itself. Neither approach consistently outperforms the other across all scenarios: indirect learners perform well when the PO functions are simple, while direct learners outperform when the CATE is simpler than individual PO functions. In this paper, we introduce the Hybrid Learner (H-learner), a novel regularization strategy that interpolates between the direct and indirect regularizations depending on the dataset at hand. The H-learner achieves this by learning intermediate functions whose difference closely approximates the CATE without necessarily requiring accurate individual approximations of the POs themselves. We demonstrate empirically that intentionally allowing suboptimal fits to the POs improves the bias-variance tradeoff in estimating CATE. Experiments conducted on semi-synthetic and real-world benchmark datasets illustrate that the H-learner consistently operates at the Pareto frontier, effectively combining the strengths of both direct and indirect meta-learners.

Nonparametric Instrumental Variable Inference with Many Weak Instruments

We study inference on linear functionals in the nonparametric instrumental variable (NPIV) problem with a discretely-valued instrument under a many-weak-instruments asymptotic regime, where the number of instrument values grows with the sample size. A key motivating example is estimating long-term causal effects in a new experiment with only short-term outcomes, using past experiments to instrument for the effect of short- on long-term outcomes. Here, the assignment to a past experiment serves as the instrument: we have many past experiments but only a limited number of units in each. Since the structural function is nonparametric but constrained by only finitely many moment restrictions, point identification typically fails. To address this, we consider linear functionals of the minimum-norm solution to the moment restrictions, which is always well-defined. As the number of instrument levels grows, these functionals define an approximating sequence to a target functional, replacing point identification with a weaker asymptotic notion suited to discrete instruments. Extending the Jackknife Instrumental Variable Estimator (JIVE) beyond the classical parametric setting, we propose npJIVE, a nonparametric estimator for solutions to linear inverse problems with many weak instruments. We construct automatic debiased machine learning estimators for linear functionals of both the structural function and its minimum-norm projection, and establish their efficiency in the many-weak-instruments regime.

Generalized Venn and Venn-Abers Calibration with Applications in Conformal Prediction

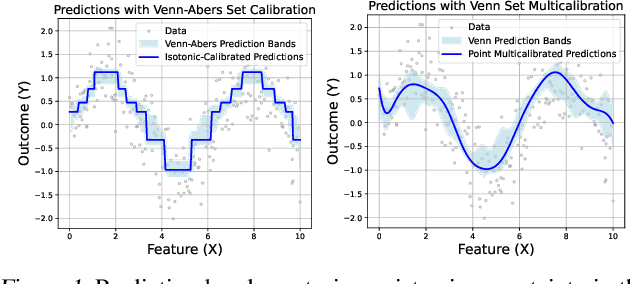
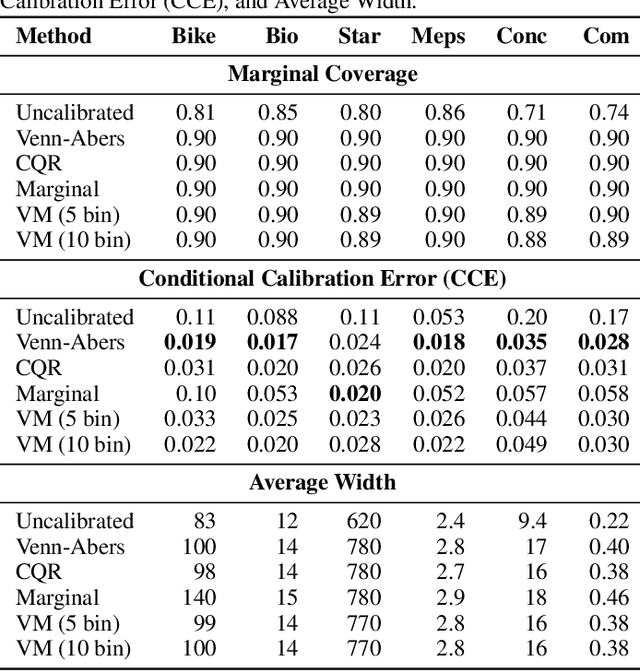
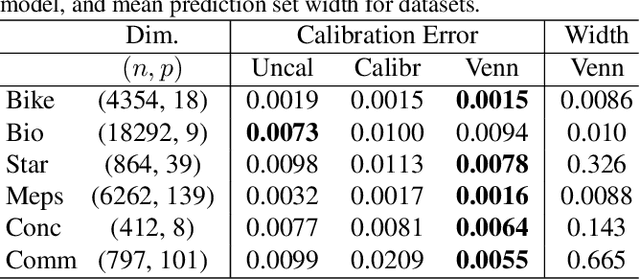
Ensuring model calibration is critical for reliable predictions, yet popular distribution-free methods, such as histogram binning and isotonic regression, provide only asymptotic guarantees. We introduce a unified framework for Venn and Venn-Abers calibration, generalizing Vovk's binary classification approach to arbitrary prediction tasks and loss functions. Venn calibration leverages binning calibrators to construct prediction sets that contain at least one marginally perfectly calibrated point prediction in finite samples, capturing epistemic uncertainty in the calibration process. The width of these sets shrinks asymptotically to zero, converging to a conditionally calibrated point prediction. Furthermore, we propose Venn multicalibration, a novel methodology for finite-sample calibration across subpopulations. For quantile loss, group-conditional and multicalibrated conformal prediction arise as special cases of Venn multicalibration, and Venn calibration produces novel conformal prediction intervals that achieve quantile-conditional coverage. As a separate contribution, we extend distribution-free conditional calibration guarantees of histogram binning and isotonic calibration to general losses.

Automatic Double Reinforcement Learning in Semiparametric Markov Decision Processes with Applications to Long-Term Causal Inference

Double reinforcement learning (DRL) enables statistically efficient inference on the value of a policy in a nonparametric Markov Decision Process (MDP) given trajectories generated by another policy. However, this approach necessarily requires stringent overlap between the state distributions, which is often violated in practice. To relax this requirement and extend DRL, we study efficient inference on linear functionals of the $Q$-function (of which policy value is a special case) in infinite-horizon, time-invariant MDPs under semiparametric restrictions on the $Q$-function. These restrictions can reduce the overlap requirement and lower the efficiency bound, yielding more precise estimates. As an important example, we study the evaluation of long-term value under domain adaptation, given a few short trajectories from the new domain and restrictions on the difference between the domains. This can be used for long-term causal inference. Our method combines flexible estimates of the $Q$-function and the Riesz representer of the functional of interest (e.g., the stationary state density ratio for policy value) and is automatic in that we do not need to know the form of the latter - only the functional we care about. To address potential model misspecification bias, we extend the adaptive debiased machine learning (ADML) framework of \citet{van2023adaptive} to construct nonparametrically valid and superefficient estimators that adapt to the functional form of the $Q$-function. As a special case, we propose a novel adaptive debiased plug-in estimator that uses isotonic-calibrated fitted $Q$-iteration - a new calibration algorithm for MDPs - to circumvent the computational challenges of estimating debiasing nuisances from min-max objectives.

Stabilized Inverse Probability Weighting via Isotonic Calibration

Inverse weighting with an estimated propensity score is widely used by estimation methods in causal inference to adjust for confounding bias. However, directly inverting propensity score estimates can lead to instability, bias, and excessive variability due to large inverse weights, especially when treatment overlap is limited. In this work, we propose a post-hoc calibration algorithm for inverse propensity weights that generates well-calibrated, stabilized weights from user-supplied, cross-fitted propensity score estimates. Our approach employs a variant of isotonic regression with a loss function specifically tailored to the inverse propensity weights. Through theoretical analysis and empirical studies, we demonstrate that isotonic calibration improves the performance of doubly robust estimators of the average treatment effect.

Automatic doubly robust inference for linear functionals via calibrated debiased machine learning

In causal inference, many estimands of interest can be expressed as a linear functional of the outcome regression function; this includes, for example, average causal effects of static, dynamic and stochastic interventions. For learning such estimands, in this work, we propose novel debiased machine learning estimators that are doubly robust asymptotically linear, thus providing not only doubly robust consistency but also facilitating doubly robust inference (e.g., confidence intervals and hypothesis tests). To do so, we first establish a key link between calibration, a machine learning technique typically used in prediction and classification tasks, and the conditions needed to achieve doubly robust asymptotic linearity. We then introduce calibrated debiased machine learning (C-DML), a unified framework for doubly robust inference, and propose a specific C-DML estimator that integrates cross-fitting, isotonic calibration, and debiased machine learning estimation. A C-DML estimator maintains asymptotic linearity when either the outcome regression or the Riesz representer of the linear functional is estimated sufficiently well, allowing the other to be estimated at arbitrarily slow rates or even inconsistently. We propose a simple bootstrap-assisted approach for constructing doubly robust confidence intervals. Our theoretical and empirical results support the use of C-DML to mitigate bias arising from the inconsistent or slow estimation of nuisance functions.

Adaptive-TMLE for the Average Treatment Effect based on Randomized Controlled Trial Augmented with Real-World Data

We consider the problem of estimating the average treatment effect (ATE) when both randomized control trial (RCT) data and real-world data (RWD) are available. We decompose the ATE estimand as the difference between a pooled-ATE estimand that integrates RCT and RWD and a bias estimand that captures the conditional effect of RCT enrollment on the outcome. We introduce an adaptive targeted minimum loss-based estimation (A-TMLE) framework to estimate them. We prove that the A-TMLE estimator is root-n-consistent and asymptotically normal. Moreover, in finite sample, it achieves the super-efficiency one would obtain had one known the oracle model for the conditional effect of the RCT enrollment on the outcome. Consequently, the smaller the working model of the bias induced by the RWD is, the greater our estimator's efficiency, while our estimator will always be at least as efficient as an efficient estimator that uses the RCT data only. A-TMLE outperforms existing methods in simulations by having smaller mean-squared-error and 95% confidence intervals. A-TMLE could help utilize RWD to improve the efficiency of randomized trial results without biasing the estimates of intervention effects. This approach could allow for smaller, faster trials, decreasing the time until patients can receive effective treatments.

Self-Consistent Conformal Prediction

In decision-making guided by machine learning, decision-makers often take identical actions in contexts with identical predicted outcomes. Conformal prediction helps decision-makers quantify outcome uncertainty for actions, allowing for better risk management. Inspired by this perspective, we introduce self-consistent conformal prediction, which yields both Venn-Abers calibrated predictions and conformal prediction intervals that are valid conditional on actions prompted by model predictions. Our procedure can be applied post-hoc to any black-box predictor to provide rigorous, action-specific decision-making guarantees. Numerical experiments show our approach strikes a balance between interval efficiency and conditional validity.

Combining T-learning and DR-learning: a framework for oracle-efficient estimation of causal contrasts

We introduce efficient plug-in (EP) learning, a novel framework for the estimation of heterogeneous causal contrasts, such as the conditional average treatment effect and conditional relative risk. The EP-learning framework enjoys the same oracle-efficiency as Neyman-orthogonal learning strategies, such as DR-learning and R-learning, while addressing some of their primary drawbacks, including that (i) their practical applicability can be hindered by loss function non-convexity; and (ii) they may suffer from poor performance and instability due to inverse probability weighting and pseudo-outcomes that violate bounds. To avoid these drawbacks, EP-learner constructs an efficient plug-in estimator of the population risk function for the causal contrast, thereby inheriting the stability and robustness properties of plug-in estimation strategies like T-learning. Under reasonable conditions, EP-learners based on empirical risk minimization are oracle-efficient, exhibiting asymptotic equivalence to the minimizer of an oracle-efficient one-step debiased estimator of the population risk function. In simulation experiments, we illustrate that EP-learners of the conditional average treatment effect and conditional relative risk outperform state-of-the-art competitors, including T-learner, R-learner, and DR-learner. Open-source implementations of the proposed methods are available in our R package hte3.

Estimating Uncertainty in Multimodal Foundation Models using Public Internet Data

Foundation models are trained on vast amounts of data at scale using self-supervised learning, enabling adaptation to a wide range of downstream tasks. At test time, these models exhibit zero-shot capabilities through which they can classify previously unseen (user-specified) categories. In this paper, we address the problem of quantifying uncertainty in these zero-shot predictions. We propose a heuristic approach for uncertainty estimation in zero-shot settings using conformal prediction with web data. Given a set of classes at test time, we conduct zero-shot classification with CLIP-style models using a prompt template, e.g., "an image of a <category>", and use the same template as a search query to source calibration data from the open web. Given a web-based calibration set, we apply conformal prediction with a novel conformity score that accounts for potential errors in retrieved web data. We evaluate the utility of our proposed method in Biomedical foundation models; our preliminary results show that web-based conformal prediction sets achieve the target coverage with satisfactory efficiency on a variety of biomedical datasets.