Stabilized Inverse Probability Weighting via Isotonic Calibration

Inverse weighting with an estimated propensity score is widely used by estimation methods in causal inference to adjust for confounding bias. However, directly inverting propensity score estimates can lead to instability, bias, and excessive variability due to large inverse weights, especially when treatment overlap is limited. In this work, we propose a post-hoc calibration algorithm for inverse propensity weights that generates well-calibrated, stabilized weights from user-supplied, cross-fitted propensity score estimates. Our approach employs a variant of isotonic regression with a loss function specifically tailored to the inverse propensity weights. Through theoretical analysis and empirical studies, we demonstrate that isotonic calibration improves the performance of doubly robust estimators of the average treatment effect.

Automatic doubly robust inference for linear functionals via calibrated debiased machine learning

In causal inference, many estimands of interest can be expressed as a linear functional of the outcome regression function; this includes, for example, average causal effects of static, dynamic and stochastic interventions. For learning such estimands, in this work, we propose novel debiased machine learning estimators that are doubly robust asymptotically linear, thus providing not only doubly robust consistency but also facilitating doubly robust inference (e.g., confidence intervals and hypothesis tests). To do so, we first establish a key link between calibration, a machine learning technique typically used in prediction and classification tasks, and the conditions needed to achieve doubly robust asymptotic linearity. We then introduce calibrated debiased machine learning (C-DML), a unified framework for doubly robust inference, and propose a specific C-DML estimator that integrates cross-fitting, isotonic calibration, and debiased machine learning estimation. A C-DML estimator maintains asymptotic linearity when either the outcome regression or the Riesz representer of the linear functional is estimated sufficiently well, allowing the other to be estimated at arbitrarily slow rates or even inconsistently. We propose a simple bootstrap-assisted approach for constructing doubly robust confidence intervals. Our theoretical and empirical results support the use of C-DML to mitigate bias arising from the inconsistent or slow estimation of nuisance functions.

Towards a Unified Theory for Semiparametric Data Fusion with Individual-Level Data

We address the goal of conducting inference about a smooth finite-dimensional parameter by utilizing individual-level data from various independent sources. Recent advancements have led to the development of a comprehensive theory capable of handling scenarios where different data sources align with, possibly distinct subsets of, conditional distributions of a single factorization of the joint target distribution. While this theory proves effective in many significant contexts, it falls short in certain common data fusion problems, such as two-sample instrumental variable analysis, settings that integrate data from epidemiological studies with diverse designs (e.g., prospective cohorts and retrospective case-control studies), and studies with variables prone to measurement error that are supplemented by validation studies. In this paper, we extend the aforementioned comprehensive theory to allow for the fusion of individual-level data from sources aligned with conditional distributions that do not correspond to a single factorization of the target distribution. Assuming conditional and marginal distribution alignments, we provide universal results that characterize the class of all influence functions of regular asymptotically linear estimators and the efficient influence function of any pathwise differentiable parameter, irrespective of the number of data sources, the specific parameter of interest, or the statistical model for the target distribution. This theory paves the way for machine-learning debiased, semiparametric efficient estimation.

Combining T-learning and DR-learning: a framework for oracle-efficient estimation of causal contrasts

We introduce efficient plug-in (EP) learning, a novel framework for the estimation of heterogeneous causal contrasts, such as the conditional average treatment effect and conditional relative risk. The EP-learning framework enjoys the same oracle-efficiency as Neyman-orthogonal learning strategies, such as DR-learning and R-learning, while addressing some of their primary drawbacks, including that (i) their practical applicability can be hindered by loss function non-convexity; and (ii) they may suffer from poor performance and instability due to inverse probability weighting and pseudo-outcomes that violate bounds. To avoid these drawbacks, EP-learner constructs an efficient plug-in estimator of the population risk function for the causal contrast, thereby inheriting the stability and robustness properties of plug-in estimation strategies like T-learning. Under reasonable conditions, EP-learners based on empirical risk minimization are oracle-efficient, exhibiting asymptotic equivalence to the minimizer of an oracle-efficient one-step debiased estimator of the population risk function. In simulation experiments, we illustrate that EP-learners of the conditional average treatment effect and conditional relative risk outperform state-of-the-art competitors, including T-learner, R-learner, and DR-learner. Open-source implementations of the proposed methods are available in our R package hte3.

Adaptive debiased machine learning using data-driven model selection techniques

Debiased machine learning estimators for nonparametric inference of smooth functionals of the data-generating distribution can suffer from excessive variability and instability. For this reason, practitioners may resort to simpler models based on parametric or semiparametric assumptions. However, such simplifying assumptions may fail to hold, and estimates may then be biased due to model misspecification. To address this problem, we propose Adaptive Debiased Machine Learning (ADML), a nonparametric framework that combines data-driven model selection and debiased machine learning techniques to construct asymptotically linear, adaptive, and superefficient estimators for pathwise differentiable functionals. By learning model structure directly from data, ADML avoids the bias introduced by model misspecification and remains free from the restrictions of parametric and semiparametric models. While they may exhibit irregular behavior for the target parameter in a nonparametric statistical model, we demonstrate that ADML estimators provides regular and locally uniformly valid inference for a projection-based oracle parameter. Importantly, this oracle parameter agrees with the original target parameter for distributions within an unknown but correctly specified oracle statistical submodel that is learned from the data. This finding implies that there is no penalty, in a local asymptotic sense, for conducting data-driven model selection compared to having prior knowledge of the oracle submodel and oracle parameter. To demonstrate the practical applicability of our theory, we provide a broad class of ADML estimators for estimating the average treatment effect in adaptive partially linear regression models.

Causal isotonic calibration for heterogeneous treatment effects

We propose causal isotonic calibration, a novel nonparametric method for calibrating predictors of heterogeneous treatment effects. In addition, we introduce a novel data-efficient variant of calibration that avoids the need for hold-out calibration sets, which we refer to as cross-calibration. Causal isotonic cross-calibration takes cross-fitted predictors and outputs a single calibrated predictor obtained using all available data. We establish under weak conditions that causal isotonic calibration and cross-calibration both achieve fast doubly-robust calibration rates so long as either the propensity score or outcome regression is estimated well in an appropriate sense. The proposed causal isotonic calibrator can be wrapped around any black-box learning algorithm to provide strong distribution-free calibration guarantees while preserving predictive performance.

A unified approach for inference on algorithm-agnostic variable importance

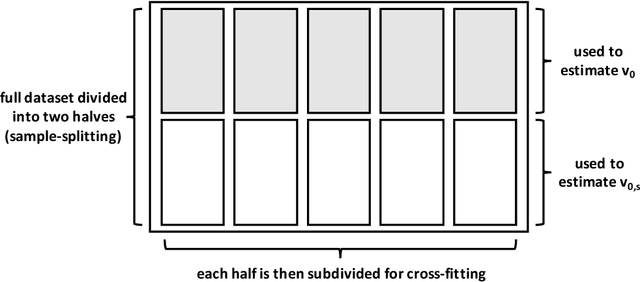
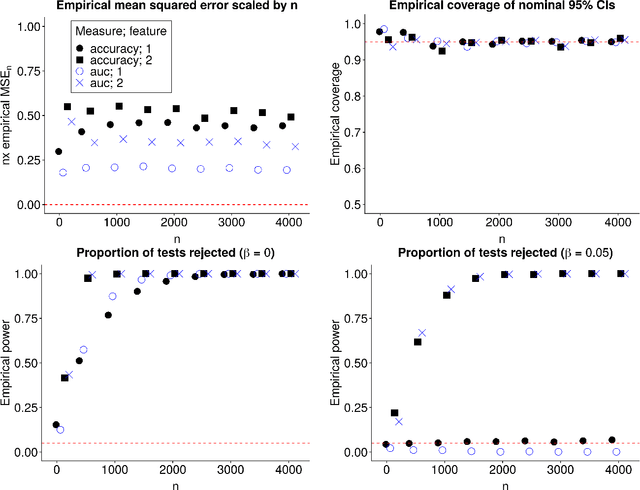
In many applications, it is of interest to assess the relative contribution of features (or subsets of features) toward the goal of predicting a response -- in other words, to gauge the variable importance of features. Most recent work on variable importance assessment has focused on describing the importance of features within the confines of a given prediction algorithm. However, such assessment does not necessarily characterize the prediction potential of features, and may provide a misleading reflection of the intrinsic value of these features. To address this limitation, we propose a general framework for nonparametric inference on interpretable algorithm-agnostic variable importance. We define variable importance as a population-level contrast between the oracle predictiveness of all available features versus all features except those under consideration. We propose a nonparametric efficient estimation procedure that allows the construction of valid confidence intervals, even when machine learning techniques are used. We also outline a valid strategy for testing the null importance hypothesis. Through simulations, we show that our proposal has good operating characteristics, and we illustrate its use with data from a study of an antibody against HIV-1 infection.

An Omnibus Nonparametric Test of Equality in Distribution for Unknown Functions

We present a novel family of nonparametric omnibus tests of the hypothesis that two unknown but estimable functions are equal in distribution when applied to the observed data structure. We developed these tests, which represent a generalization of the maximum mean discrepancy tests described in Gretton et al. [2006], using recent developments from the higher-order pathwise differentiability literature. Despite their complex derivation, the associated test statistics can be expressed rather simply as U-statistics. We study the asymptotic behavior of the proposed tests under the null hypothesis and under both fixed and local alternatives. We provide examples to which our tests can be applied and show that they perform well in a simulation study. As an important special case, our proposed tests can be used to determine whether an unknown function, such as the conditional average treatment effect, is equal to zero almost surely.