Towards a Unified Theory for Semiparametric Data Fusion with Individual-Level Data

We address the goal of conducting inference about a smooth finite-dimensional parameter by utilizing individual-level data from various independent sources. Recent advancements have led to the development of a comprehensive theory capable of handling scenarios where different data sources align with, possibly distinct subsets of, conditional distributions of a single factorization of the joint target distribution. While this theory proves effective in many significant contexts, it falls short in certain common data fusion problems, such as two-sample instrumental variable analysis, settings that integrate data from epidemiological studies with diverse designs (e.g., prospective cohorts and retrospective case-control studies), and studies with variables prone to measurement error that are supplemented by validation studies. In this paper, we extend the aforementioned comprehensive theory to allow for the fusion of individual-level data from sources aligned with conditional distributions that do not correspond to a single factorization of the target distribution. Assuming conditional and marginal distribution alignments, we provide universal results that characterize the class of all influence functions of regular asymptotically linear estimators and the efficient influence function of any pathwise differentiable parameter, irrespective of the number of data sources, the specific parameter of interest, or the statistical model for the target distribution. This theory paves the way for machine-learning debiased, semiparametric efficient estimation.

A note on efficient minimum cost adjustment sets in causal graphical models

We study the selection of adjustment sets for estimating the interventional mean under an individualized treatment rule. We assume a non-parametric causal graphical model with, possibly, hidden variables and at least one adjustment set comprised of observable variables. Moreover, we assume that observable variables have positive costs associated with them. We define the cost of an observable adjustment set as the sum of the costs of the variables that comprise it. We show that in this setting there exist adjustment sets that are minimum cost optimal, in the sense that they yield non-parametric estimators of the interventional mean with the smallest asymptotic variance among those that control for observable adjustment sets that have minimum cost. Our results are based on the construction of a special flow network associated with the original causal graph. We show that a minimum cost optimal adjustment set can be found by computing a maximum flow on the network, and then finding the set of vertices that are reachable from the source by augmenting paths. The optimaladj Python package implements the algorithms introduced in this paper.

Efficient adjustment sets in causal graphical models with hidden variables

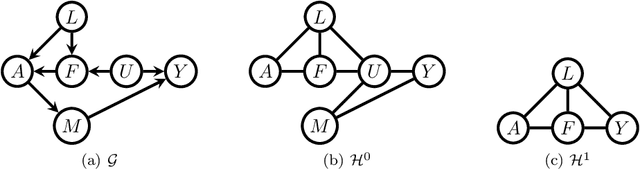
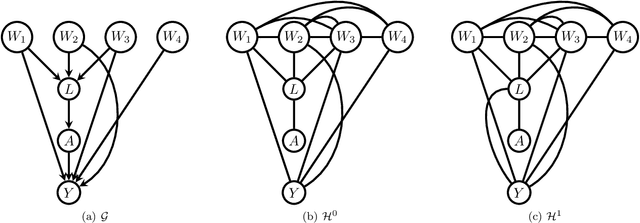
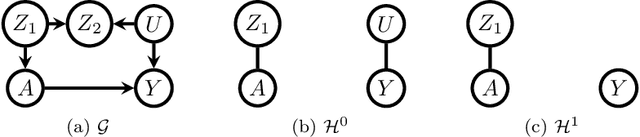
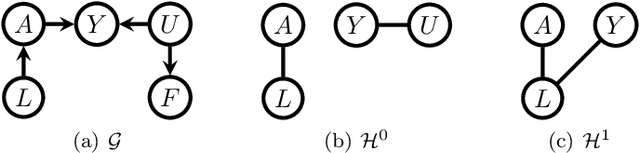
We study the selection of covariate adjustment sets for estimating the value of point exposure dynamic policies, also known as dynamic treatment regimes, assuming a non-parametric causal graphical model with hidden variables, in which at least one adjustment set is fully observable. We show that recently developed criteria, for graphs without hidden variables, to compare the asymptotic variance of non-parametric estimators of static policy values that control for certain adjustment sets, are also valid under dynamic policies and graphs with hidden variables. We show that there exist adjustment sets that are optimal minimal (minimum), in the sense of yielding estimators with the smallest variance among those that control for adjustment sets that are minimal (of minimum cardinality). Moreover, we show that if either no variables are hidden or if all the observable variables are ancestors of either treatment, outcome, or the variables that are used to decide treatment, a globally optimal adjustment set exists. We provide polynomial time algorithms to compute the globally optimal (when it exists), optimal minimal, and optimal minimum adjustment sets. Our results are based on the construction of an undirected graph in which vertex cuts between the treatment and outcome variables correspond to adjustment sets. In this undirected graph, a partial order between minimal vertex cuts can be defined that makes the set of minimal cuts a lattice. This partial order corresponds directly to the ordering of the asymptotic variances of the corresponding non-parametrically adjusted estimators.

Efficient adjustment sets for population average treatment effect estimation in non-parametric causal graphical models

The method of covariate adjustment is often used for estimation of population average treatment effects in observational studies. Graphical rules for determining all valid covariate adjustment sets from an assumed causal graphical model are well known. Restricting attention to causal linear models, a recent article derived two novel graphical criteria: one to compare the asymptotic variance of linear regression treatment effect estimators that control for certain distinct adjustment sets and another to identify the optimal adjustment set that yields the least squares treatment effect estimator with the smallest asymptotic variance among consistent adjusted least squares estimators. In this paper we show that the same graphical criteria can be used in non-parametric causal graphical models when treatment effects are estimated by contrasts involving non-parametrically adjusted estimators of the interventional means. We also provide a graphical criterion for determining the optimal adjustment set among the minimal adjustment sets, which is valid for both linear and non-parametric estimators. We provide a new graphical criterion for comparing time dependent adjustment sets, that is, sets comprised by covariates that adjust for future treatments and that are themselves affected by earlier treatments. We show by example that uniformly optimal time dependent adjustment sets do not always exist. In addition, for point interventions, we provide a sound and complete graphical criterion for determining when a non-parametric optimally adjusted estimator of an interventional mean, or of a contrast of interventional means, is as efficient as an efficient estimator of the same parameter that exploits the information in the conditional independencies encoded in the non-parametric causal graphical model.

A unifying approach for doubly-robust $\ell_1$ regularized estimation of causal contrasts

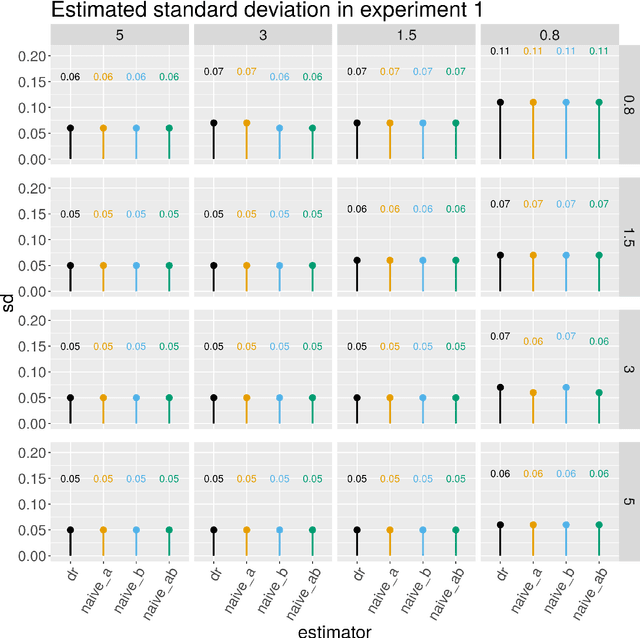
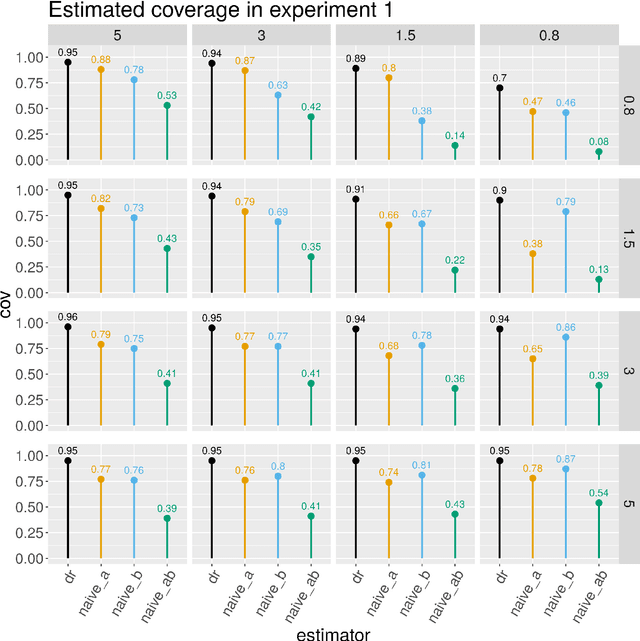
We consider inference about a scalar parameter under a non-parametric model based on a one-step estimator computed as a plug in estimator plus the empirical mean of an estimator of the parameter's influence function. We focus on a class of parameters that have influence function which depends on two infinite dimensional nuisance functions and such that the bias of the one-step estimator of the parameter of interest is the expectation of the product of the estimation errors of the two nuisance functions. Our class includes many important treatment effect contrasts of interest in causal inference and econometrics, such as ATE, ATT, an integrated causal contrast with a continuous treatment, and the mean of an outcome missing not at random. We propose estimators of the target parameter that entertain approximately sparse regression models for the nuisance functions allowing for the number of potential confounders to be even larger than the sample size. By employing sample splitting, cross-fitting and $\ell_1$-regularized regression estimators of the nuisance functions based on objective functions whose directional derivatives agree with those of the parameter's influence function, we obtain estimators of the target parameter with two desirable robustness properties: (1) they are rate doubly-robust in that they are root-n consistent and asymptotically normal when both nuisance functions follow approximately sparse models, even if one function has a very non-sparse regression coefficient, so long as the other has a sufficiently sparse regression coefficient, and (2) they are model doubly-robust in that they are root-n consistent and asymptotically normal even if one of the nuisance functions does not follow an approximately sparse model so long as the other nuisance function follows an approximately sparse model with a sufficiently sparse regression coefficient.