Efficient adjustment sets in causal graphical models with hidden variables

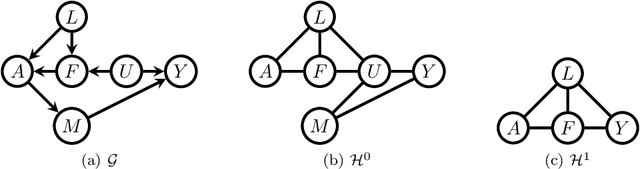
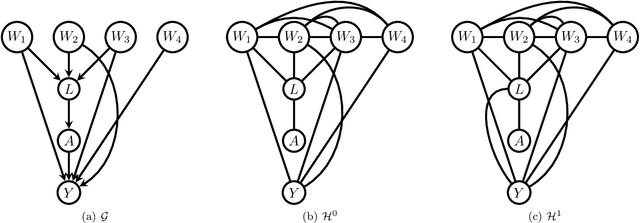
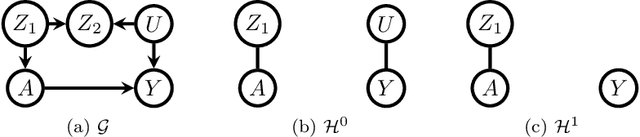
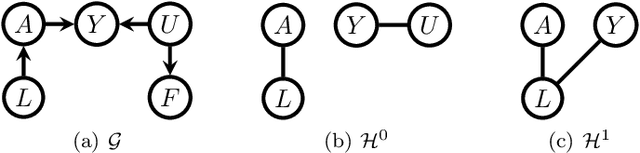
We study the selection of covariate adjustment sets for estimating the value of point exposure dynamic policies, also known as dynamic treatment regimes, assuming a non-parametric causal graphical model with hidden variables, in which at least one adjustment set is fully observable. We show that recently developed criteria, for graphs without hidden variables, to compare the asymptotic variance of non-parametric estimators of static policy values that control for certain adjustment sets, are also valid under dynamic policies and graphs with hidden variables. We show that there exist adjustment sets that are optimal minimal (minimum), in the sense of yielding estimators with the smallest variance among those that control for adjustment sets that are minimal (of minimum cardinality). Moreover, we show that if either no variables are hidden or if all the observable variables are ancestors of either treatment, outcome, or the variables that are used to decide treatment, a globally optimal adjustment set exists. We provide polynomial time algorithms to compute the globally optimal (when it exists), optimal minimal, and optimal minimum adjustment sets. Our results are based on the construction of an undirected graph in which vertex cuts between the treatment and outcome variables correspond to adjustment sets. In this undirected graph, a partial order between minimal vertex cuts can be defined that makes the set of minimal cuts a lattice. This partial order corresponds directly to the ordering of the asymptotic variances of the corresponding non-parametrically adjusted estimators.