Differentiable Programming for Differential Equations: A Review

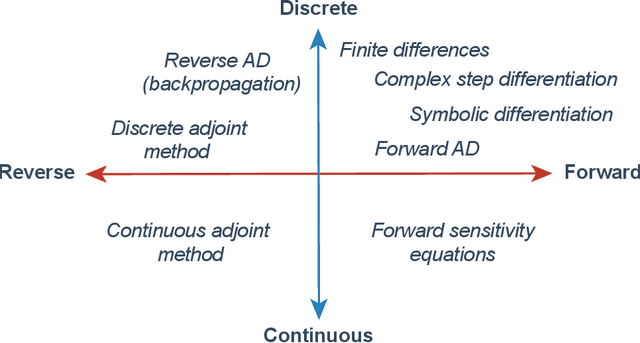
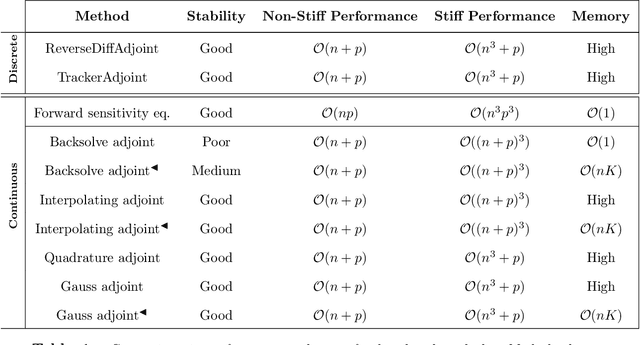
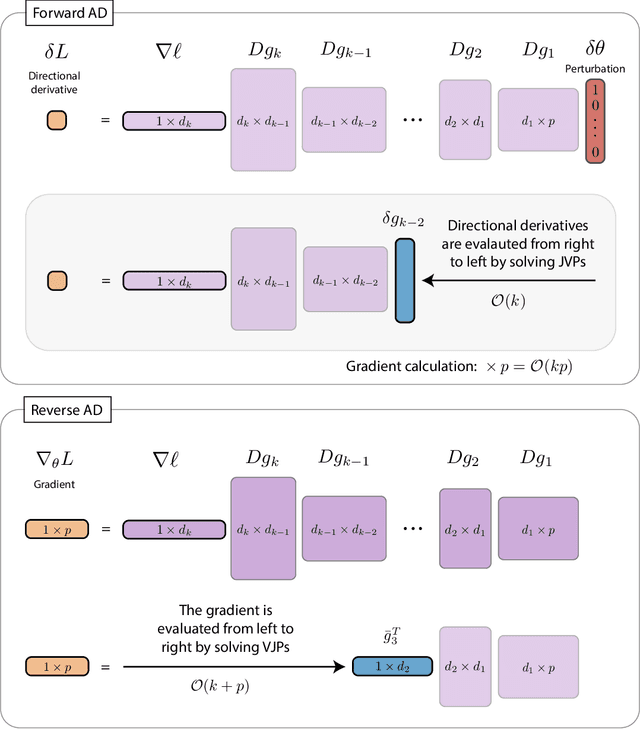
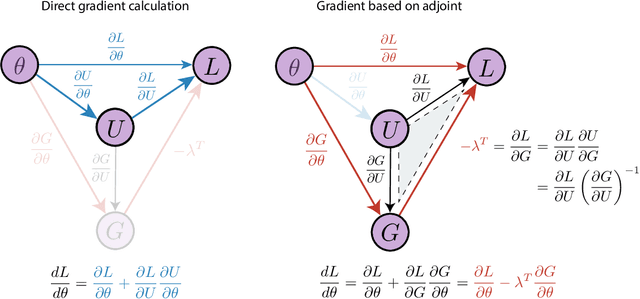
The differentiable programming paradigm is a cornerstone of modern scientific computing. It refers to numerical methods for computing the gradient of a numerical model's output. Many scientific models are based on differential equations, where differentiable programming plays a crucial role in calculating model sensitivities, inverting model parameters, and training hybrid models that combine differential equations with data-driven approaches. Furthermore, recognizing the strong synergies between inverse methods and machine learning offers the opportunity to establish a coherent framework applicable to both fields. Differentiating functions based on the numerical solution of differential equations is non-trivial. Numerous methods based on a wide variety of paradigms have been proposed in the literature, each with pros and cons specific to the type of problem investigated. Here, we provide a comprehensive review of existing techniques to compute derivatives of numerical solutions of differential equations. We first discuss the importance of gradients of solutions of differential equations in a variety of scientific domains. Second, we lay out the mathematical foundations of the various approaches and compare them with each other. Third, we cover the computational considerations and explore the solutions available in modern scientific software. Last but not least, we provide best-practices and recommendations for practitioners. We hope that this work accelerates the fusion of scientific models and data, and fosters a modern approach to scientific modelling.

Choosing the parameter of the Fermat distance: navigating geometry and noise

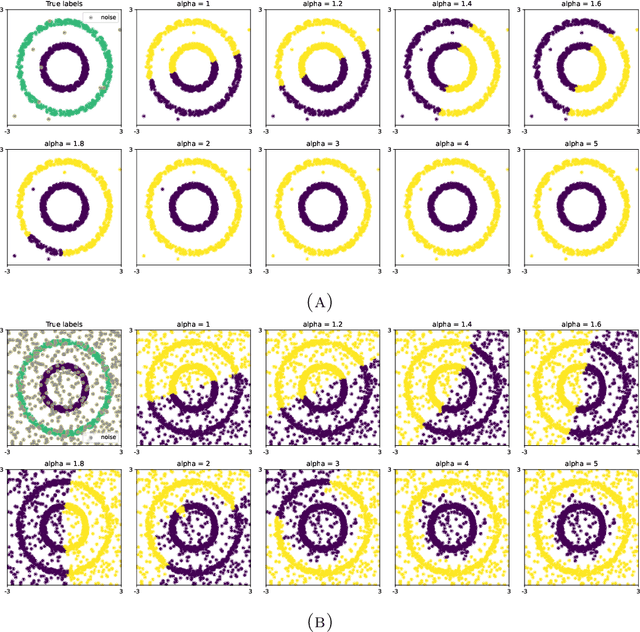
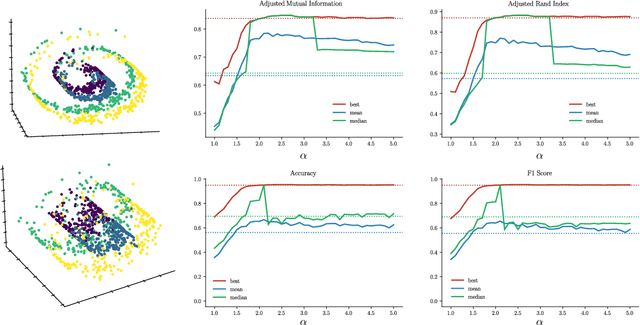
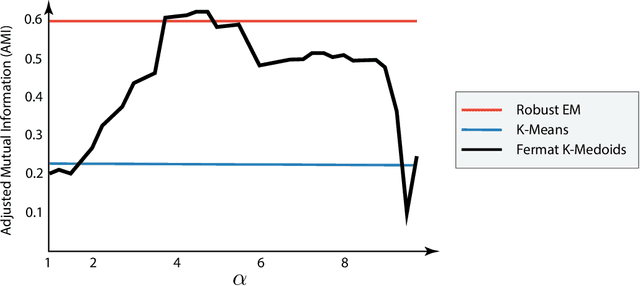
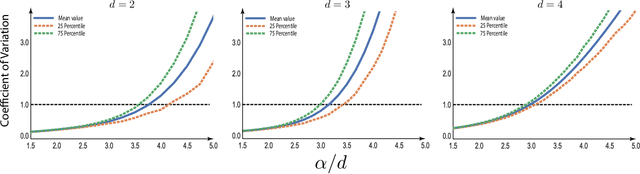
The Fermat distance has been recently established as a useful tool for machine learning tasks when a natural distance is not directly available to the practitioner or to improve the results given by Euclidean distances by exploding the geometrical and statistical properties of the dataset. This distance depends on a parameter $\alpha$ that greatly impacts the performance of subsequent tasks. Ideally, the value of $\alpha$ should be large enough to navigate the geometric intricacies inherent to the problem. At the same, it should remain restrained enough to sidestep any deleterious ramifications stemming from noise during the process of distance estimation. We study both theoretically and through simulations how to select this parameter.

Efficient adjustment sets in causal graphical models with hidden variables

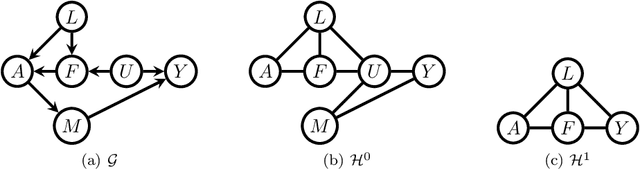
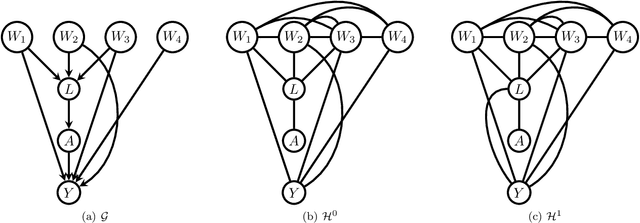
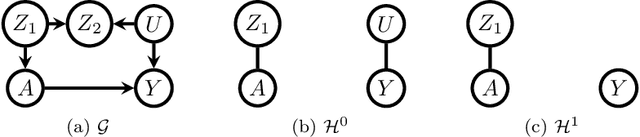
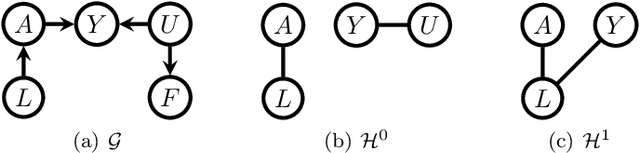
We study the selection of covariate adjustment sets for estimating the value of point exposure dynamic policies, also known as dynamic treatment regimes, assuming a non-parametric causal graphical model with hidden variables, in which at least one adjustment set is fully observable. We show that recently developed criteria, for graphs without hidden variables, to compare the asymptotic variance of non-parametric estimators of static policy values that control for certain adjustment sets, are also valid under dynamic policies and graphs with hidden variables. We show that there exist adjustment sets that are optimal minimal (minimum), in the sense of yielding estimators with the smallest variance among those that control for adjustment sets that are minimal (of minimum cardinality). Moreover, we show that if either no variables are hidden or if all the observable variables are ancestors of either treatment, outcome, or the variables that are used to decide treatment, a globally optimal adjustment set exists. We provide polynomial time algorithms to compute the globally optimal (when it exists), optimal minimal, and optimal minimum adjustment sets. Our results are based on the construction of an undirected graph in which vertex cuts between the treatment and outcome variables correspond to adjustment sets. In this undirected graph, a partial order between minimal vertex cuts can be defined that makes the set of minimal cuts a lattice. This partial order corresponds directly to the ordering of the asymptotic variances of the corresponding non-parametrically adjusted estimators.