Compositional Entailment Learning for Hyperbolic Vision-Language Models

Image-text representation learning forms a cornerstone in vision-language models, where pairs of images and textual descriptions are contrastively aligned in a shared embedding space. Since visual and textual concepts are naturally hierarchical, recent work has shown that hyperbolic space can serve as a high-potential manifold to learn vision-language representation with strong downstream performance. In this work, for the first time we show how to fully leverage the innate hierarchical nature of hyperbolic embeddings by looking beyond individual image-text pairs. We propose Compositional Entailment Learning for hyperbolic vision-language models. The idea is that an image is not only described by a sentence but is itself a composition of multiple object boxes, each with their own textual description. Such information can be obtained freely by extracting nouns from sentences and using openly available localized grounding models. We show how to hierarchically organize images, image boxes, and their textual descriptions through contrastive and entailment-based objectives. Empirical evaluation on a hyperbolic vision-language model trained with millions of image-text pairs shows that the proposed compositional learning approach outperforms conventional Euclidean CLIP learning, as well as recent hyperbolic alternatives, with better zero-shot and retrieval generalization and clearly stronger hierarchical performance.

In-Context Learning Improves Compositional Understanding of Vision-Language Models

Vision-Language Models (VLMs) have shown remarkable capabilities in a large number of downstream tasks. Nonetheless, compositional image understanding remains a rather difficult task due to the object bias present in training data. In this work, we investigate the reasons for such a lack of capability by performing an extensive bench-marking of compositional understanding in VLMs. We compare contrastive models with generative ones and analyze their differences in architecture, pre-training data, and training tasks and losses. Furthermore, we leverage In-Context Learning (ICL) as a way to improve the ability of VLMs to perform more complex reasoning and understanding given an image. Our extensive experiments demonstrate that our proposed approach outperforms baseline models across multiple compositional understanding datasets.

Differentiable Programming for Differential Equations: A Review

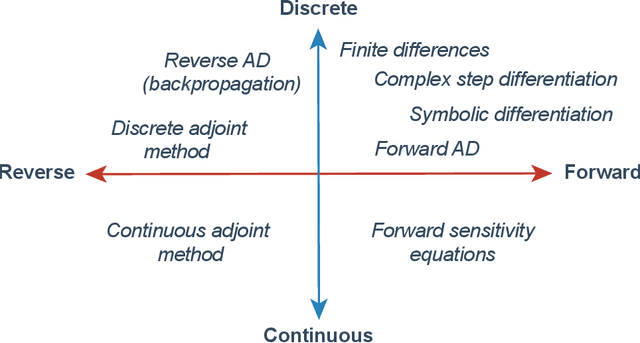
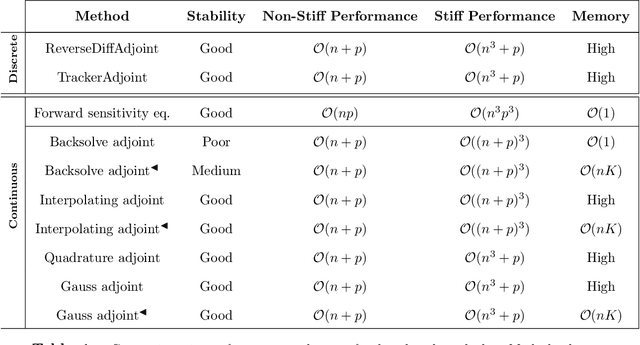
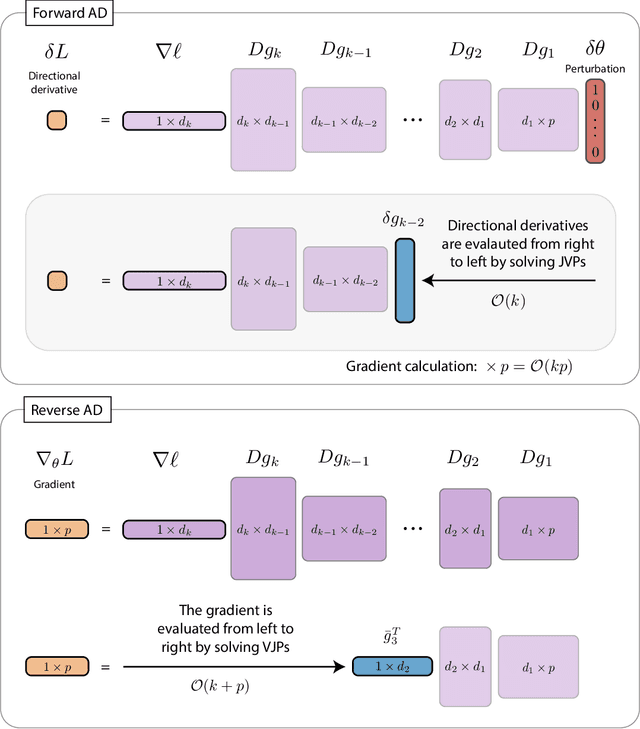
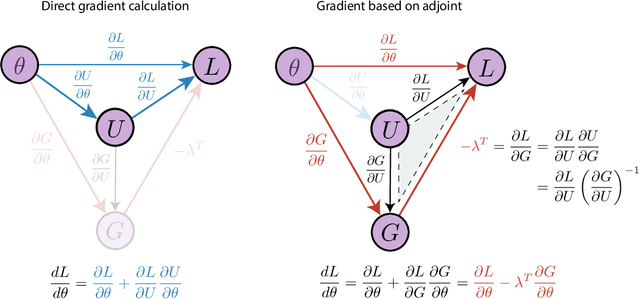
The differentiable programming paradigm is a cornerstone of modern scientific computing. It refers to numerical methods for computing the gradient of a numerical model's output. Many scientific models are based on differential equations, where differentiable programming plays a crucial role in calculating model sensitivities, inverting model parameters, and training hybrid models that combine differential equations with data-driven approaches. Furthermore, recognizing the strong synergies between inverse methods and machine learning offers the opportunity to establish a coherent framework applicable to both fields. Differentiating functions based on the numerical solution of differential equations is non-trivial. Numerous methods based on a wide variety of paradigms have been proposed in the literature, each with pros and cons specific to the type of problem investigated. Here, we provide a comprehensive review of existing techniques to compute derivatives of numerical solutions of differential equations. We first discuss the importance of gradients of solutions of differential equations in a variety of scientific domains. Second, we lay out the mathematical foundations of the various approaches and compare them with each other. Third, we cover the computational considerations and explore the solutions available in modern scientific software. Last but not least, we provide best-practices and recommendations for practitioners. We hope that this work accelerates the fusion of scientific models and data, and fosters a modern approach to scientific modelling.

[RE] Modeling Personalized Item Frequency Information for Next-basket Recommendation

This paper focuses on reproducing and extending the results of the paper: "Modeling Personalized Item Frequency Information for Next-basket Recommendation" which introduced the TIFU-KNN model and proposed to utilize Personalized Item Frequency (PIF) for Next Basket Recommendation (NBR). We utilized publicly available grocery shopping datasets used in the original paper and incorporated additional datasets to assess the generalizability of the findings. We evaluated the performance of the models using metrics such as Recall@K, NDCG@K, personalized-hit ratio (PHR), and Mean Reciprocal Rank (MRR). Furthermore, we conducted a thorough examination of fairness by considering user characteristics such as average basket size, item popularity, and novelty. Lastly, we introduced novel $\beta$-VAE architecture to model NBR. The experimental results confirmed that the reproduced model, TIFU-KNN, outperforms the baseline model, Personal Top Frequency, on various datasets and metrics. The findings also highlight the challenges posed by smaller basket sizes in some datasets and suggest avenues for future research to improve NBR performance.

Hitting "Probe"rty with Non-Linearity, and More

Structural probes learn a linear transformation to find how dependency trees are embedded in the hidden states of language models. This simple design may not allow for full exploitation of the structure of the encoded information. Hence, to investigate the structure of the encoded information to its full extent, we incorporate non-linear structural probes. We reformulate the design of non-linear structural probes introduced by White et al. making its design simpler yet effective. We also design a visualization framework that lets us qualitatively assess how strongly two words in a sentence are connected in the predicted dependency tree. We use this technique to understand which non-linear probe variant is good at encoding syntactical information. Additionally, we also use it to qualitatively investigate the structure of dependency trees that BERT encodes in each of its layers. We find that the radial basis function (RBF) is an effective non-linear probe for the BERT model than the linear probe.

Locally Regularized Neural Differential Equations: Some Black Boxes Were Meant to Remain Closed!

Implicit layer deep learning techniques, like Neural Differential Equations, have become an important modeling framework due to their ability to adapt to new problems automatically. Training a neural differential equation is effectively a search over a space of plausible dynamical systems. However, controlling the computational cost for these models is difficult since it relies on the number of steps the adaptive solver takes. Most prior works have used higher-order methods to reduce prediction timings while greatly increasing training time or reducing both training and prediction timings by relying on specific training algorithms, which are harder to use as a drop-in replacement due to strict requirements on automatic differentiation. In this manuscript, we use internal cost heuristics of adaptive differential equation solvers at stochastic time points to guide the training toward learning a dynamical system that is easier to integrate. We "close the black-box" and allow the use of our method with any adjoint technique for gradient calculations of the differential equation solution. We perform experimental studies to compare our method to global regularization to show that we attain similar performance numbers without compromising the flexibility of implementation on ordinary differential equations (ODEs) and stochastic differential equations (SDEs). We develop two sampling strategies to trade off between performance and training time. Our method reduces the number of function evaluations to 0.556-0.733x and accelerates predictions by 1.3-2x.

Mixing Implicit and Explicit Deep Learning with Skip DEQs and Infinite Time Neural ODEs (Continuous DEQs)

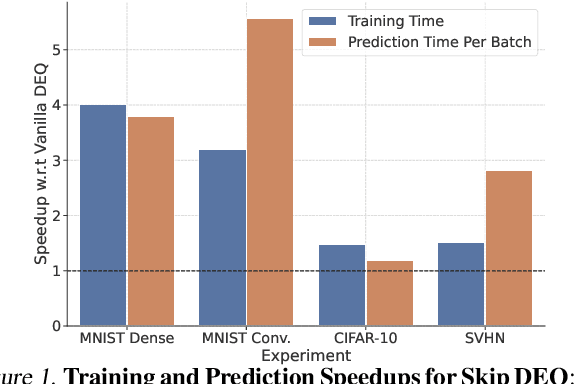
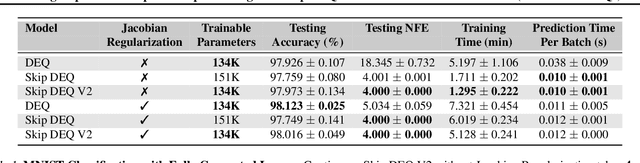
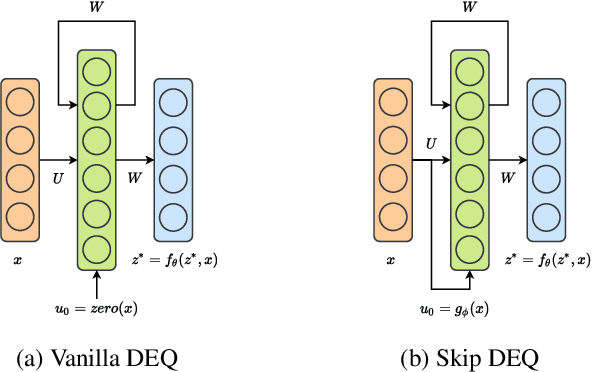
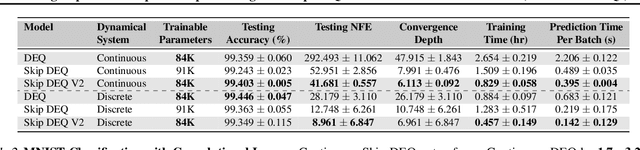
Implicit deep learning architectures, like Neural ODEs and Deep Equilibrium Models (DEQs), separate the definition of a layer from the description of its solution process. While implicit layers allow features such as depth to adapt to new scenarios and inputs automatically, this adaptivity makes its computational expense challenging to predict. Numerous authors have noted that implicit layer techniques can be more computationally intensive than explicit layer methods. In this manuscript, we address the question: is there a way to simultaneously achieve the robustness of implicit layers while allowing the reduced computational expense of an explicit layer? To solve this we develop Skip DEQ, an implicit-explicit (IMEX) layer that simultaneously trains an explicit prediction followed by an implicit correction. We show that training this explicit layer is free and even decreases the training time by 2.5x and prediction time by 3.4x. We then further increase the "implicitness" of the DEQ by redefining the method in terms of an infinite time neural ODE which paradoxically decreases the training cost over a standard neural ODE by not requiring backpropagation through time. We demonstrate how the resulting Continuous Skip DEQ architecture trains more robustly than the original DEQ while achieving faster training and prediction times. Together, this manuscript shows how bridging the dichotomy of implicit and explicit deep learning can combine the advantages of both techniques.

Opening the Blackbox: Accelerating Neural Differential Equations by Regularizing Internal Solver Heuristics

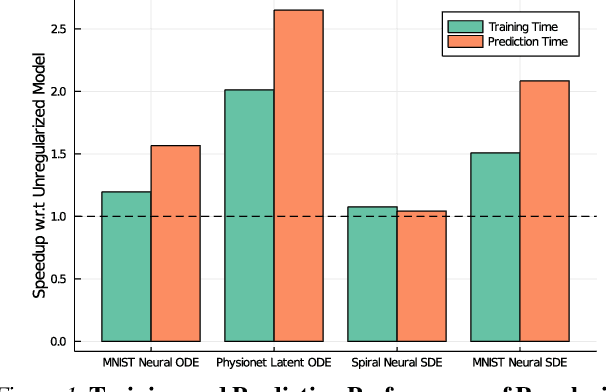
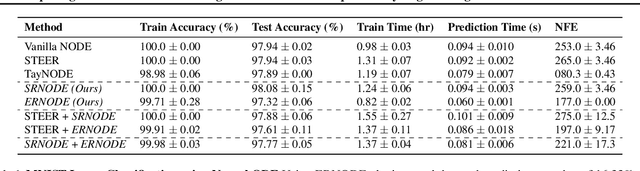
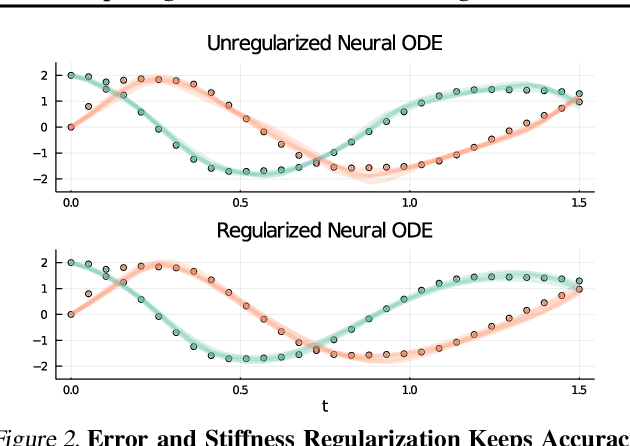
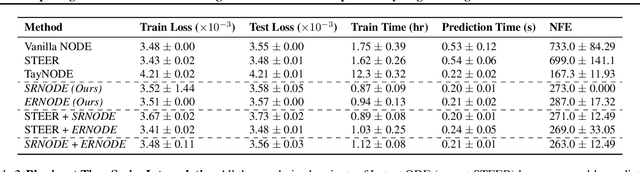
Democratization of machine learning requires architectures that automatically adapt to new problems. Neural Differential Equations (NDEs) have emerged as a popular modeling framework by removing the need for ML practitioners to choose the number of layers in a recurrent model. While we can control the computational cost by choosing the number of layers in standard architectures, in NDEs the number of neural network evaluations for a forward pass can depend on the number of steps of the adaptive ODE solver. But, can we force the NDE to learn the version with the least steps while not increasing the training cost? Current strategies to overcome slow prediction require high order automatic differentiation, leading to significantly higher training time. We describe a novel regularization method that uses the internal cost heuristics of adaptive differential equation solvers combined with discrete adjoint sensitivities to guide the training process towards learning NDEs that are easier to solve. This approach opens up the blackbox numerical analysis behind the differential equation solver's algorithm and directly uses its local error estimates and stiffness heuristics as cheap and accurate cost estimates. We incorporate our method without any change in the underlying NDE framework and show that our method extends beyond Ordinary Differential Equations to accommodate Neural Stochastic Differential Equations. We demonstrate how our approach can halve the prediction time and, unlike other methods which can increase the training time by an order of magnitude, we demonstrate similar reduction in training times. Together this showcases how the knowledge embedded within state-of-the-art equation solvers can be used to enhance machine learning.

Humor@IITK at SemEval-2021 Task 7: Large Language Models for Quantifying Humor and Offensiveness

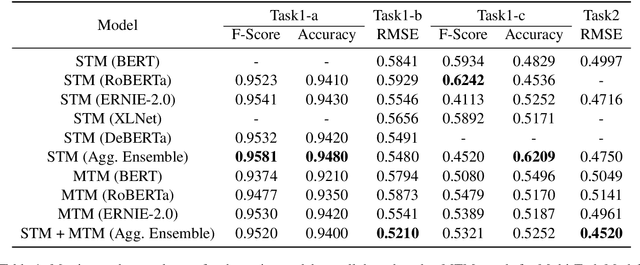
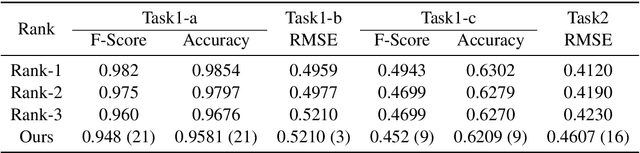
Humor and Offense are highly subjective due to multiple word senses, cultural knowledge, and pragmatic competence. Hence, accurately detecting humorous and offensive texts has several compelling use cases in Recommendation Systems and Personalized Content Moderation. However, due to the lack of an extensive labeled dataset, most prior works in this domain haven't explored large neural models for subjective humor understanding. This paper explores whether large neural models and their ensembles can capture the intricacies associated with humor/offense detection and rating. Our experiments on the SemEval-2021 Task 7: HaHackathon show that we can develop reasonable humor and offense detection systems with such models. Our models are ranked third in subtask 1b and consistently ranked around the top 33% of the leaderboard for the remaining subtasks.

Emergent Road Rules In Multi-Agent Driving Environments

For autonomous vehicles to safely share the road with human drivers, autonomous vehicles must abide by specific "road rules" that human drivers have agreed to follow. "Road rules" include rules that drivers are required to follow by law -- such as the requirement that vehicles stop at red lights -- as well as more subtle social rules -- such as the implicit designation of fast lanes on the highway. In this paper, we provide empirical evidence that suggests that -- instead of hard-coding road rules into self-driving algorithms -- a scalable alternative may be to design multi-agent environments in which road rules emerge as optimal solutions to the problem of maximizing traffic flow. We analyze what ingredients in driving environments cause the emergence of these road rules and find that two crucial factors are noisy perception and agents' spatial density. We provide qualitative and quantitative evidence of the emergence of seven social driving behaviors, ranging from obeying traffic signals to following lanes, all of which emerge from training agents to drive quickly to destinations without colliding. Our results add empirical support for the social road rules that countries worldwide have agreed on for safe, efficient driving.