Temporal horizons in forecasting: a performance-learnability trade-off

When training autoregressive models for dynamical systems, a critical question arises: how far into the future should the model be trained to predict? Too short a horizon may miss long-term trends, while too long a horizon can impede convergence due to accumulating prediction errors. In this work, we formalize this trade-off by analyzing how the geometry of the loss landscape depends on the training horizon. We prove that for chaotic systems, the loss landscape's roughness grows exponentially with the training horizon, while for limit cycles, it grows linearly, making long-horizon training inherently challenging. However, we also show that models trained on long horizons generalize well to short-term forecasts, whereas those trained on short horizons suffer exponentially (resp. linearly) worse long-term predictions in chaotic (resp. periodic) systems. We validate our theory through numerical experiments and discuss practical implications for selecting training horizons. Our results provide a principled foundation for hyperparameter optimization in autoregressive forecasting models.

Differentiable Programming for Differential Equations: A Review

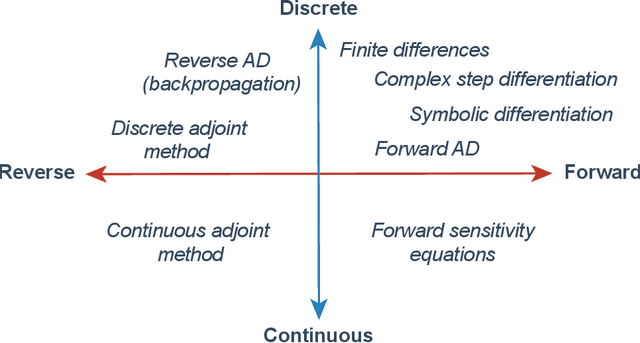
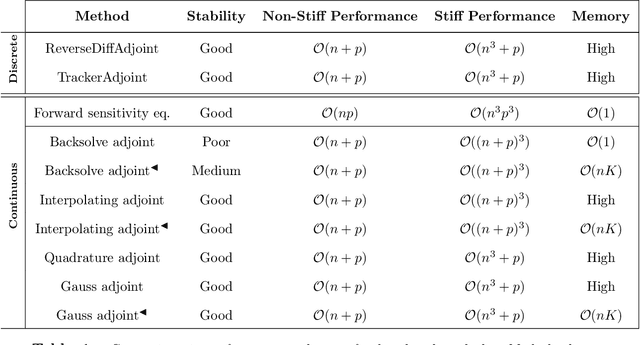
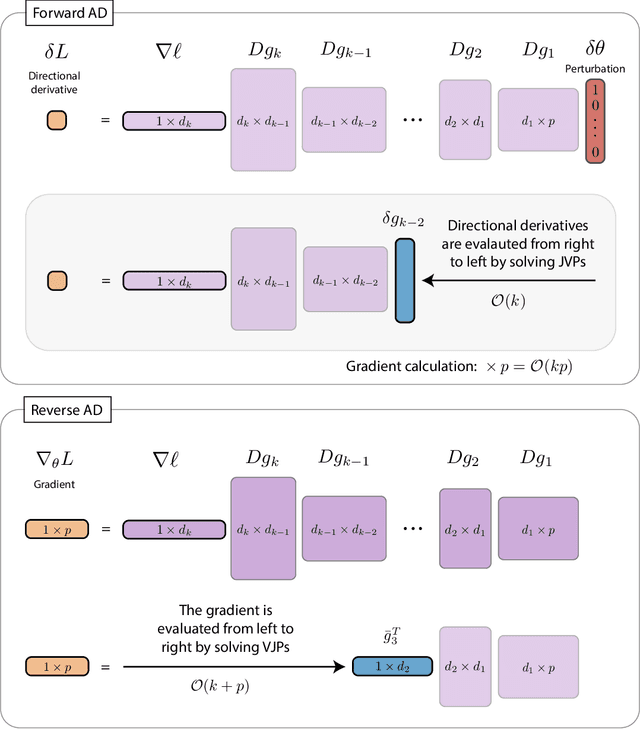
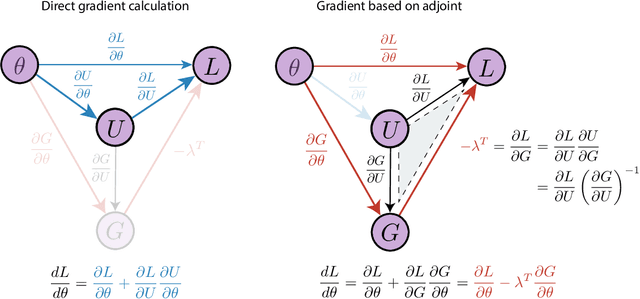
The differentiable programming paradigm is a cornerstone of modern scientific computing. It refers to numerical methods for computing the gradient of a numerical model's output. Many scientific models are based on differential equations, where differentiable programming plays a crucial role in calculating model sensitivities, inverting model parameters, and training hybrid models that combine differential equations with data-driven approaches. Furthermore, recognizing the strong synergies between inverse methods and machine learning offers the opportunity to establish a coherent framework applicable to both fields. Differentiating functions based on the numerical solution of differential equations is non-trivial. Numerous methods based on a wide variety of paradigms have been proposed in the literature, each with pros and cons specific to the type of problem investigated. Here, we provide a comprehensive review of existing techniques to compute derivatives of numerical solutions of differential equations. We first discuss the importance of gradients of solutions of differential equations in a variety of scientific domains. Second, we lay out the mathematical foundations of the various approaches and compare them with each other. Third, we cover the computational considerations and explore the solutions available in modern scientific software. Last but not least, we provide best-practices and recommendations for practitioners. We hope that this work accelerates the fusion of scientific models and data, and fosters a modern approach to scientific modelling.

Deep learning approximations for non-local nonlinear PDEs with Neumann boundary conditions

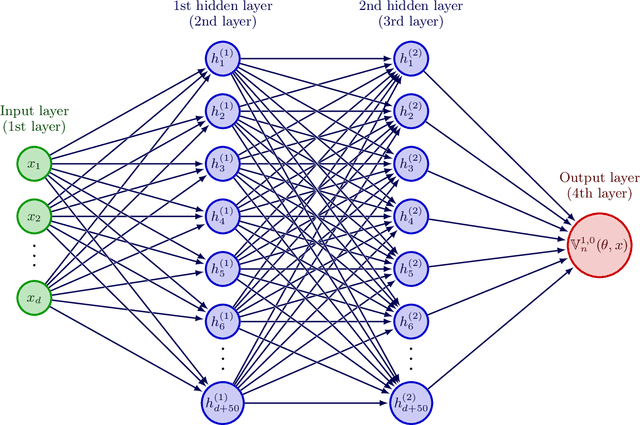
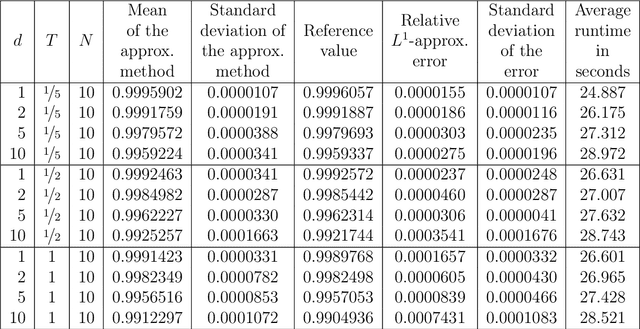
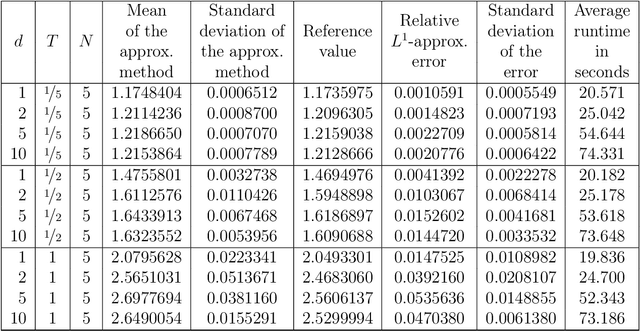
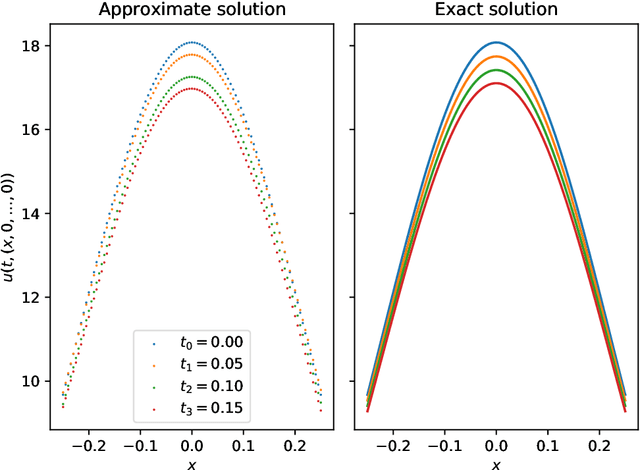
Nonlinear partial differential equations (PDEs) are used to model dynamical processes in a large number of scientific fields, ranging from finance to biology. In many applications standard local models are not sufficient to accurately account for certain non-local phenomena such as, e.g., interactions at a distance. In order to properly capture these phenomena non-local nonlinear PDE models are frequently employed in the literature. In this article we propose two numerical methods based on machine learning and on Picard iterations, respectively, to approximately solve non-local nonlinear PDEs. The proposed machine learning-based method is an extended variant of a deep learning-based splitting-up type approximation method previously introduced in the literature and utilizes neural networks to provide approximate solutions on a subset of the spatial domain of the solution. The Picard iterations-based method is an extended variant of the so-called full history recursive multilevel Picard approximation scheme previously introduced in the literature and provides an approximate solution for a single point of the domain. Both methods are mesh-free and allow non-local nonlinear PDEs with Neumann boundary conditions to be solved in high dimensions. In the two methods, the numerical difficulties arising due to the dimensionality of the PDEs are avoided by (i) using the correspondence between the expected trajectory of reflected stochastic processes and the solution of PDEs (given by the Feynman-Kac formula) and by (ii) using a plain vanilla Monte Carlo integration to handle the non-local term. We evaluate the performance of the two methods on five different PDEs arising in physics and biology. In all cases, the methods yield good results in up to 10 dimensions with short run times. Our work extends recently developed methods to overcome the curse of dimensionality in solving PDEs.