Machine learning the Ising transition: A comparison between discriminative and generative approaches

The detection of phase transitions is a central task in many-body physics. To automate this process, the task can be phrased as a classification problem. Classification problems can be approached in two fundamentally distinct ways: through either a discriminative or a generative method. In general, it is unclear which of these two approaches is most suitable for a given problem. The choice is expected to depend on factors such as the availability of system knowledge, dataset size, desired accuracy, computational resources, and other considerations. In this work, we answer the question of how one should approach the solution of phase-classification problems by performing a numerical case study on the thermal phase transition in the classical two-dimensional square-lattice ferromagnetic Ising model.

Differentiable Programming for Differential Equations: A Review

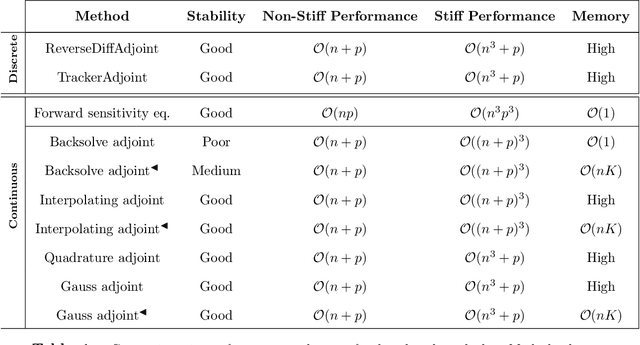
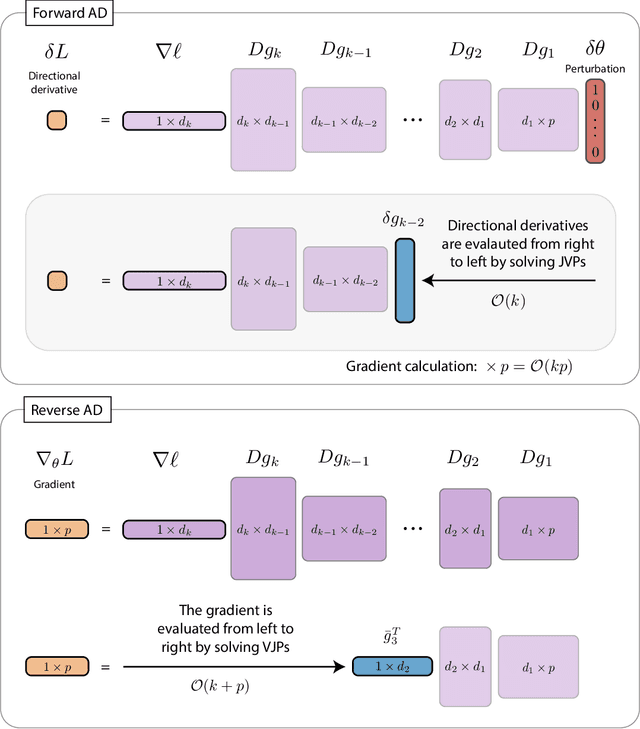
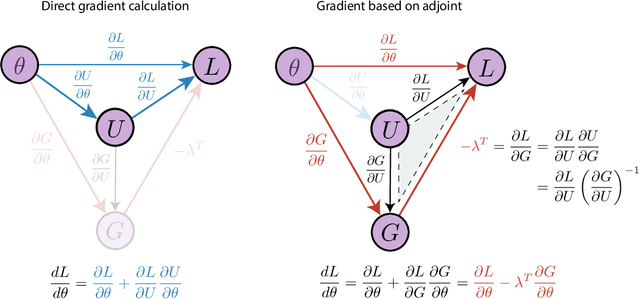
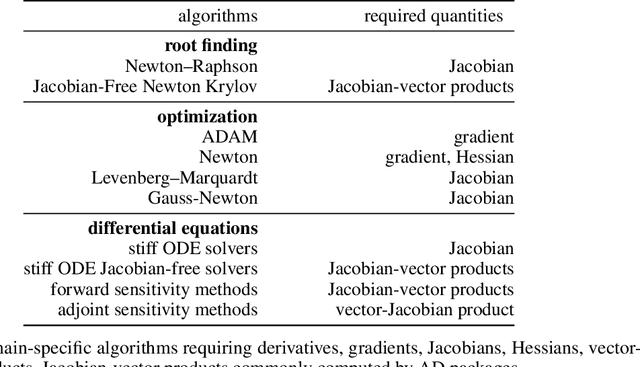
The differentiable programming paradigm is a cornerstone of modern scientific computing. It refers to numerical methods for computing the gradient of a numerical model's output. Many scientific models are based on differential equations, where differentiable programming plays a crucial role in calculating model sensitivities, inverting model parameters, and training hybrid models that combine differential equations with data-driven approaches. Furthermore, recognizing the strong synergies between inverse methods and machine learning offers the opportunity to establish a coherent framework applicable to both fields. Differentiating functions based on the numerical solution of differential equations is non-trivial. Numerous methods based on a wide variety of paradigms have been proposed in the literature, each with pros and cons specific to the type of problem investigated. Here, we provide a comprehensive review of existing techniques to compute derivatives of numerical solutions of differential equations. We first discuss the importance of gradients of solutions of differential equations in a variety of scientific domains. Second, we lay out the mathematical foundations of the various approaches and compare them with each other. Third, we cover the computational considerations and explore the solutions available in modern scientific software. Last but not least, we provide best-practices and recommendations for practitioners. We hope that this work accelerates the fusion of scientific models and data, and fosters a modern approach to scientific modelling.

Phase Transitions in the Output Distribution of Large Language Models

In a physical system, changing parameters such as temperature can induce a phase transition: an abrupt change from one state of matter to another. Analogous phenomena have recently been observed in large language models. Typically, the task of identifying phase transitions requires human analysis and some prior understanding of the system to narrow down which low-dimensional properties to monitor and analyze. Statistical methods for the automated detection of phase transitions from data have recently been proposed within the physics community. These methods are largely system agnostic and, as shown here, can be adapted to study the behavior of large language models. In particular, we quantify distributional changes in the generated output via statistical distances, which can be efficiently estimated with access to the probability distribution over next-tokens. This versatile approach is capable of discovering new phases of behavior and unexplored transitions -- an ability that is particularly exciting in light of the rapid development of language models and their emergent capabilities.

Machine learning phase transitions: Connections to the Fisher information

Despite the widespread use and success of machine-learning techniques for detecting phase transitions from data, their working principle and fundamental limits remain elusive. Here, we explain the inner workings and identify potential failure modes of these techniques by rooting popular machine-learning indicators of phase transitions in information-theoretic concepts. Using tools from information geometry, we prove that several machine-learning indicators of phase transitions approximate the square root of the system's (quantum) Fisher information from below -- a quantity that is known to indicate phase transitions but is often difficult to compute from data. We numerically demonstrate the quality of these bounds for phase transitions in classical and quantum systems.

Fast Detection of Phase Transitions with Multi-Task Learning-by-Confusion

Machine learning has been successfully used to study phase transitions. One of the most popular approaches to identifying critical points from data without prior knowledge of the underlying phases is the learning-by-confusion scheme. As input, it requires system samples drawn from a grid of the parameter whose change is associated with potential phase transitions. Up to now, the scheme required training a distinct binary classifier for each possible splitting of the grid into two sides, resulting in a computational cost that scales linearly with the number of grid points. In this work, we propose and showcase an alternative implementation that only requires the training of a single multi-class classifier. Ideally, such multi-task learning eliminates the scaling with respect to the number of grid points. In applications to the Ising model and an image dataset generated with Stable Diffusion, we find significant speedups that closely correspond to the ideal case, with only minor deviations.

Differentiating Metropolis-Hastings to Optimize Intractable Densities

We develop an algorithm for automatic differentiation of Metropolis-Hastings samplers, allowing us to differentiate through probabilistic inference, even if the model has discrete components within it. Our approach fuses recent advances in stochastic automatic differentiation with traditional Markov chain coupling schemes, providing an unbiased and low-variance gradient estimator. This allows us to apply gradient-based optimization to objectives expressed as expectations over intractable target densities. We demonstrate our approach by finding an ambiguous observation in a Gaussian mixture model and by maximizing the specific heat in an Ising model.

Automatic Differentiation of Programs with Discrete Randomness

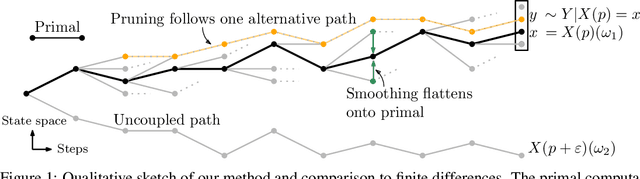
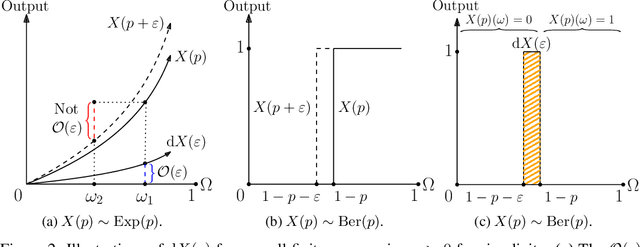
Automatic differentiation (AD), a technique for constructing new programs which compute the derivative of an original program, has become ubiquitous throughout scientific computing and deep learning due to the improved performance afforded by gradient-based optimization. However, AD systems have been restricted to the subset of programs that have a continuous dependence on parameters. Programs that have discrete stochastic behaviors governed by distribution parameters, such as flipping a coin with probability $p$ of being heads, pose a challenge to these systems because the connection between the result (heads vs tails) and the parameters ($p$) is fundamentally discrete. In this paper we develop a new reparameterization-based methodology that allows for generating programs whose expectation is the derivative of the expectation of the original program. We showcase how this method gives an unbiased and low-variance estimator which is as automated as traditional AD mechanisms. We demonstrate unbiased forward-mode AD of discrete-time Markov chains, agent-based models such as Conway's Game of Life, and unbiased reverse-mode AD of a particle filter. Our code is available at https://github.com/gaurav-arya/StochasticAD.jl.

AbstractDifferentiation.jl: Backend-Agnostic Differentiable Programming in Julia

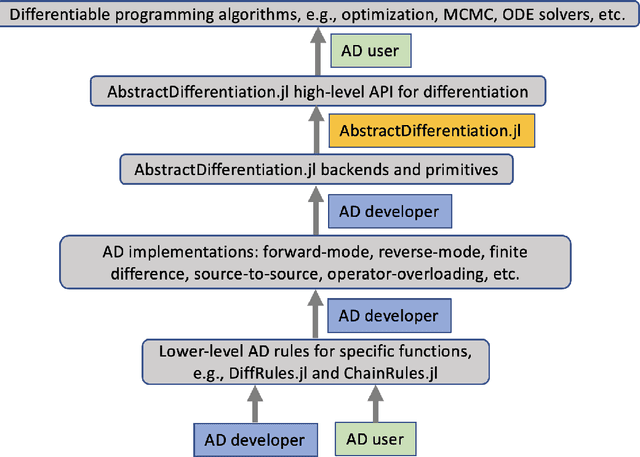
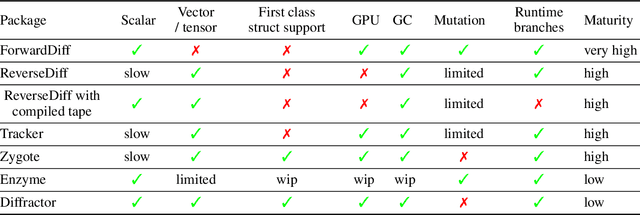
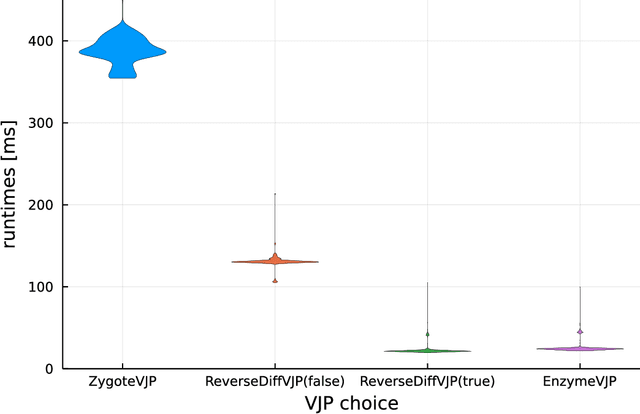
No single Automatic Differentiation (AD) system is the optimal choice for all problems. This means informed selection of an AD system and combinations can be a problem-specific variable that can greatly impact performance. In the Julia programming language, the major AD systems target the same input and thus in theory can compose. Hitherto, switching between AD packages in the Julia Language required end-users to familiarize themselves with the user-facing API of the respective packages. Furthermore, implementing a new, usable AD package required AD package developers to write boilerplate code to define convenience API functions for end-users. As a response to these issues, we present AbstractDifferentiation.jl for the automatized generation of an extensive, unified, user-facing API for any AD package. By splitting the complexity between AD users and AD developers, AD package developers only need to implement one or two primitive definitions to support various utilities for AD users like Jacobians, Hessians and lazy product operators from native primitives such as pullbacks or pushforwards, thus removing tedious -- but so far inevitable -- boilerplate code, and enabling the easy switching and composing between AD implementations for end-users.

Control of Stochastic Quantum Dynamics with Differentiable Programming

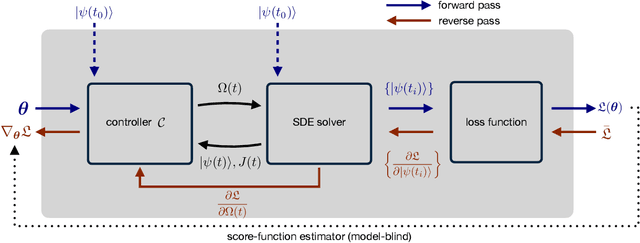
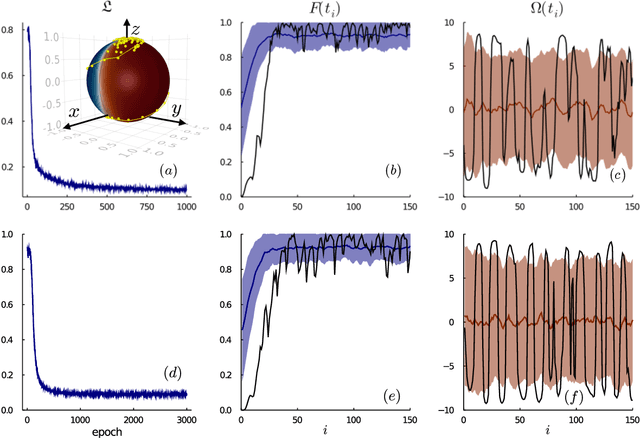
Controlling stochastic dynamics of a quantum system is an indispensable task in fields such as quantum information processing and metrology. Yet, there is no general ready-made approach to design efficient control strategies. Here, we propose a framework for the automated design of control schemes based on differentiable programming ($\partial \mathrm{P}$). We apply this approach to state preparation and stabilization of a qubit subjected to homodyne detection. To this end, we formulate the control task as an optimization problem where the loss function quantifies the distance from the target state and we employ neural networks (NNs) as controllers. The system's time evolution is governed by a stochastic differential equation (SDE). To implement efficient training, we backpropagate the gradient information from the loss function through the SDE solver using adjoint sensitivity methods. As a first example, we feed the quantum state to the controller and focus on different methods to obtain gradients. As a second example, we directly feed the homodyne detection signal to the controller. The instantaneous value of the homodyne current contains only very limited information on the actual state of the system, covered in unavoidable photon-number fluctuations. Despite the resulting poor signal-to-noise ratio, we can train our controller to prepare and stabilize the qubit to a target state with a mean fidelity around 85%. We also compare the solutions found by the NN to a hand-crafted control strategy.