Machine learning the Ising transition: A comparison between discriminative and generative approaches

The detection of phase transitions is a central task in many-body physics. To automate this process, the task can be phrased as a classification problem. Classification problems can be approached in two fundamentally distinct ways: through either a discriminative or a generative method. In general, it is unclear which of these two approaches is most suitable for a given problem. The choice is expected to depend on factors such as the availability of system knowledge, dataset size, desired accuracy, computational resources, and other considerations. In this work, we answer the question of how one should approach the solution of phase-classification problems by performing a numerical case study on the thermal phase transition in the classical two-dimensional square-lattice ferromagnetic Ising model.

Phase Transitions in the Output Distribution of Large Language Models

In a physical system, changing parameters such as temperature can induce a phase transition: an abrupt change from one state of matter to another. Analogous phenomena have recently been observed in large language models. Typically, the task of identifying phase transitions requires human analysis and some prior understanding of the system to narrow down which low-dimensional properties to monitor and analyze. Statistical methods for the automated detection of phase transitions from data have recently been proposed within the physics community. These methods are largely system agnostic and, as shown here, can be adapted to study the behavior of large language models. In particular, we quantify distributional changes in the generated output via statistical distances, which can be efficiently estimated with access to the probability distribution over next-tokens. This versatile approach is capable of discovering new phases of behavior and unexplored transitions -- an ability that is particularly exciting in light of the rapid development of language models and their emergent capabilities.

Machine learning phase transitions: Connections to the Fisher information

Despite the widespread use and success of machine-learning techniques for detecting phase transitions from data, their working principle and fundamental limits remain elusive. Here, we explain the inner workings and identify potential failure modes of these techniques by rooting popular machine-learning indicators of phase transitions in information-theoretic concepts. Using tools from information geometry, we prove that several machine-learning indicators of phase transitions approximate the square root of the system's (quantum) Fisher information from below -- a quantity that is known to indicate phase transitions but is often difficult to compute from data. We numerically demonstrate the quality of these bounds for phase transitions in classical and quantum systems.

Fast Detection of Phase Transitions with Multi-Task Learning-by-Confusion

Machine learning has been successfully used to study phase transitions. One of the most popular approaches to identifying critical points from data without prior knowledge of the underlying phases is the learning-by-confusion scheme. As input, it requires system samples drawn from a grid of the parameter whose change is associated with potential phase transitions. Up to now, the scheme required training a distinct binary classifier for each possible splitting of the grid into two sides, resulting in a computational cost that scales linearly with the number of grid points. In this work, we propose and showcase an alternative implementation that only requires the training of a single multi-class classifier. Ideally, such multi-task learning eliminates the scaling with respect to the number of grid points. In applications to the Ising model and an image dataset generated with Stable Diffusion, we find significant speedups that closely correspond to the ideal case, with only minor deviations.

Machine Learning Product State Distributions from Initial Reactant States for a Reactive Atom-Diatom Collision System

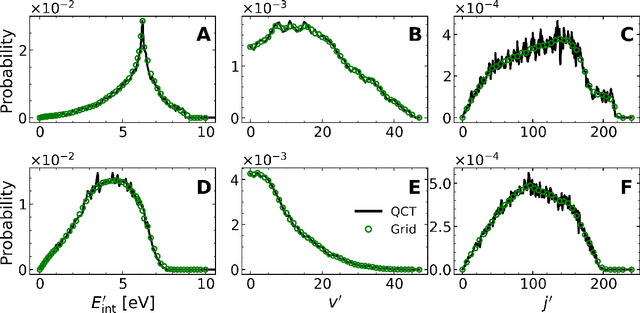
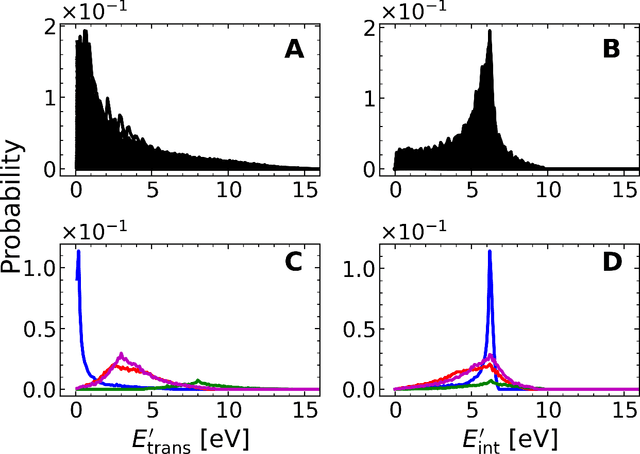
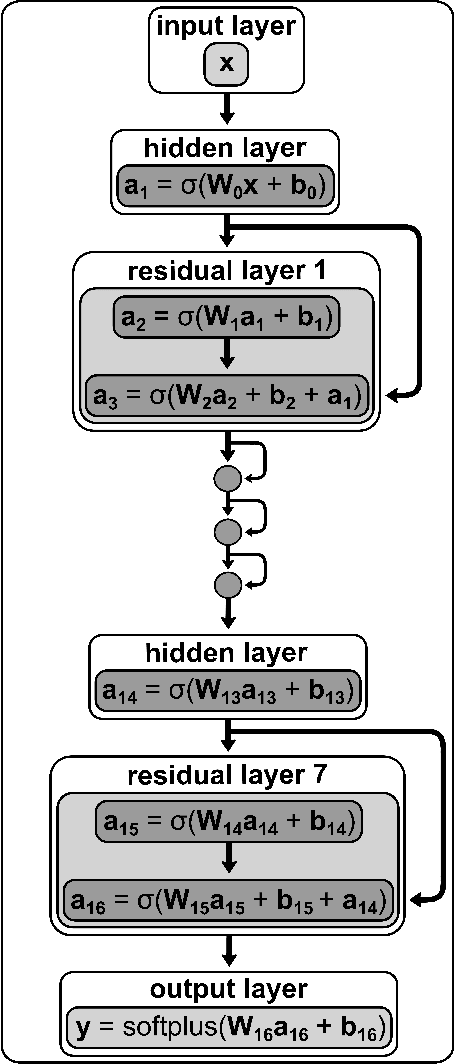
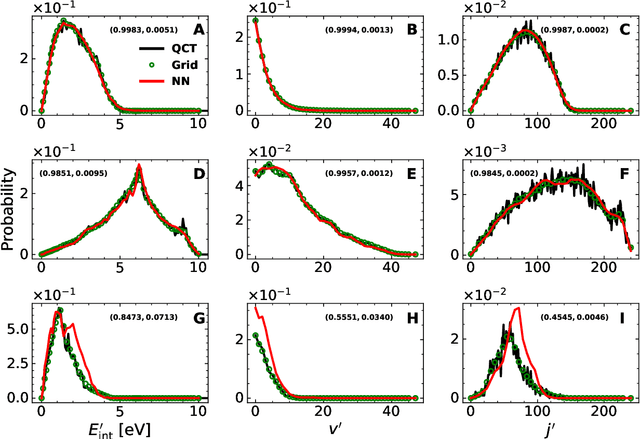
A machine learned (ML) model for predicting product state distributions from specific initial states (state-to-distribution or STD) for reactive atom-diatom collisions is presented and quantitatively tested for the N($^4$S)+O$_{2}$(X$^3 \Sigma_{\rm g}^{-}$) $\rightarrow$ NO(X$^2\Pi$) +O($^3$P) reaction. The reference data set for training the neural network (NN) consists of final state distributions determined from explicit quasi-classical trajectory (QCT) simulations for $\sim 2000$ initial conditions. Overall, the prediction accuracy as quantified by the root-mean-squared difference $(\sim 0.003)$ and the $R^2$ $(\sim 0.99)$ between the reference QCT and predictions of the STD model is high for the test set and off-grid state specific initial conditions and for initial conditions drawn from reactant state distributions characterized by translational, rotational and vibrational temperatures. Compared with a more coarse grained distribution-to-distribution (DTD) model evaluated on the same initial state distributions, the STD model shows comparable performance with the additional benefit of the state resolution in the reactant preparation. Starting from specific initial states also leads to a more diverse range of final state distributions which requires a more expressive neural network to be used compared with DTD. Direct comparison between explicit QCT simulations, the STD model, and the widely used Larsen-Borgnakke (LB) model shows that the STD model is quantitative whereas the LB model is qualitative at best for rotational distributions $P(j')$ and fails for vibrational distributions $P(v')$. As such the STD model can be well-suited for simulating nonequilibrium high-speed flows, e.g., using the direct simulation Monte Carlo method.