Machine Learning Product State Distributions from Initial Reactant States for a Reactive Atom-Diatom Collision System
Paper and Code
Nov 05, 2021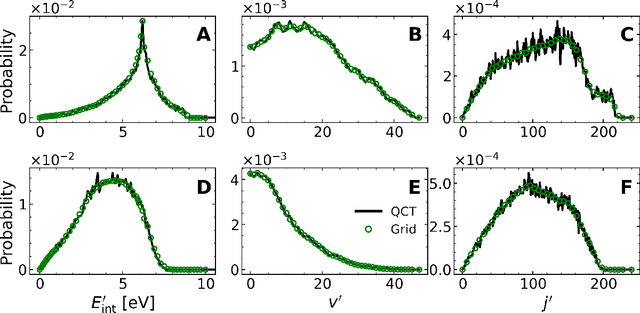
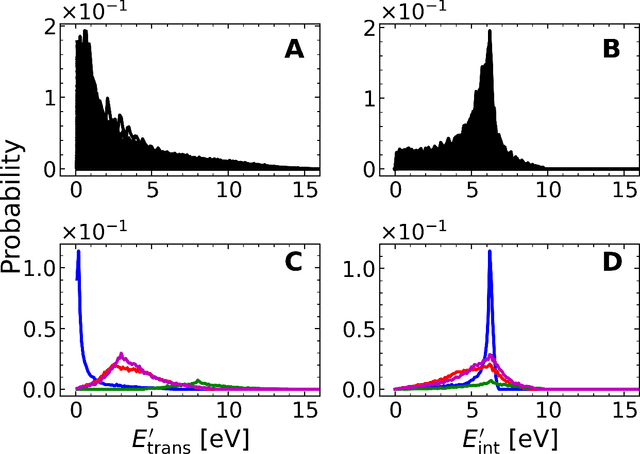
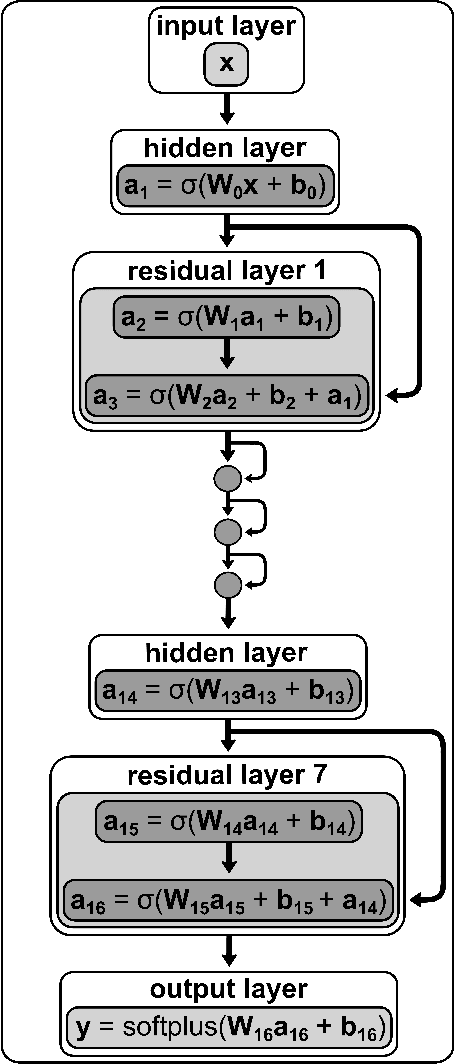
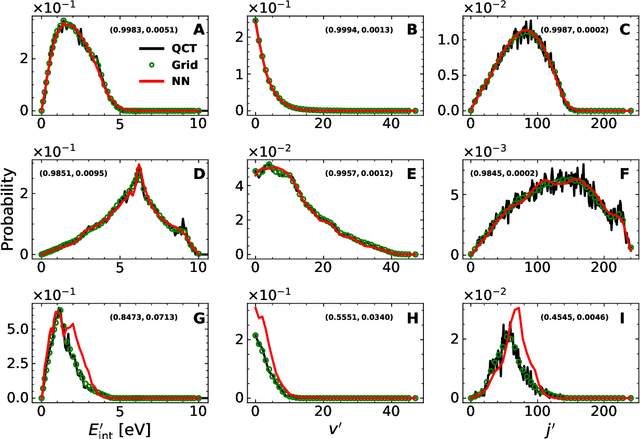
A machine learned (ML) model for predicting product state distributions from specific initial states (state-to-distribution or STD) for reactive atom-diatom collisions is presented and quantitatively tested for the N($^4$S)+O$_{2}$(X$^3 \Sigma_{\rm g}^{-}$) $\rightarrow$ NO(X$^2\Pi$) +O($^3$P) reaction. The reference data set for training the neural network (NN) consists of final state distributions determined from explicit quasi-classical trajectory (QCT) simulations for $\sim 2000$ initial conditions. Overall, the prediction accuracy as quantified by the root-mean-squared difference $(\sim 0.003)$ and the $R^2$ $(\sim 0.99)$ between the reference QCT and predictions of the STD model is high for the test set and off-grid state specific initial conditions and for initial conditions drawn from reactant state distributions characterized by translational, rotational and vibrational temperatures. Compared with a more coarse grained distribution-to-distribution (DTD) model evaluated on the same initial state distributions, the STD model shows comparable performance with the additional benefit of the state resolution in the reactant preparation. Starting from specific initial states also leads to a more diverse range of final state distributions which requires a more expressive neural network to be used compared with DTD. Direct comparison between explicit QCT simulations, the STD model, and the widely used Larsen-Borgnakke (LB) model shows that the STD model is quantitative whereas the LB model is qualitative at best for rotational distributions $P(j')$ and fails for vibrational distributions $P(v')$. As such the STD model can be well-suited for simulating nonequilibrium high-speed flows, e.g., using the direct simulation Monte Carlo method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge