${\it Asparagus}$: A Toolkit for Autonomous, User-Guided Construction of Machine-Learned Potential Energy Surfaces

With the establishment of machine learning (ML) techniques in the scientific community, the construction of ML potential energy surfaces (ML-PES) has become a standard process in physics and chemistry. So far, improvements in the construction of ML-PES models have been conducted independently, creating an initial hurdle for new users to overcome and complicating the reproducibility of results. Aiming to reduce the bar for the extensive use of ML-PES, we introduce ${\it Asparagus}$, a software package encompassing the different parts into one coherent implementation that allows an autonomous, user-guided construction of ML-PES models. ${\it Asparagus}$ combines capabilities of initial data sampling with interfaces to ${\it ab initio}$ calculation programs, ML model training, as well as model evaluation and its application within other codes such as ASE or CHARMM. The functionalities of the code are illustrated in different examples, including the dynamics of small molecules, the representation of reactive potentials in organometallic compounds, and atom diffusion on periodic surface structures. The modular framework of ${\it Asparagus}$ is designed to allow simple implementations of further ML-related methods and models to provide constant user-friendly access to state-of-the-art ML techniques.

Outlier-Detection for Reactive Machine Learned Potential Energy Surfaces

Uncertainty quantification (UQ) to detect samples with large expected errors (outliers) is applied to reactive molecular potential energy surfaces (PESs). Three methods - Ensembles, Deep Evidential Regression (DER), and Gaussian Mixture Models (GMM) - were applied to the H-transfer reaction between ${\it syn-}$Criegee and vinyl hydroxyperoxide. The results indicate that ensemble models provide the best results for detecting outliers, followed by GMM. For example, from a pool of 1000 structures with the largest uncertainty, the detection quality for outliers is $\sim 90$ \% and $\sim 50$ \%, respectively, if 25 or 1000 structures with large errors are sought. On the contrary, the limitations of the statistical assumptions of DER greatly impacted its prediction capabilities. Finally, a structure-based indicator was found to be correlated with large average error, which may help to rapidly classify new structures into those that provide an advantage for refining the neural network.

Machine Learning Product State Distributions from Initial Reactant States for a Reactive Atom-Diatom Collision System

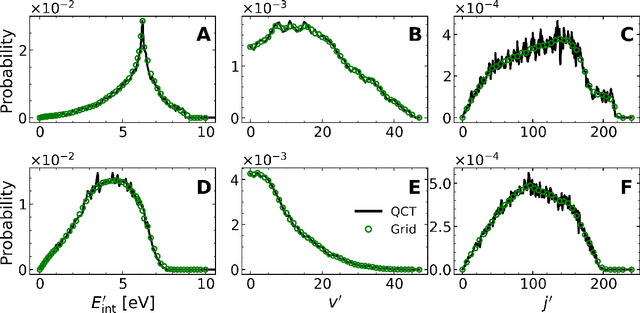
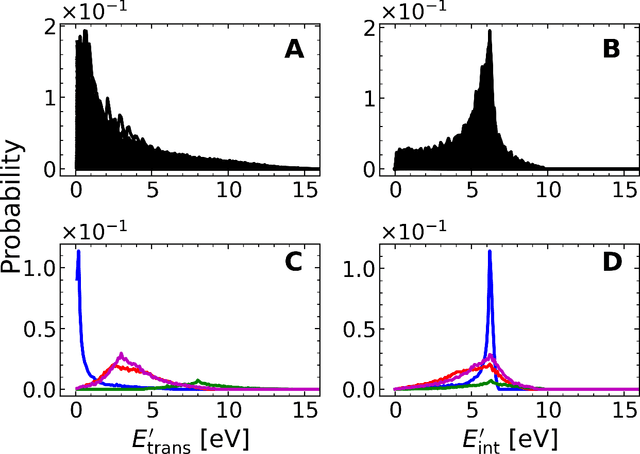
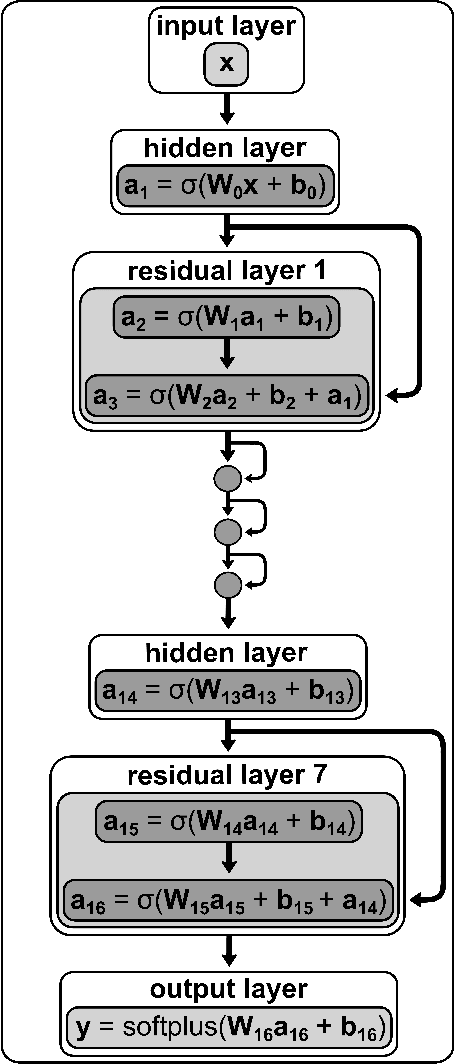
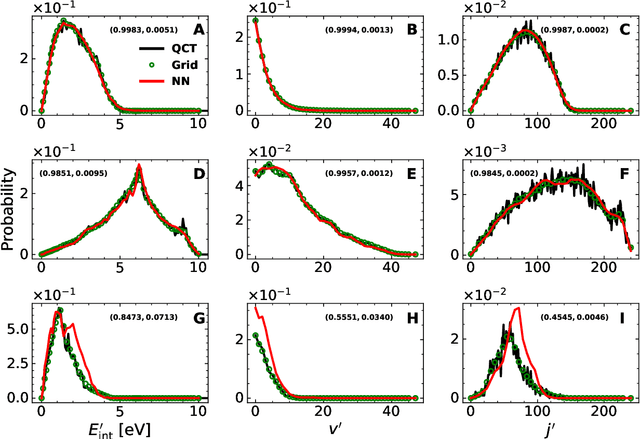
A machine learned (ML) model for predicting product state distributions from specific initial states (state-to-distribution or STD) for reactive atom-diatom collisions is presented and quantitatively tested for the N($^4$S)+O$_{2}$(X$^3 \Sigma_{\rm g}^{-}$) $\rightarrow$ NO(X$^2\Pi$) +O($^3$P) reaction. The reference data set for training the neural network (NN) consists of final state distributions determined from explicit quasi-classical trajectory (QCT) simulations for $\sim 2000$ initial conditions. Overall, the prediction accuracy as quantified by the root-mean-squared difference $(\sim 0.003)$ and the $R^2$ $(\sim 0.99)$ between the reference QCT and predictions of the STD model is high for the test set and off-grid state specific initial conditions and for initial conditions drawn from reactant state distributions characterized by translational, rotational and vibrational temperatures. Compared with a more coarse grained distribution-to-distribution (DTD) model evaluated on the same initial state distributions, the STD model shows comparable performance with the additional benefit of the state resolution in the reactant preparation. Starting from specific initial states also leads to a more diverse range of final state distributions which requires a more expressive neural network to be used compared with DTD. Direct comparison between explicit QCT simulations, the STD model, and the widely used Larsen-Borgnakke (LB) model shows that the STD model is quantitative whereas the LB model is qualitative at best for rotational distributions $P(j')$ and fails for vibrational distributions $P(v')$. As such the STD model can be well-suited for simulating nonequilibrium high-speed flows, e.g., using the direct simulation Monte Carlo method.