End-to-end metasurface design for temperature imaging via broadband Planck-radiation regression

We present a theoretical framework for temperature imaging from long-wavelength infrared thermal radiation (e.g. 8-12 $\mu$m) through the end-to-end design of a metasurface-optics frontend and a computational-reconstruction backend. We introduce a new nonlinear reconstruction algorithm, ``Planck regression," that reconstructs the temperature map from a grayscale sensor image, even in the presence of severe chromatic aberration, by exploiting blackbody and optical physics particular to thermal imaging. We combine this algorithm with an end-to-end approach that optimizes a manufacturable, single-layer metasurface to yield the most accurate reconstruction. Our designs demonstrate high-quality, noise-robust reconstructions of arbitrary temperature maps (including completely random images) in simulations of an ultra-compact thermal-imaging device. We also show that Planck regression is much more generalizable to arbitrary images than a straightforward neural-network reconstruction, which requires a large training set of domain-specific images.

Differentiating Metropolis-Hastings to Optimize Intractable Densities

We develop an algorithm for automatic differentiation of Metropolis-Hastings samplers, allowing us to differentiate through probabilistic inference, even if the model has discrete components within it. Our approach fuses recent advances in stochastic automatic differentiation with traditional Markov chain coupling schemes, providing an unbiased and low-variance gradient estimator. This allows us to apply gradient-based optimization to objectives expressed as expectations over intractable target densities. We demonstrate our approach by finding an ambiguous observation in a Gaussian mixture model and by maximizing the specific heat in an Ising model.

Transcending shift-invariance in the paraxial regime via end-to-end inverse design of freeform nanophotonics

Traditional optical elements and conventional metasurfaces obey shift-invariance in the paraxial regime. For imaging systems obeying paraxial shift-invariance, a small shift in input angle causes a corresponding shift in the sensor image. Shift-invariance has deep implications for the design and functionality of optical devices, such as the necessity of free space between components (as in compound objectives made of several curved surfaces). We present a method for nanophotonic inverse design of compact imaging systems whose resolution is not constrained by paraxial shift-invariance. Our method is end-to-end, in that it integrates density-based full-Maxwell topology optimization with a fully iterative elastic-net reconstruction algorithm. By the design of nanophotonic structures that scatter light in a non-shift-invariant manner, our optimized nanophotonic imaging system overcomes the limitations of paraxial shift-invariance, achieving accurate, noise-robust image reconstruction beyond shift-invariant resolution.

Automatic Differentiation of Programs with Discrete Randomness

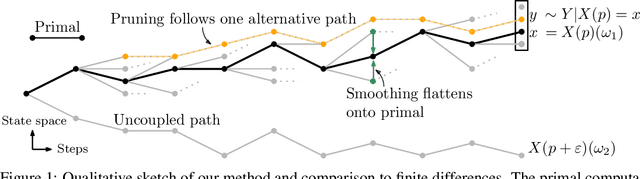
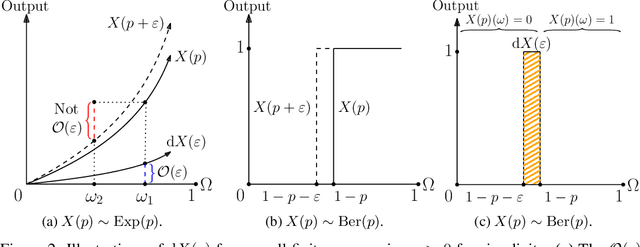
Automatic differentiation (AD), a technique for constructing new programs which compute the derivative of an original program, has become ubiquitous throughout scientific computing and deep learning due to the improved performance afforded by gradient-based optimization. However, AD systems have been restricted to the subset of programs that have a continuous dependence on parameters. Programs that have discrete stochastic behaviors governed by distribution parameters, such as flipping a coin with probability $p$ of being heads, pose a challenge to these systems because the connection between the result (heads vs tails) and the parameters ($p$) is fundamentally discrete. In this paper we develop a new reparameterization-based methodology that allows for generating programs whose expectation is the derivative of the expectation of the original program. We showcase how this method gives an unbiased and low-variance estimator which is as automated as traditional AD mechanisms. We demonstrate unbiased forward-mode AD of discrete-time Markov chains, agent-based models such as Conway's Game of Life, and unbiased reverse-mode AD of a particle filter. Our code is available at https://github.com/gaurav-arya/StochasticAD.jl.

End-to-End Optimization of Metasurfaces for Imaging with Compressed Sensing

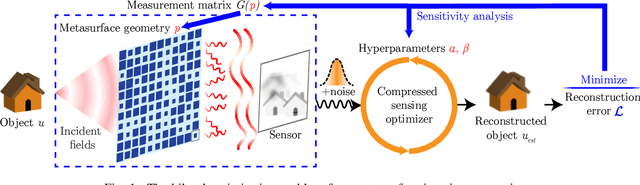
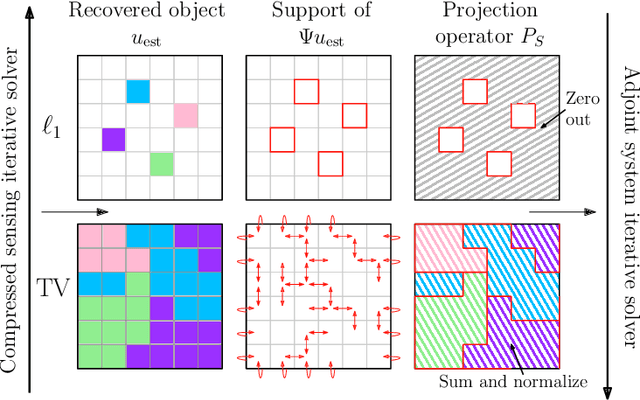
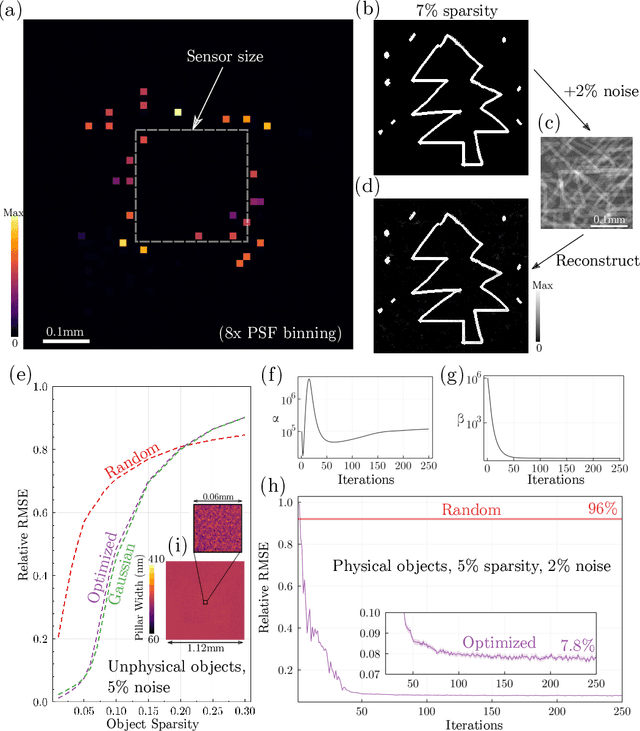
We present a method for the end-to-end optimization of computational imaging systems that reconstruct targets using compressed sensing. Using an adjoint analysis of the Karush-Kuhn-Tucker conditions, we incorporate a fully iterative compressed sensing algorithm that solves an $\ell_1$-regularized minimization problem, nested within the end-to-end optimization pipeline. We apply this method to jointly optimize the optical and computational parameters of metasurface-based imaging systems for underdetermined recovery problems. This allows us to investigate the interplay of nanoscale optics with the design goals of compressed sensing imaging systems. Our optimized metasurface imaging systems are robust to noise, significantly improving over random scattering surfaces and approaching the ideal compressed sensing performance of a Gaussian matrix.