End-to-end metasurface design for temperature imaging via broadband Planck-radiation regression

We present a theoretical framework for temperature imaging from long-wavelength infrared thermal radiation (e.g. 8-12 $\mu$m) through the end-to-end design of a metasurface-optics frontend and a computational-reconstruction backend. We introduce a new nonlinear reconstruction algorithm, ``Planck regression," that reconstructs the temperature map from a grayscale sensor image, even in the presence of severe chromatic aberration, by exploiting blackbody and optical physics particular to thermal imaging. We combine this algorithm with an end-to-end approach that optimizes a manufacturable, single-layer metasurface to yield the most accurate reconstruction. Our designs demonstrate high-quality, noise-robust reconstructions of arbitrary temperature maps (including completely random images) in simulations of an ultra-compact thermal-imaging device. We also show that Planck regression is much more generalizable to arbitrary images than a straightforward neural-network reconstruction, which requires a large training set of domain-specific images.

Transcending shift-invariance in the paraxial regime via end-to-end inverse design of freeform nanophotonics

Traditional optical elements and conventional metasurfaces obey shift-invariance in the paraxial regime. For imaging systems obeying paraxial shift-invariance, a small shift in input angle causes a corresponding shift in the sensor image. Shift-invariance has deep implications for the design and functionality of optical devices, such as the necessity of free space between components (as in compound objectives made of several curved surfaces). We present a method for nanophotonic inverse design of compact imaging systems whose resolution is not constrained by paraxial shift-invariance. Our method is end-to-end, in that it integrates density-based full-Maxwell topology optimization with a fully iterative elastic-net reconstruction algorithm. By the design of nanophotonic structures that scatter light in a non-shift-invariant manner, our optimized nanophotonic imaging system overcomes the limitations of paraxial shift-invariance, achieving accurate, noise-robust image reconstruction beyond shift-invariant resolution.

A Methodological Framework for the Comparative Evaluation of Multiple Imputation Methods: Multiple Imputation of Race, Ethnicity and Body Mass Index in the U.S. National COVID Cohort Collaborative

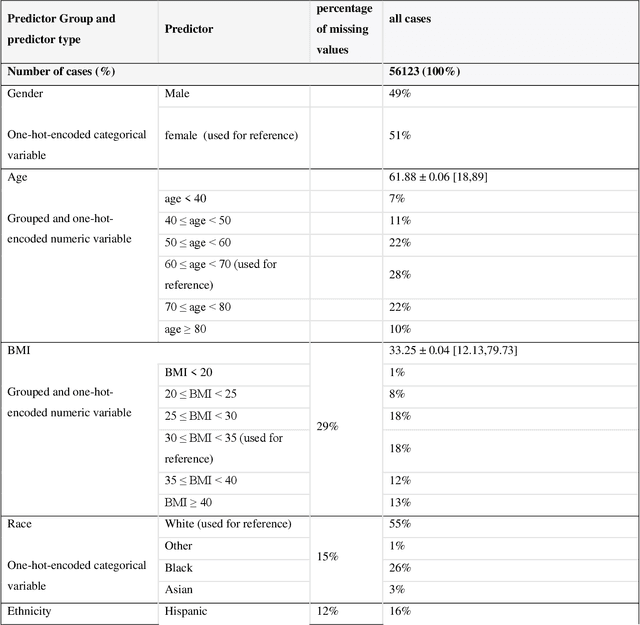
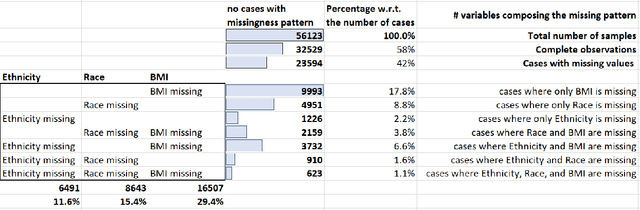
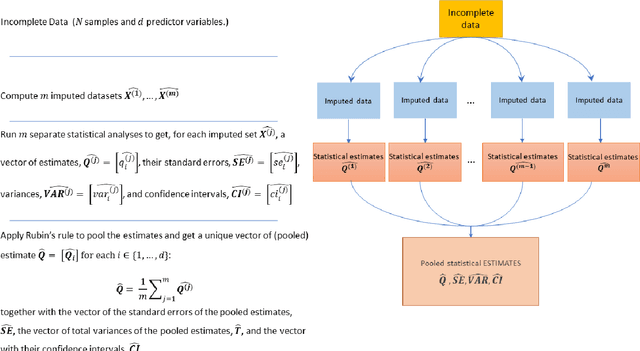
While electronic health records are a rich data source for biomedical research, these systems are not implemented uniformly across healthcare settings and significant data may be missing due to healthcare fragmentation and lack of interoperability between siloed electronic health records. Considering that the deletion of cases with missing data may introduce severe bias in the subsequent analysis, several authors prefer applying a multiple imputation strategy to recover the missing information. Unfortunately, although several literature works have documented promising results by using any of the different multiple imputation algorithms that are now freely available for research, there is no consensus on which MI algorithm works best. Beside the choice of the MI strategy, the choice of the imputation algorithm and its application settings are also both crucial and challenging. In this paper, inspired by the seminal works of Rubin and van Buuren, we propose a methodological framework that may be applied to evaluate and compare several multiple imputation techniques, with the aim to choose the most valid for computing inferences in a clinical research work. Our framework has been applied to validate, and extend on a larger cohort, the results we presented in a previous literature study, where we evaluated the influence of crucial patients' descriptors and COVID-19 severity in patients with type 2 diabetes mellitus whose data is provided by the National COVID Cohort Collaborative Enclave.

Inverse-Designed Meta-Optics with Spectral-Spatial Engineered Response to Mimic Color Perception

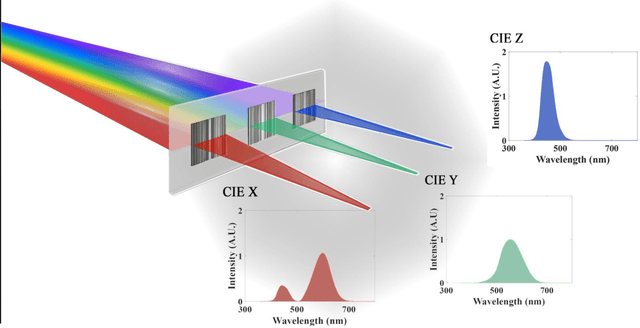
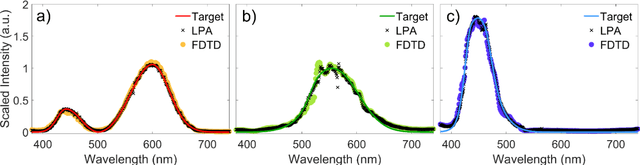
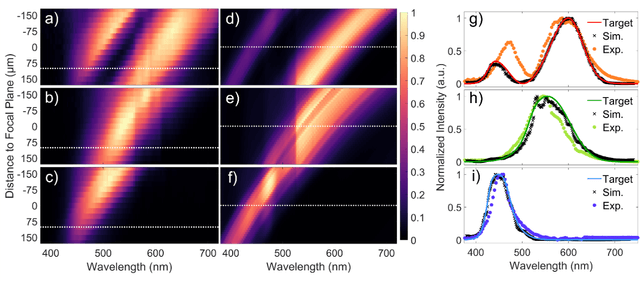
Meta-optics have rapidly become a major research field within the optics and photonics community, strongly driven by the seemingly limitless opportunities made possible by controlling optical wavefronts through interaction with arrays of sub-wavelength scatterers. As more and more modalities are explored, the design strategies to achieve desired functionalities become increasingly demanding, necessitating more advanced design techniques. Herein, the inverse-design approach is utilized to create a set of single-layer meta-optics that simultaneously focus light and shape the spectra of focused light without using any filters. Thus, both spatial and spectral properties of the meta-optics are optimized, resulting in spectra that mimic the color matching functions of the CIE 1931 XYZ color space, which links the distributions of wavelengths in light and the color perception of a human eye. Experimental demonstrations of these meta-optics show qualitative agreement with the theoretical predictions and help elucidate the focusing mechanism of these devices.

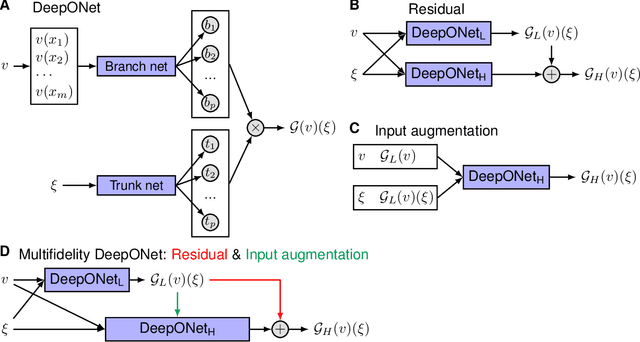
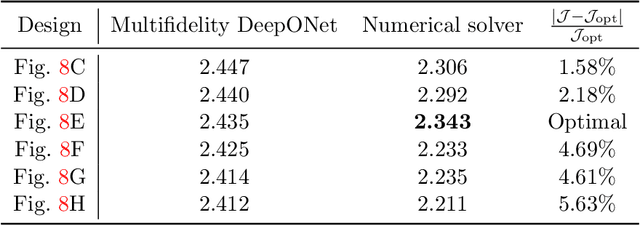
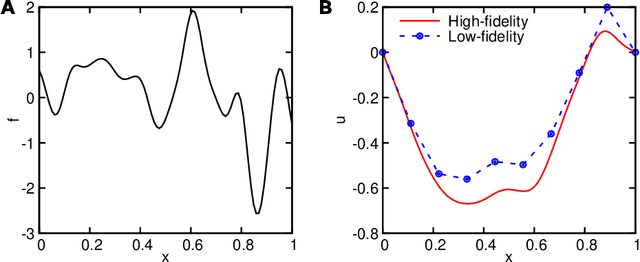
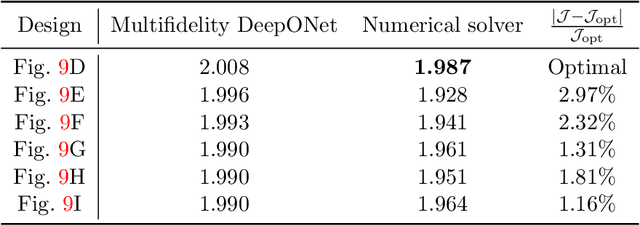
Multifidelity deep neural operators for efficient learning of partial differential equations with application to fast inverse design of nanoscale heat transport

Deep neural operators can learn operators mapping between infinite-dimensional function spaces via deep neural networks and have become an emerging paradigm of scientific machine learning. However, training neural operators usually requires a large amount of high-fidelity data, which is often difficult to obtain in real engineering problems. Here, we address this challenge by using multifidelity learning, i.e., learning from multifidelity datasets. We develop a multifidelity neural operator based on a deep operator network (DeepONet). A multifidelity DeepONet includes two standard DeepONets coupled by residual learning and input augmentation. Multifidelity DeepONet significantly reduces the required amount of high-fidelity data and achieves one order of magnitude smaller error when using the same amount of high-fidelity data. We apply a multifidelity DeepONet to learn the phonon Boltzmann transport equation (BTE), a framework to compute nanoscale heat transport. By combining a trained multifidelity DeepONet with genetic algorithm or topology optimization, we demonstrate a fast solver for the inverse design of BTE problems.

End-to-End Optimization of Metasurfaces for Imaging with Compressed Sensing

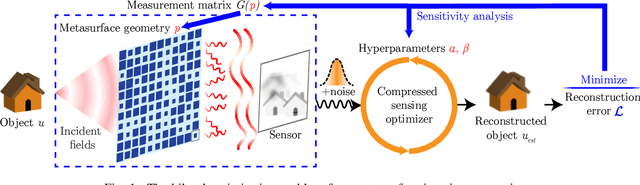
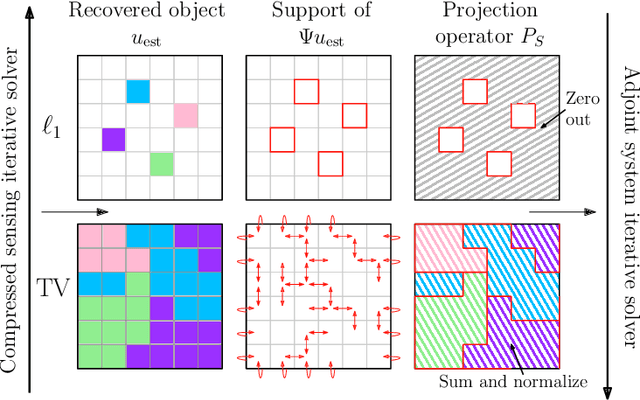
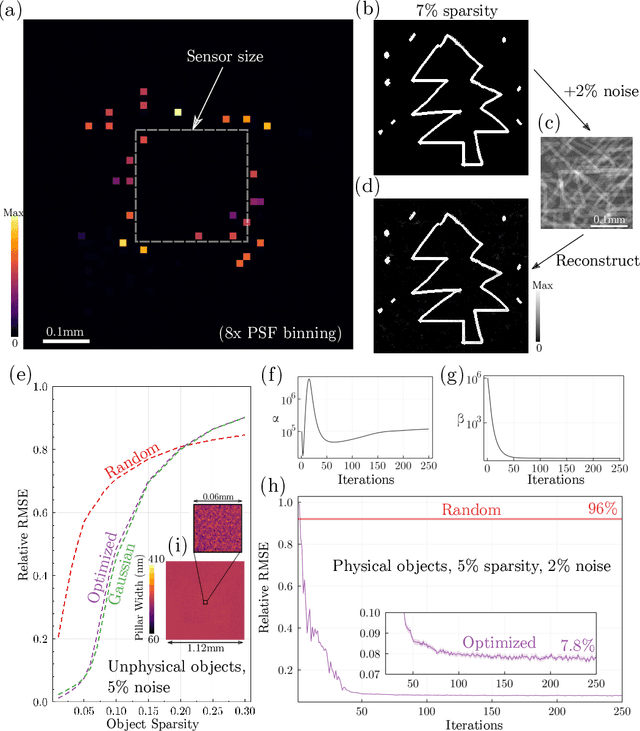
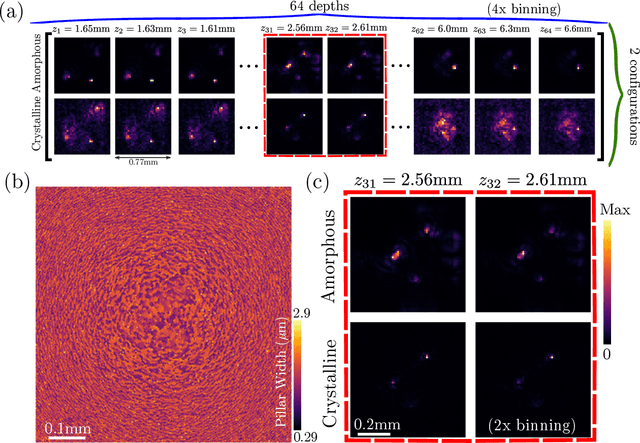
We present a method for the end-to-end optimization of computational imaging systems that reconstruct targets using compressed sensing. Using an adjoint analysis of the Karush-Kuhn-Tucker conditions, we incorporate a fully iterative compressed sensing algorithm that solves an $\ell_1$-regularized minimization problem, nested within the end-to-end optimization pipeline. We apply this method to jointly optimize the optical and computational parameters of metasurface-based imaging systems for underdetermined recovery problems. This allows us to investigate the interplay of nanoscale optics with the design goals of compressed sensing imaging systems. Our optimized metasurface imaging systems are robust to noise, significantly improving over random scattering surfaces and approaching the ideal compressed sensing performance of a Gaussian matrix.

Physics-enhanced deep surrogates for PDEs

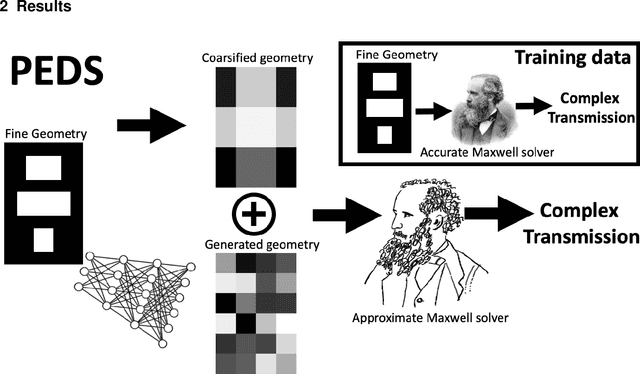
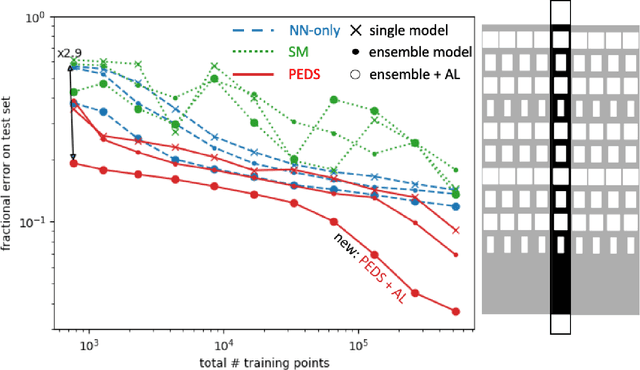
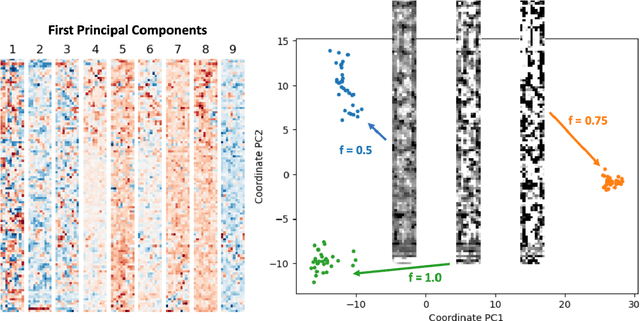
We present a "physics-enhanced deep-surrogate ("PEDS") approach towards developing fast surrogate models for complex physical systems described by partial differential equations (PDEs) and similar models: we show how to combine a low-fidelity "coarse" solver with a neural network that generates "coarsified'' inputs, trained end-to-end to globally match the output of an expensive high-fidelity numerical solver. In this way, by incorporating limited physical knowledge in the form of the low-fidelity model, we find that a PEDS surrogate can be trained with at least $\sim 10\times$ less data than a "black-box'' neural network for the same accuracy. Asymptotically, PEDS appears to learn with a steeper power law than black-box surrogates, and benefits even further when combined with active learning. We demonstrate feasibility and benefit of the proposed approach by using an example problem in electromagnetic scattering that appears in the design of optical metamaterials.

Physics-informed neural networks with hard constraints for inverse design

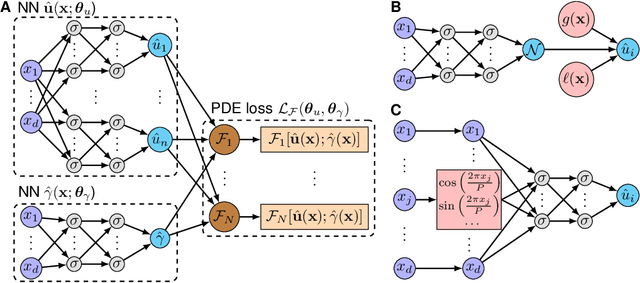
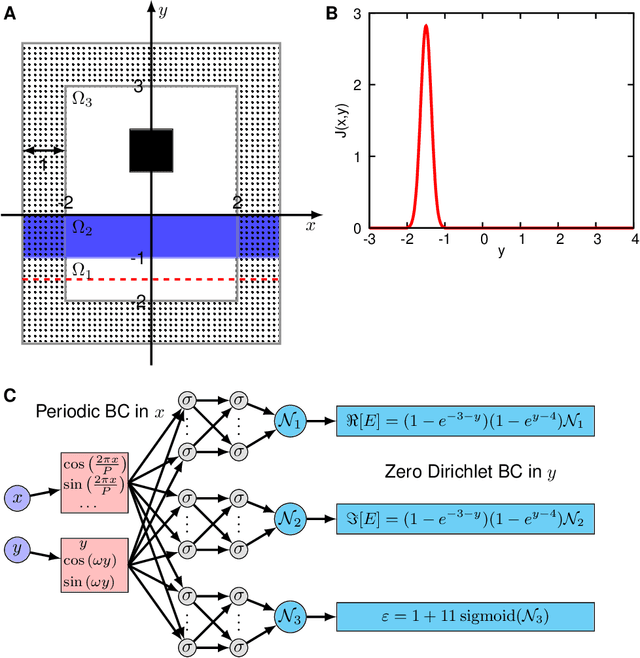
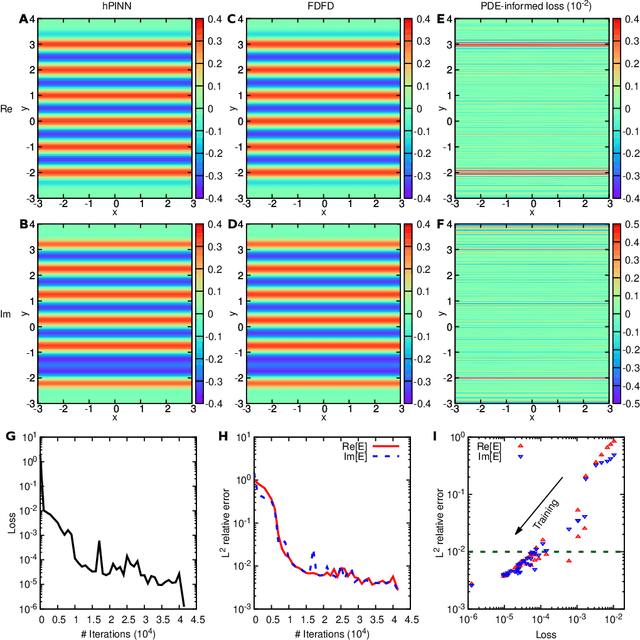
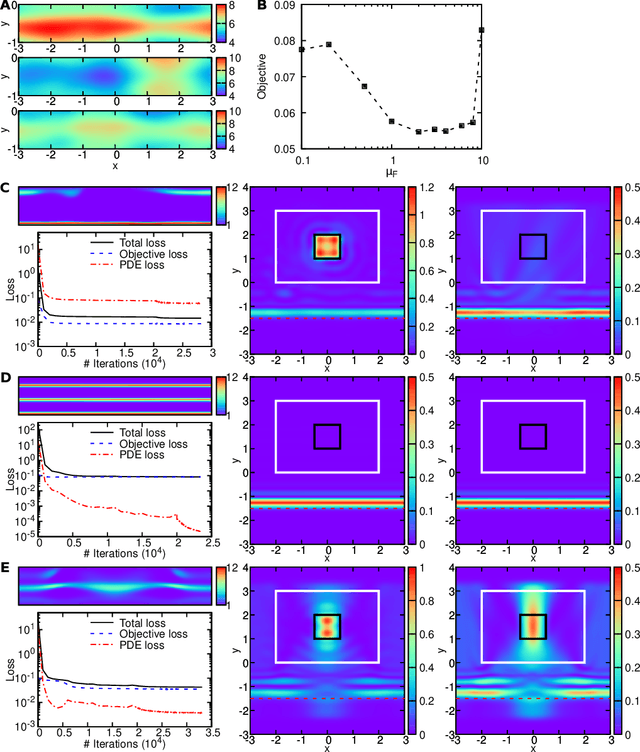
Inverse design arises in a variety of areas in engineering such as acoustic, mechanics, thermal/electronic transport, electromagnetism, and optics. Topology optimization is a major form of inverse design, where we optimize a designed geometry to achieve targeted properties and the geometry is parameterized by a density function. This optimization is challenging, because it has a very high dimensionality and is usually constrained by partial differential equations (PDEs) and additional inequalities. Here, we propose a new deep learning method -- physics-informed neural networks with hard constraints (hPINNs) -- for solving topology optimization. hPINN leverages the recent development of PINNs for solving PDEs, and thus does not rely on any numerical PDE solver. However, all the constraints in PINNs are soft constraints, and hence we impose hard constraints by using the penalty method and the augmented Lagrangian method. We demonstrate the effectiveness of hPINN for a holography problem in optics and a fluid problem of Stokes flow. We achieve the same objective as conventional PDE-constrained optimization methods based on adjoint methods and numerical PDE solvers, but find that the design obtained from hPINN is often simpler and smoother for problems whose solution is not unique. Moreover, the implementation of inverse design with hPINN can be easier than that of conventional methods.

Active learning of deep surrogates for PDEs: Application to metasurface design

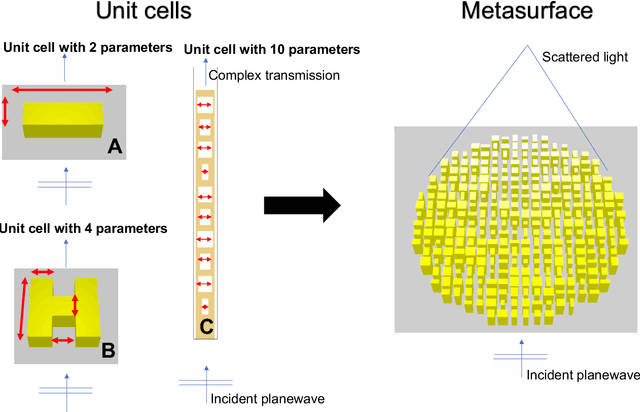
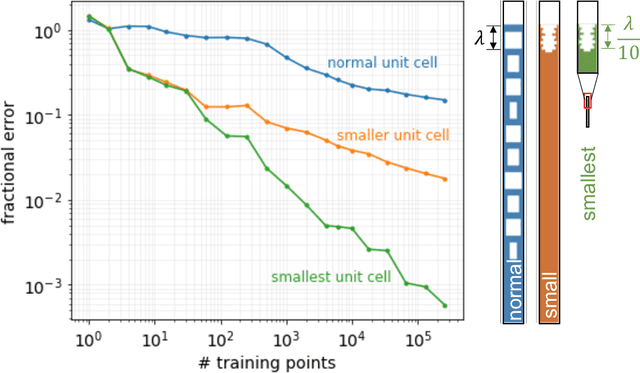
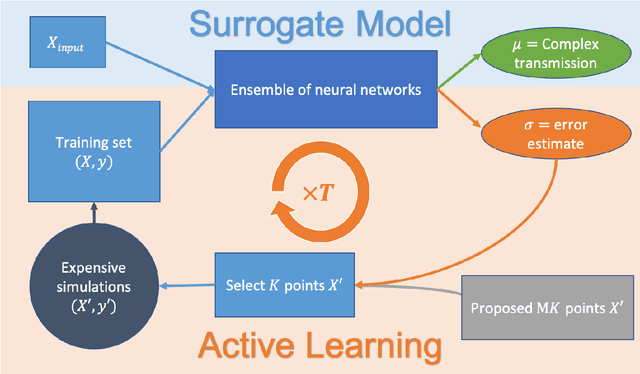
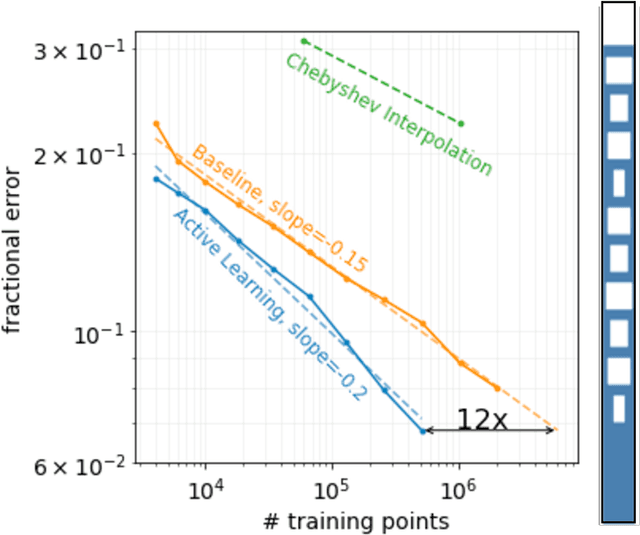
Surrogate models for partial-differential equations are widely used in the design of meta-materials to rapidly evaluate the behavior of composable components. However, the training cost of accurate surrogates by machine learning can rapidly increase with the number of variables. For photonic-device models, we find that this training becomes especially challenging as design regions grow larger than the optical wavelength. We present an active learning algorithm that reduces the number of training points by more than an order of magnitude for a neural-network surrogate model of optical-surface components compared to random samples. Results show that the surrogate evaluation is over two orders of magnitude faster than a direct solve, and we demonstrate how this can be exploited to accelerate large-scale engineering optimization.