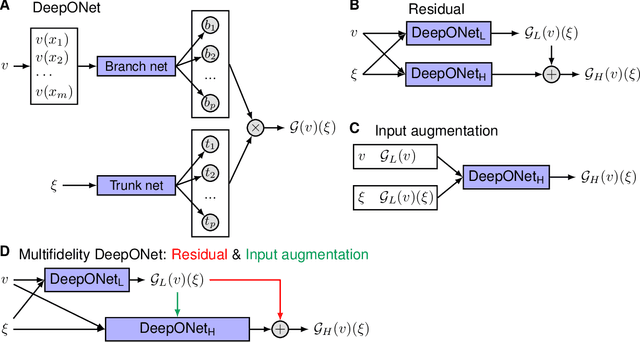
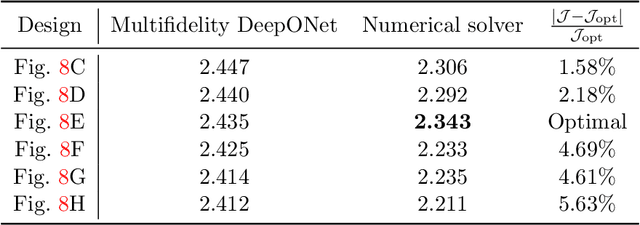
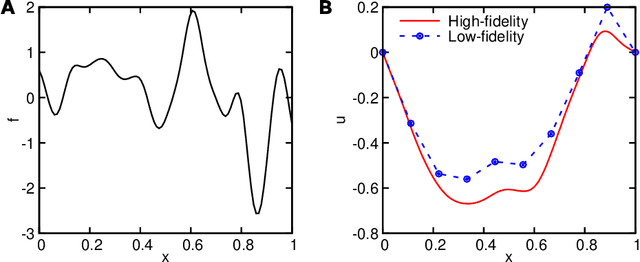
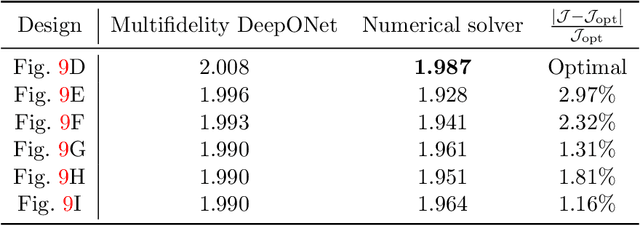
Multifidelity deep neural operators for efficient learning of partial differential equations with application to fast inverse design of nanoscale heat transport

Deep neural operators can learn operators mapping between infinite-dimensional function spaces via deep neural networks and have become an emerging paradigm of scientific machine learning. However, training neural operators usually requires a large amount of high-fidelity data, which is often difficult to obtain in real engineering problems. Here, we address this challenge by using multifidelity learning, i.e., learning from multifidelity datasets. We develop a multifidelity neural operator based on a deep operator network (DeepONet). A multifidelity DeepONet includes two standard DeepONets coupled by residual learning and input augmentation. Multifidelity DeepONet significantly reduces the required amount of high-fidelity data and achieves one order of magnitude smaller error when using the same amount of high-fidelity data. We apply a multifidelity DeepONet to learn the phonon Boltzmann transport equation (BTE), a framework to compute nanoscale heat transport. By combining a trained multifidelity DeepONet with genetic algorithm or topology optimization, we demonstrate a fast solver for the inverse design of BTE problems.

Physics-informed neural networks with hard constraints for inverse design

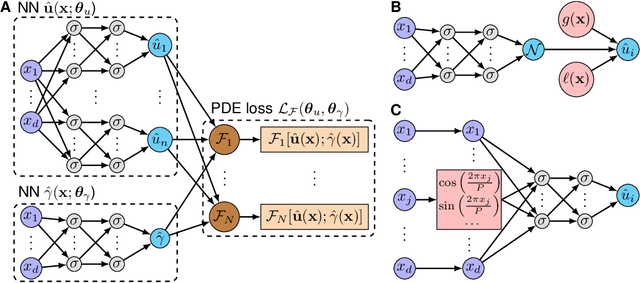
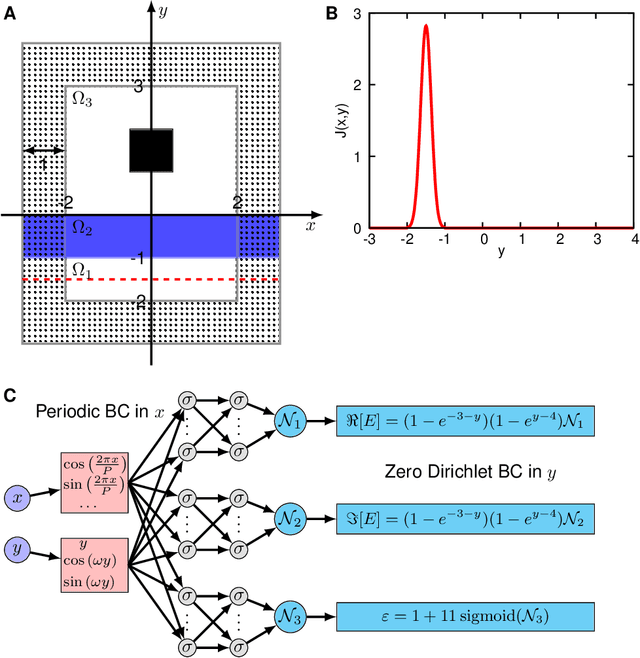
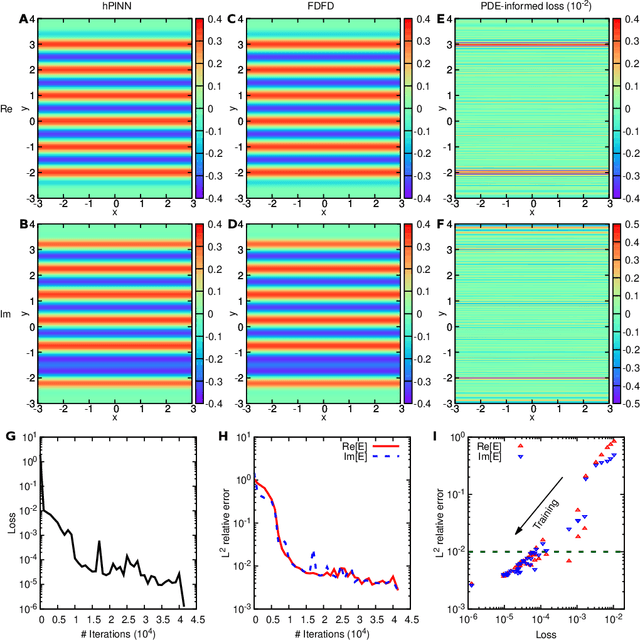
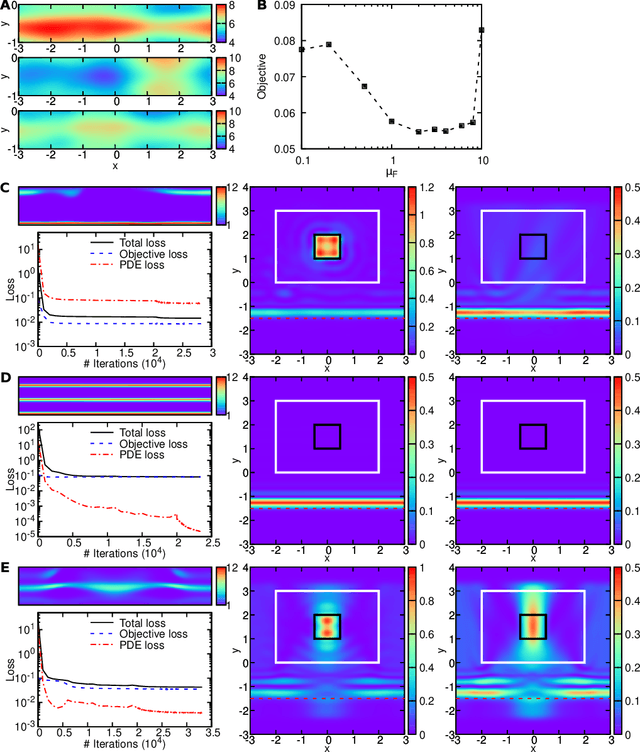
Inverse design arises in a variety of areas in engineering such as acoustic, mechanics, thermal/electronic transport, electromagnetism, and optics. Topology optimization is a major form of inverse design, where we optimize a designed geometry to achieve targeted properties and the geometry is parameterized by a density function. This optimization is challenging, because it has a very high dimensionality and is usually constrained by partial differential equations (PDEs) and additional inequalities. Here, we propose a new deep learning method -- physics-informed neural networks with hard constraints (hPINNs) -- for solving topology optimization. hPINN leverages the recent development of PINNs for solving PDEs, and thus does not rely on any numerical PDE solver. However, all the constraints in PINNs are soft constraints, and hence we impose hard constraints by using the penalty method and the augmented Lagrangian method. We demonstrate the effectiveness of hPINN for a holography problem in optics and a fluid problem of Stokes flow. We achieve the same objective as conventional PDE-constrained optimization methods based on adjoint methods and numerical PDE solvers, but find that the design obtained from hPINN is often simpler and smoother for problems whose solution is not unique. Moreover, the implementation of inverse design with hPINN can be easier than that of conventional methods.