Physics-enhanced deep surrogates for PDEs

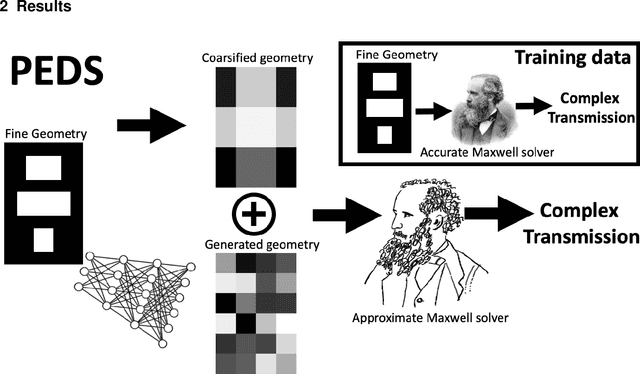
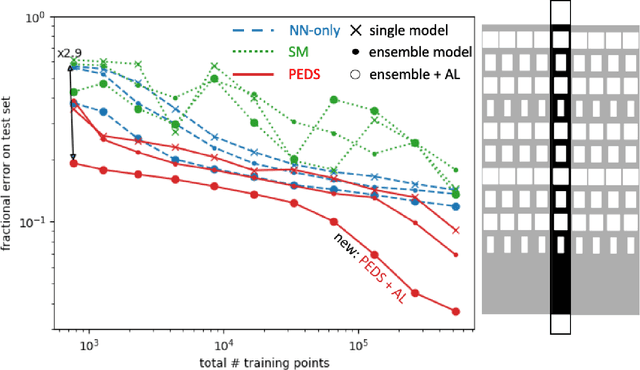
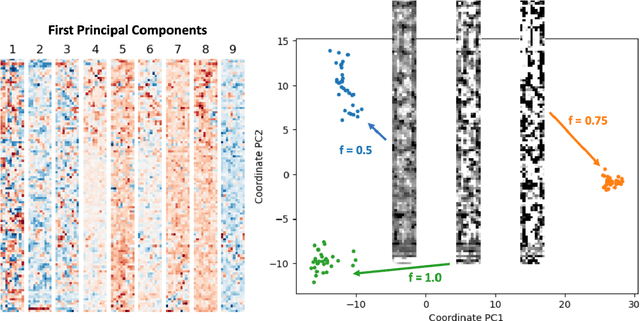
We present a "physics-enhanced deep-surrogate ("PEDS") approach towards developing fast surrogate models for complex physical systems described by partial differential equations (PDEs) and similar models: we show how to combine a low-fidelity "coarse" solver with a neural network that generates "coarsified'' inputs, trained end-to-end to globally match the output of an expensive high-fidelity numerical solver. In this way, by incorporating limited physical knowledge in the form of the low-fidelity model, we find that a PEDS surrogate can be trained with at least $\sim 10\times$ less data than a "black-box'' neural network for the same accuracy. Asymptotically, PEDS appears to learn with a steeper power law than black-box surrogates, and benefits even further when combined with active learning. We demonstrate feasibility and benefit of the proposed approach by using an example problem in electromagnetic scattering that appears in the design of optical metamaterials.