A Practitioner's Guide to Bayesian Inference in Pharmacometrics using Pumas

This paper provides a comprehensive tutorial for Bayesian practitioners in pharmacometrics using Pumas workflows. We start by giving a brief motivation of Bayesian inference for pharmacometrics highlighting limitations in existing software that Pumas addresses. We then follow by a description of all the steps of a standard Bayesian workflow for pharmacometrics using code snippets and examples. This includes: model definition, prior selection, sampling from the posterior, prior and posterior simulations and predictions, counter-factual simulations and predictions, convergence diagnostics, visual predictive checks, and finally model comparison with cross-validation. Finally, the background and intuition behind many advanced concepts in Bayesian statistics are explained in simple language. This includes many important ideas and precautions that users need to keep in mind when performing Bayesian analysis. Many of the algorithms, codes, and ideas presented in this paper are highly applicable to clinical research and statistical learning at large but we chose to focus our discussions on pharmacometrics in this paper to have a narrower scope in mind and given the nature of Pumas as a software primarily for pharmacometricians.

Efficient hybrid modeling and sorption model discovery for non-linear advection-diffusion-sorption systems: A systematic scientific machine learning approach

This study presents a systematic machine learning approach for creating efficient hybrid models and discovering sorption uptake models in non-linear advection-diffusion-sorption systems. It demonstrates an effective method to train these complex systems using gradient based optimizers, adjoint sensitivity analysis, and JIT-compiled vector Jacobian products, combined with spatial discretization and adaptive integrators. Sparse and symbolic regression were employed to identify missing functions in the artificial neural network. The robustness of the proposed method was tested on an in-silico data set of noisy breakthrough curve observations of fixed-bed adsorption, resulting in a well-fitted hybrid model. The study successfully reconstructed sorption uptake kinetics using sparse and symbolic regression, and accurately predicted breakthrough curves using identified polynomials, highlighting the potential of the proposed framework for discovering sorption kinetic law structures.

Locally Regularized Neural Differential Equations: Some Black Boxes Were Meant to Remain Closed!

Implicit layer deep learning techniques, like Neural Differential Equations, have become an important modeling framework due to their ability to adapt to new problems automatically. Training a neural differential equation is effectively a search over a space of plausible dynamical systems. However, controlling the computational cost for these models is difficult since it relies on the number of steps the adaptive solver takes. Most prior works have used higher-order methods to reduce prediction timings while greatly increasing training time or reducing both training and prediction timings by relying on specific training algorithms, which are harder to use as a drop-in replacement due to strict requirements on automatic differentiation. In this manuscript, we use internal cost heuristics of adaptive differential equation solvers at stochastic time points to guide the training toward learning a dynamical system that is easier to integrate. We "close the black-box" and allow the use of our method with any adjoint technique for gradient calculations of the differential equation solution. We perform experimental studies to compare our method to global regularization to show that we attain similar performance numbers without compromising the flexibility of implementation on ordinary differential equations (ODEs) and stochastic differential equations (SDEs). We develop two sampling strategies to trade off between performance and training time. Our method reduces the number of function evaluations to 0.556-0.733x and accelerates predictions by 1.3-2x.

Differentiable modeling to unify machine learning and physical models and advance Geosciences

Process-Based Modeling (PBM) and Machine Learning (ML) are often perceived as distinct paradigms in the geosciences. Here we present differentiable geoscientific modeling as a powerful pathway toward dissolving the perceived barrier between them and ushering in a paradigm shift. For decades, PBM offered benefits in interpretability and physical consistency but struggled to efficiently leverage large datasets. ML methods, especially deep networks, presented strong predictive skills yet lacked the ability to answer specific scientific questions. While various methods have been proposed for ML-physics integration, an important underlying theme -- differentiable modeling -- is not sufficiently recognized. Here we outline the concepts, applicability, and significance of differentiable geoscientific modeling (DG). "Differentiable" refers to accurately and efficiently calculating gradients with respect to model variables, critically enabling the learning of high-dimensional unknown relationships. DG refers to a range of methods connecting varying amounts of prior knowledge to neural networks and training them together, capturing a different scope than physics-guided machine learning and emphasizing first principles. Preliminary evidence suggests DG offers better interpretability and causality than ML, improved generalizability and extrapolation capability, and strong potential for knowledge discovery, while approaching the performance of purely data-driven ML. DG models require less training data while scaling favorably in performance and efficiency with increasing amounts of data. With DG, geoscientists may be better able to frame and investigate questions, test hypotheses, and discover unrecognized linkages.

Automatic Differentiation of Programs with Discrete Randomness

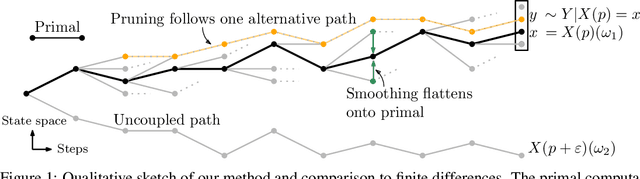
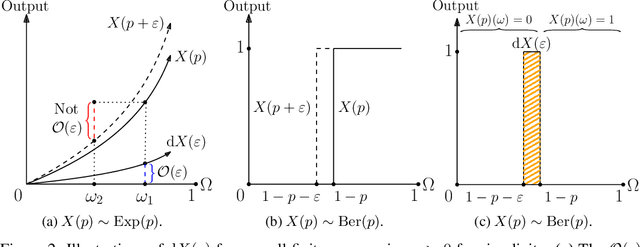
Automatic differentiation (AD), a technique for constructing new programs which compute the derivative of an original program, has become ubiquitous throughout scientific computing and deep learning due to the improved performance afforded by gradient-based optimization. However, AD systems have been restricted to the subset of programs that have a continuous dependence on parameters. Programs that have discrete stochastic behaviors governed by distribution parameters, such as flipping a coin with probability $p$ of being heads, pose a challenge to these systems because the connection between the result (heads vs tails) and the parameters ($p$) is fundamentally discrete. In this paper we develop a new reparameterization-based methodology that allows for generating programs whose expectation is the derivative of the expectation of the original program. We showcase how this method gives an unbiased and low-variance estimator which is as automated as traditional AD mechanisms. We demonstrate unbiased forward-mode AD of discrete-time Markov chains, agent-based models such as Conway's Game of Life, and unbiased reverse-mode AD of a particle filter. Our code is available at https://github.com/gaurav-arya/StochasticAD.jl.

ReservoirComputing.jl: An Efficient and Modular Library for Reservoir Computing Models

We introduce ReservoirComputing.jl, an open source Julia library for reservoir computing models. The software offers a great number of algorithms presented in the literature, and allows to expand on them with both internal and external tools in a simple way. The implementation is highly modular, fast and comes with a comprehensive documentation, which includes reproduced experiments from literature. The code and documentation are hosted on Github under an MIT license https://github.com/SciML/ReservoirComputing.jl.

Physics-enhanced deep surrogates for PDEs

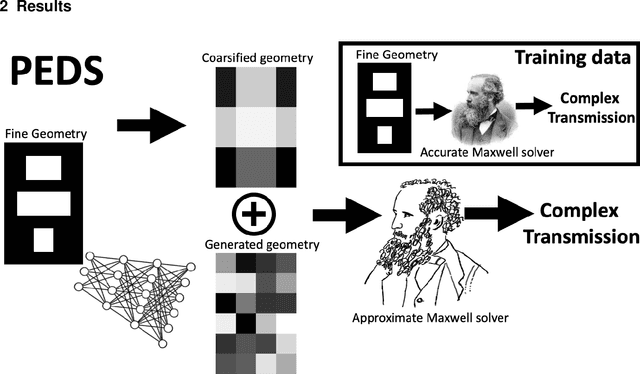
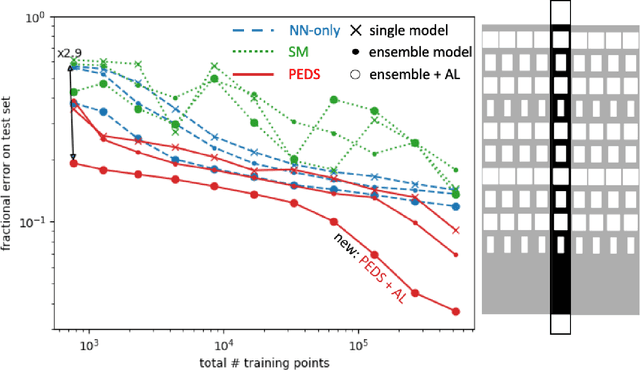
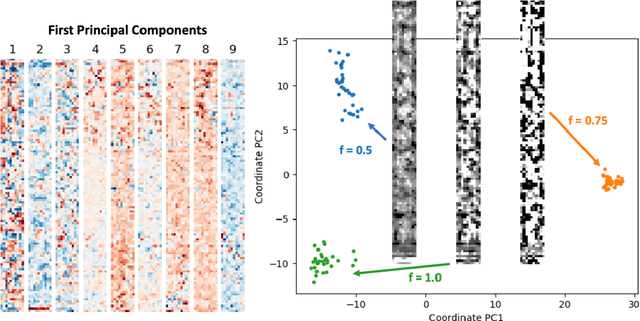
We present a "physics-enhanced deep-surrogate ("PEDS") approach towards developing fast surrogate models for complex physical systems described by partial differential equations (PDEs) and similar models: we show how to combine a low-fidelity "coarse" solver with a neural network that generates "coarsified'' inputs, trained end-to-end to globally match the output of an expensive high-fidelity numerical solver. In this way, by incorporating limited physical knowledge in the form of the low-fidelity model, we find that a PEDS surrogate can be trained with at least $\sim 10\times$ less data than a "black-box'' neural network for the same accuracy. Asymptotically, PEDS appears to learn with a steeper power law than black-box surrogates, and benefits even further when combined with active learning. We demonstrate feasibility and benefit of the proposed approach by using an example problem in electromagnetic scattering that appears in the design of optical metamaterials.

AbstractDifferentiation.jl: Backend-Agnostic Differentiable Programming in Julia

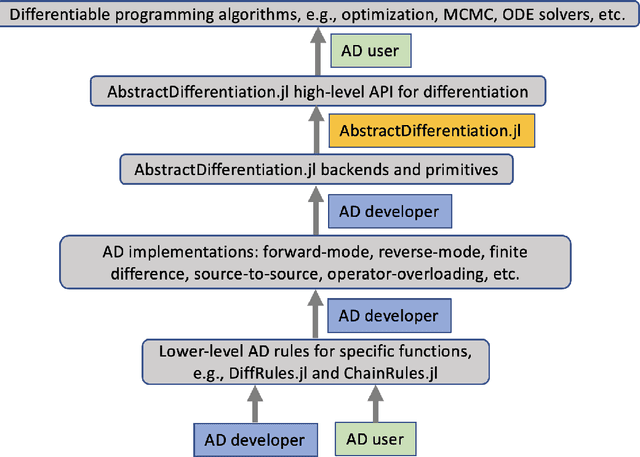
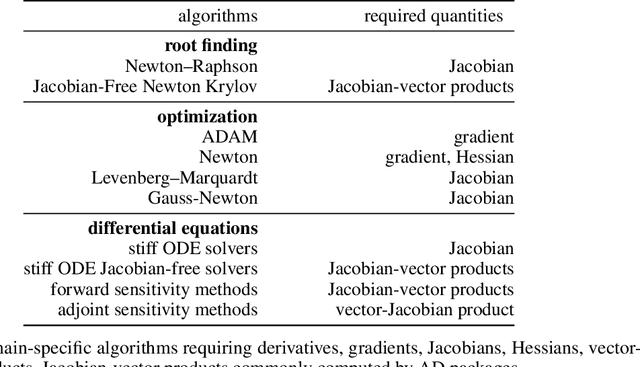
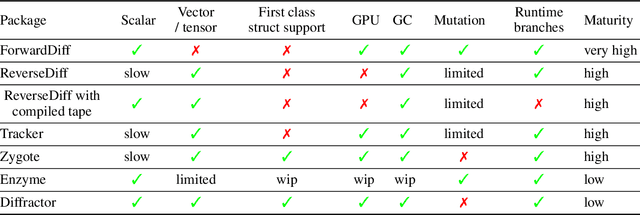
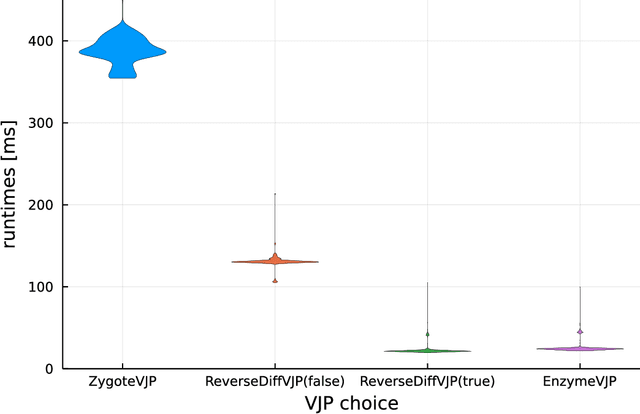
No single Automatic Differentiation (AD) system is the optimal choice for all problems. This means informed selection of an AD system and combinations can be a problem-specific variable that can greatly impact performance. In the Julia programming language, the major AD systems target the same input and thus in theory can compose. Hitherto, switching between AD packages in the Julia Language required end-users to familiarize themselves with the user-facing API of the respective packages. Furthermore, implementing a new, usable AD package required AD package developers to write boilerplate code to define convenience API functions for end-users. As a response to these issues, we present AbstractDifferentiation.jl for the automatized generation of an extensive, unified, user-facing API for any AD package. By splitting the complexity between AD users and AD developers, AD package developers only need to implement one or two primitive definitions to support various utilities for AD users like Jacobians, Hessians and lazy product operators from native primitives such as pullbacks or pushforwards, thus removing tedious -- but so far inevitable -- boilerplate code, and enabling the easy switching and composing between AD implementations for end-users.

Bayesian Neural Ordinary Differential Equations

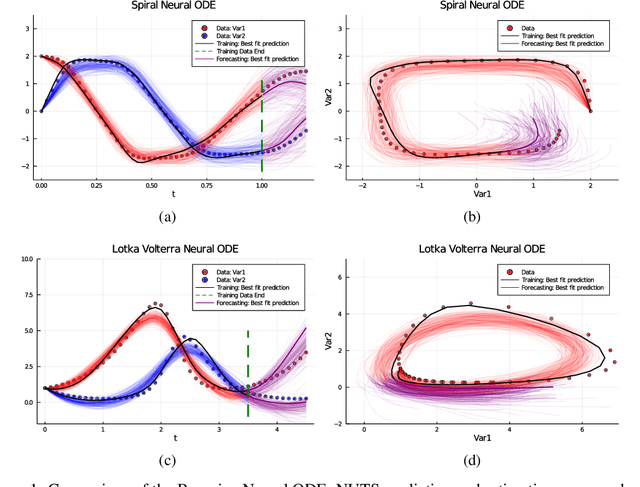
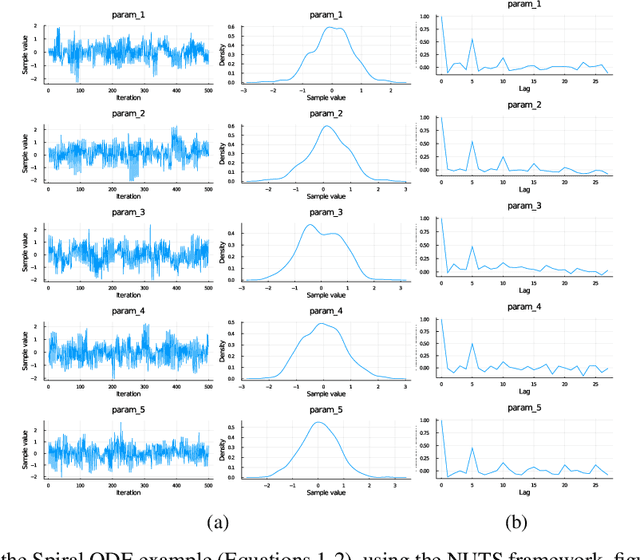
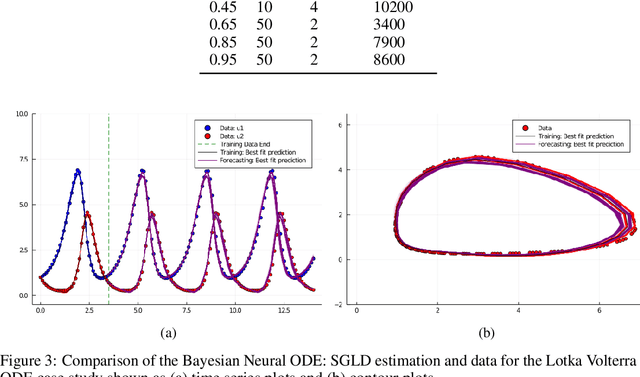
Recently, Neural Ordinary Differential Equations has emerged as a powerful framework for modeling physical simulations without explicitly defining the ODEs governing the system, but learning them via machine learning. However, the question: Can Bayesian learning frameworks be integrated with Neural ODEs to robustly quantify the uncertainty in the weights of a Neural ODE? remains unanswered. In an effort to address this question, we demonstrate the successful integration of Neural ODEs with two methods of Bayesian Inference: (a) The No-U-Turn MCMC sampler (NUTS) and (b) Stochastic Langevin Gradient Descent (SGLD). We test the performance of our Bayesian Neural ODE approach on classical physical systems, as well as on standard machine learning datasets like MNIST, using GPU acceleration. Finally, considering a simple example, we demonstrate the probabilistic identification of model specification in partially-described dynamical systems using universal ordinary differential equations. Together, this gives a scientific machine learning tool for probabilistic estimation of epistemic uncertainties.

Accelerating Simulation of Stiff Nonlinear Systems using Continuous-Time Echo State Networks

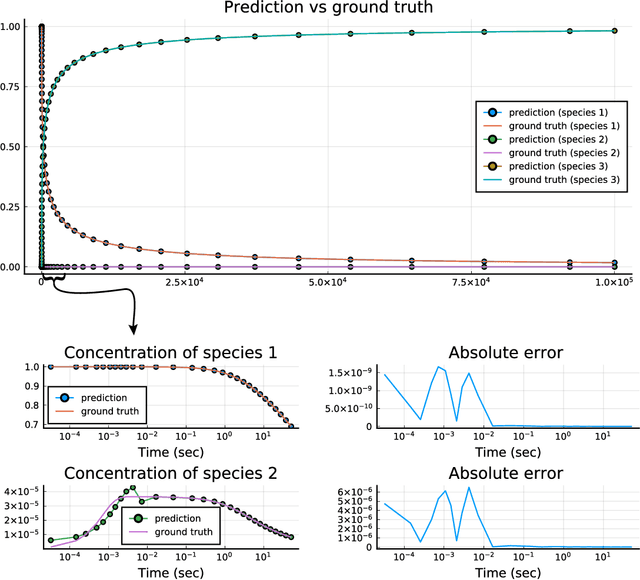
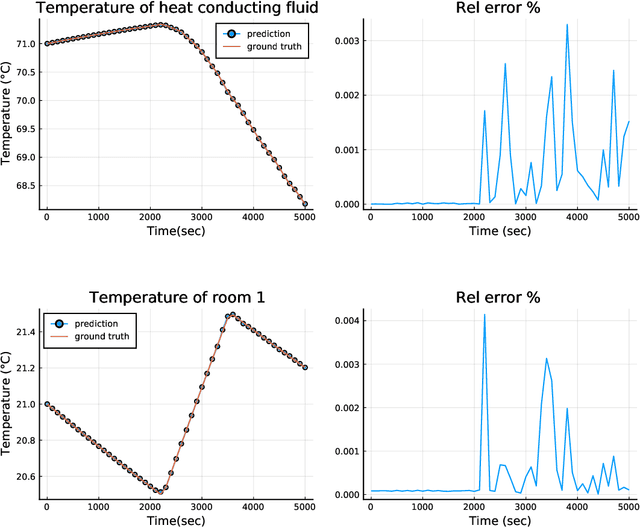
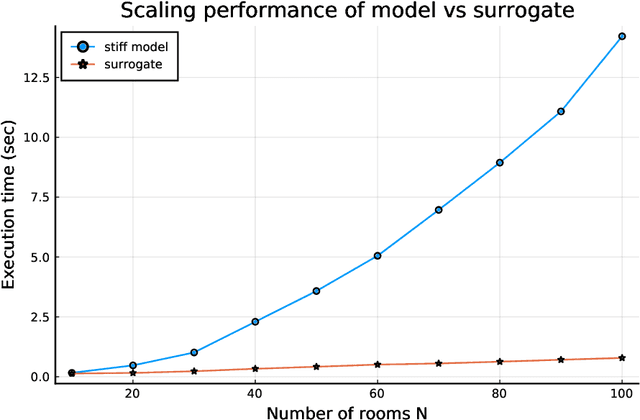
Modern design, control, and optimization often requires simulation of highly nonlinear models, leading to prohibitive computational costs. These costs can be amortized by evaluating a cheap surrogate of the full model. Here we present a general data-driven method, the continuous-time echo state network (CTESN), for generating surrogates of nonlinear ordinary differential equations with dynamics at widely separated timescales. We empirically demonstrate near-constant time performance using our CTESNs on a physically motivated scalable model of a heating system whose full execution time increases exponentially, while maintaining relative error of within 0.2 %. We also show that our model captures fast transients as well as slow dynamics effectively, while other techniques such as physics informed neural networks have difficulties trying to train and predict the highly nonlinear behavior of these models.