Forecasting N-Body Dynamics: A Comparative Study of Neural Ordinary Differential Equations and Universal Differential Equations

The n body problem, fundamental to astrophysics, simulates the motion of n bodies acting under the effect of their own mutual gravitational interactions. Traditional machine learning models that are used for predicting and forecasting trajectories are often data intensive black box models, which ignore the physical laws, thereby lacking interpretability. Whereas Scientific Machine Learning ( Scientific ML ) directly embeds the known physical laws into the machine learning framework. Through robust modelling in the Julia programming language, our method uses the Scientific ML frameworks: Neural ordinary differential equations (NODEs) and Universal differential equations (UDEs) to predict and forecast the system dynamics. In addition, an essential component of our analysis involves determining the forecasting breakdown point, which is the smallest possible amount of training data our models need to predict future, unseen data accurately. We employ synthetically created noisy data to simulate real-world observational limitations. Our findings indicate that the UDE model is much more data efficient, needing only 20% of data for a correct forecast, whereas the Neural ODE requires 90%.

Decoders Laugh as Loud as Encoders

From the dawn of the computer, Allen Turing dreamed of a robot that could communicate using language as a human being. The recent advances in the field of Large Language Models (LLMs) shocked the scientific community when a single model can apply for various natural language processing (NLP) tasks, while the output results are sometimes even better than most human communication skills. Models such as GPT, Claude, Grok, etc. have left their mark on the scientific community. However, it is unclear how much these models understand what they produce, especially in a nuanced theme such as humor. The question of whether computers understand humor is still open (among the decoders, the latest to be checked was GPT-2). We addressed this issue in this paper; we have showed that a fine-tuned decoder (GPT-4o) performed (Mean F1-macro score of 0.85) as well as the best fine-tuned encoder (RoBERTa with a Mean of F1-score 0.86)

Latent Multi-Head Attention for Small Language Models

We present the first comprehensive study of latent multi-head attention (MLA) for small language models, revealing interesting efficiency-quality trade-offs. Training 30M-parameter GPT models on 100,000 synthetic stories, we benchmark three architectural variants: standard multi-head attention (MHA), MLA, and MLA with rotary positional embeddings (MLA+RoPE). Our key finding is that MLA+RoPE with half-rank latent dimensions (r = d/2) achieves a 45% KV-cache memory reduction while incurring only a 0.3% increase in validation loss (essentially matching MHA quality)- a Pareto improvement for memory constrained deployment. We further show that RoPE is crucial for MLA in small models: without it, MLA underperforms vanilla attention by 3-5%, but with RoPE, it surpasses vanilla by 2%. Inference benchmarks on NVIDIA A100 GPUs reveal that MLA with r=d/2 achieves a 1.4 times speedup over full-rank MLA while maintaining the memory savings. GPT-4 evaluations corroborate perplexity results, with ours achieving the highest quality scores (7.4/10) across grammar, creativity, and consistency metrics. Code and models will be released upon acceptance.

NanoVLMs: How small can we go and still make coherent Vision Language Models?

Vision-Language Models (VLMs), such as GPT-4V and Llama 3.2 vision, have garnered significant research attention for their ability to leverage Large Language Models (LLMs) in multimodal tasks. However, their potential is constrained by inherent challenges, including proprietary restrictions, substantial computational demands, and limited accessibility. Smaller models, such as GIT and BLIP, exhibit marked limitations, often failing to generate coherent and consistent text beyond a few tokens, even with extensive training. This underscores a pivotal inquiry: how small can a VLM be and still produce fluent and consistent text? Drawing inspiration from the exceptional learning process of 3-4 year old children, who rely heavily on visual cues for understanding and communication, we introduce two novel datasets: ShortDesc (featuring concise image descriptions) and LongDesc (containing more detailed image descriptions). These datasets consist of image-text pairs where the text is restricted to the simple vocabulary and syntax typically used by young children, generated with a scaled- down model, GPT-4o. Using these datasets, we demonstrate that it is possible to train VLMs that are significantly smaller, up to 10 times smaller than state of the art(SOTA) small VLMs while maintaining architectural simplicity. To evaluate the outputs, we leverage GPT-4o to grade the text, as if stories written by students, on creativity, meaningfulness, and consistency, assigning scores out of 10. This method addresses limitations of standard benchmarks by accommodating unstructured outputs and providing a multidimensional evaluation of the model capabilities. Our findings contribute to the development of lightweight, accessible multimodal models for resource constrained environments.

Bayesian Neural Ordinary Differential Equations

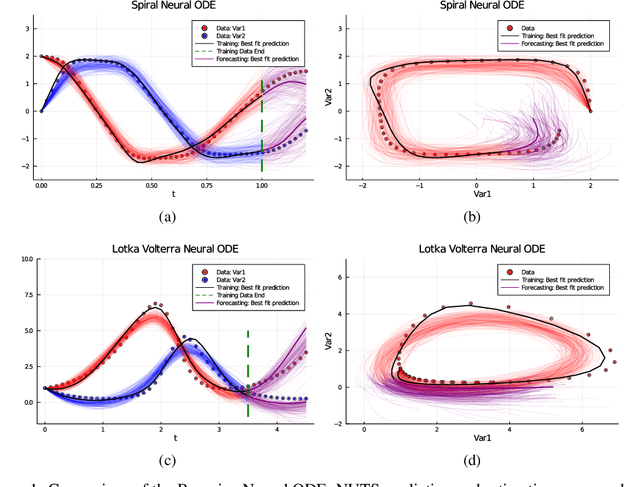
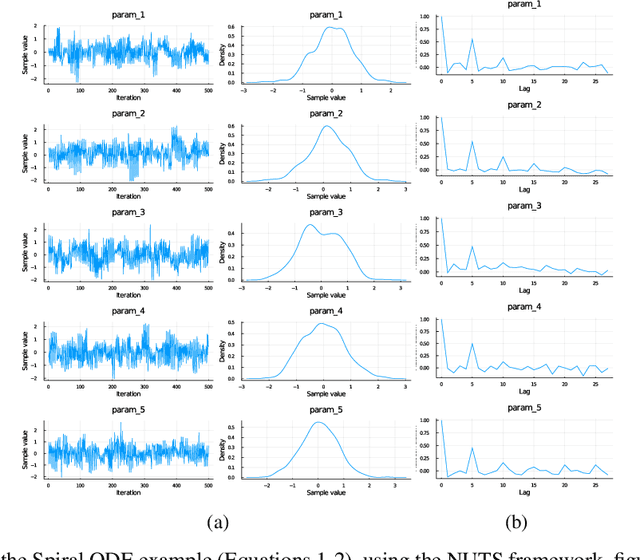
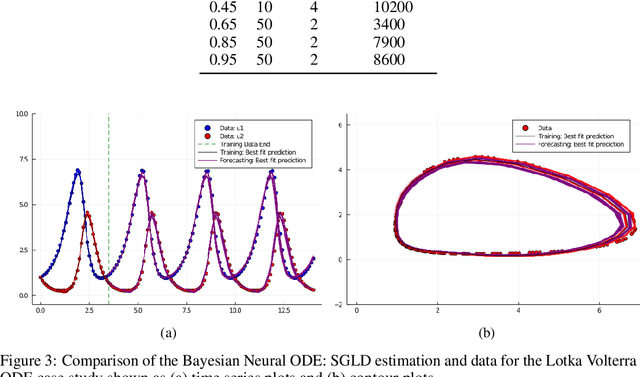
Recently, Neural Ordinary Differential Equations has emerged as a powerful framework for modeling physical simulations without explicitly defining the ODEs governing the system, but learning them via machine learning. However, the question: Can Bayesian learning frameworks be integrated with Neural ODEs to robustly quantify the uncertainty in the weights of a Neural ODE? remains unanswered. In an effort to address this question, we demonstrate the successful integration of Neural ODEs with two methods of Bayesian Inference: (a) The No-U-Turn MCMC sampler (NUTS) and (b) Stochastic Langevin Gradient Descent (SGLD). We test the performance of our Bayesian Neural ODE approach on classical physical systems, as well as on standard machine learning datasets like MNIST, using GPU acceleration. Finally, considering a simple example, we demonstrate the probabilistic identification of model specification in partially-described dynamical systems using universal ordinary differential equations. Together, this gives a scientific machine learning tool for probabilistic estimation of epistemic uncertainties.