Mohamed Tarek
Earth Movers in The Big Data Era: A Review of Optimal Transport in Machine Learning
May 08, 2023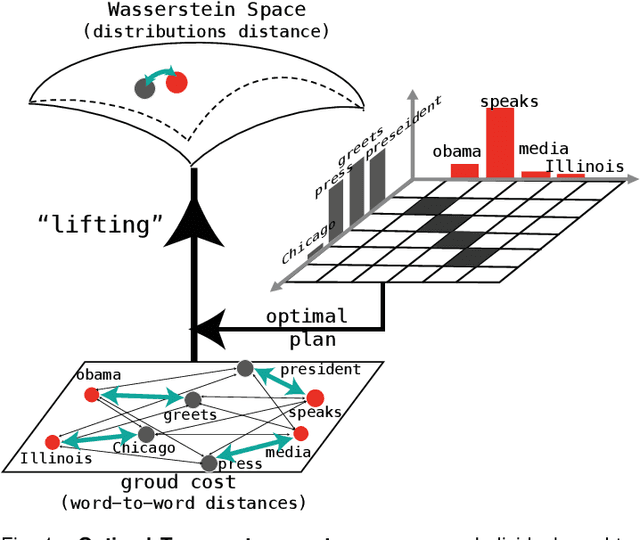
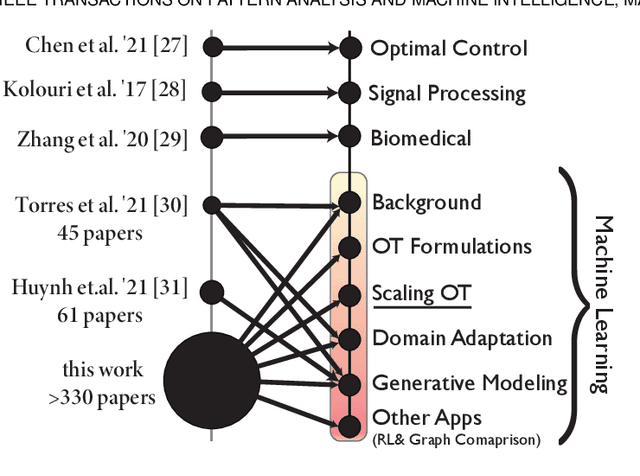
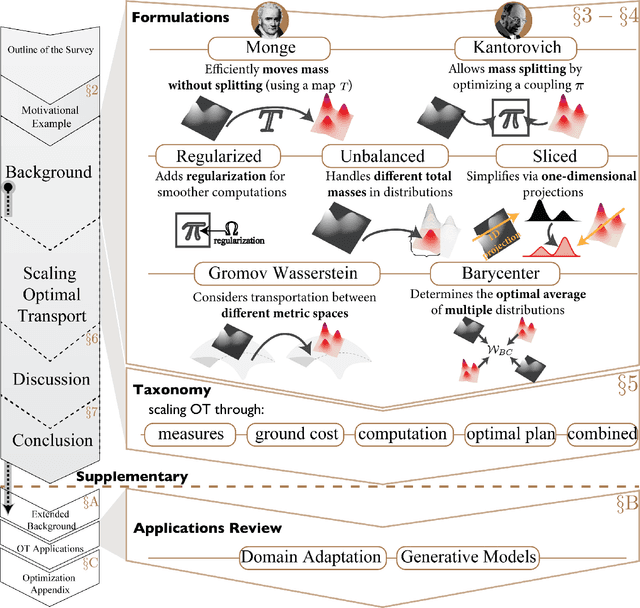
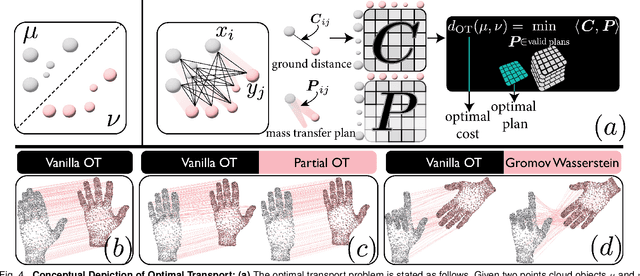
Abstract:Optimal Transport (OT) is a mathematical framework that first emerged in the eighteenth century and has led to a plethora of methods for answering many theoretical and applied questions. The last decade is a witness of the remarkable contributions of this classical optimization problem to machine learning. This paper is about where and how optimal transport is used in machine learning with a focus on the question of salable optimal transport. We provide a comprehensive survey of optimal transport while ensuring an accessible presentation as permitted by the nature of the topic and the context. First, we explain optimal transport background and introduce different flavors (i.e. mathematical formulations), properties, and notable applications. We then address the fundamental question of how to scale optimal transport to cope with the current demands of big and high dimensional data. We conduct a systematic analysis of the methods used in the literature for scaling OT and present the findings in a unified taxonomy. We conclude with presenting some open challenges and discussing potential future research directions. A live repository of related OT research papers is maintained in https://github.com/abdelwahed/OT_for_big_data.git.
A Practitioner's Guide to Bayesian Inference in Pharmacometrics using Pumas
Mar 31, 2023



Abstract:This paper provides a comprehensive tutorial for Bayesian practitioners in pharmacometrics using Pumas workflows. We start by giving a brief motivation of Bayesian inference for pharmacometrics highlighting limitations in existing software that Pumas addresses. We then follow by a description of all the steps of a standard Bayesian workflow for pharmacometrics using code snippets and examples. This includes: model definition, prior selection, sampling from the posterior, prior and posterior simulations and predictions, counter-factual simulations and predictions, convergence diagnostics, visual predictive checks, and finally model comparison with cross-validation. Finally, the background and intuition behind many advanced concepts in Bayesian statistics are explained in simple language. This includes many important ideas and precautions that users need to keep in mind when performing Bayesian analysis. Many of the algorithms, codes, and ideas presented in this paper are highly applicable to clinical research and statistical learning at large but we chose to focus our discussions on pharmacometrics in this paper to have a narrower scope in mind and given the nature of Pumas as a software primarily for pharmacometricians.
Simplifying deflation for non-convex optimization with applications in Bayesian inference and topology optimization
Jan 28, 2022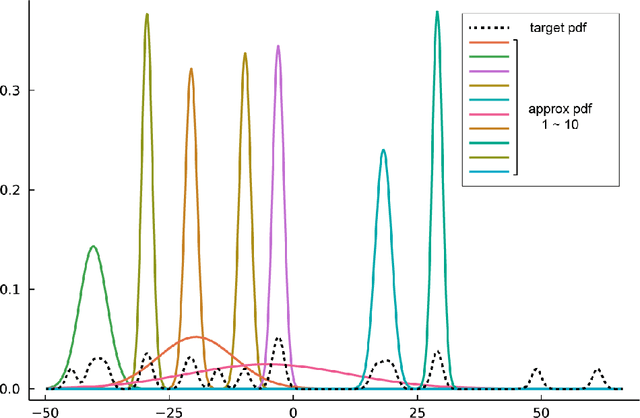
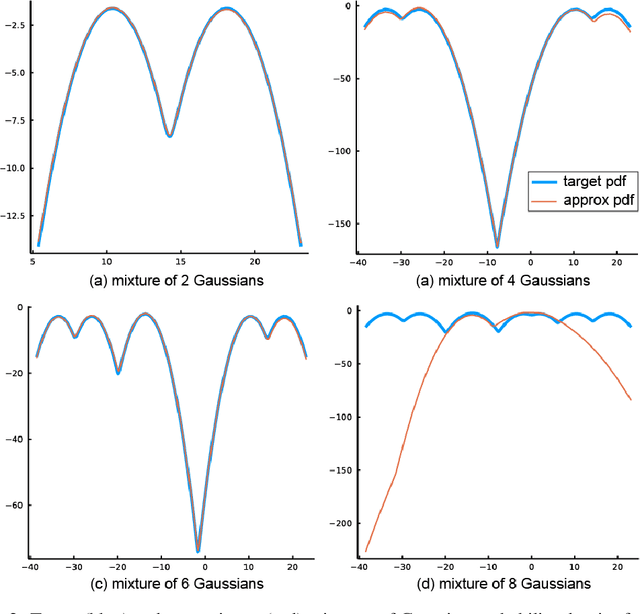

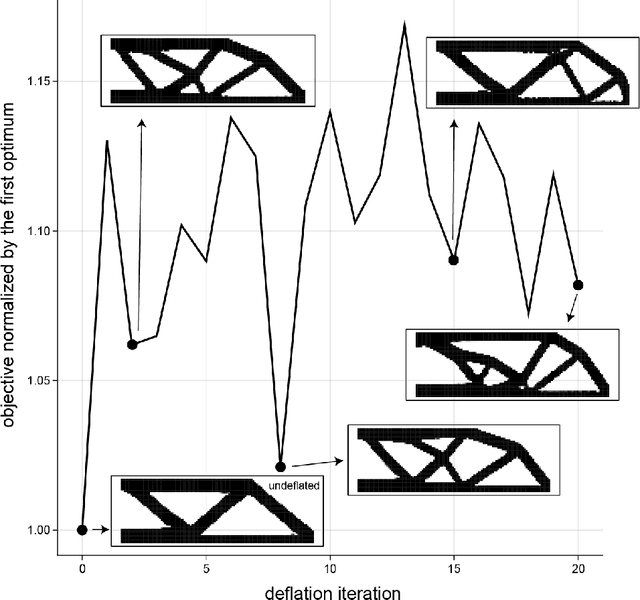
Abstract:Non-convex optimization problems have multiple local optimal solutions. Non-convex optimization problems are commonly found in numerous applications. One of the methods recently proposed to efficiently explore multiple local optimal solutions without random re-initialization relies on the concept of deflation. In this paper, different ways to use deflation in non-convex optimization and nonlinear system solving are discussed. A simple, general and novel deflation constraint is proposed to enable the use of deflation together with existing nonlinear programming solvers or nonlinear system solvers. The connection between the proposed deflation constraint and a minimum distance constraint is presented. Additionally, a number of variations of deflation constraints and their limitations are discussed. Finally, a number of applications of the proposed methodology in the fields of approximate Bayesian inference and topology optimization are presented.
AbstractDifferentiation.jl: Backend-Agnostic Differentiable Programming in Julia
Sep 25, 2021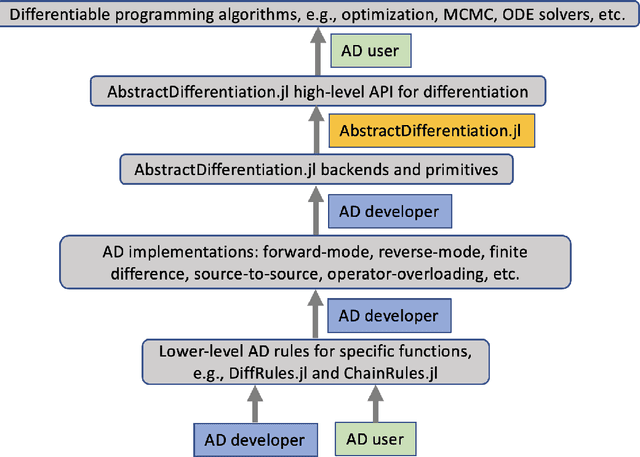
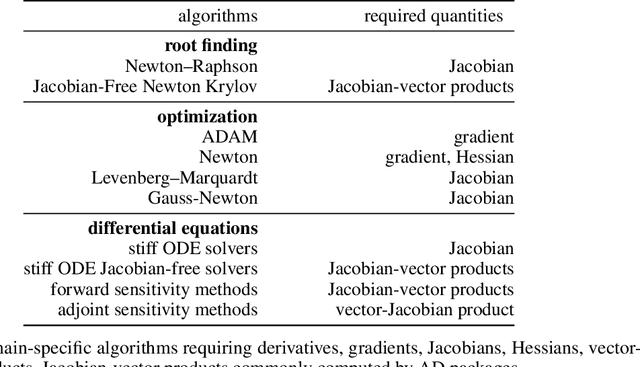
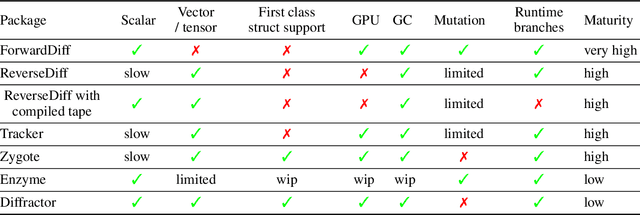
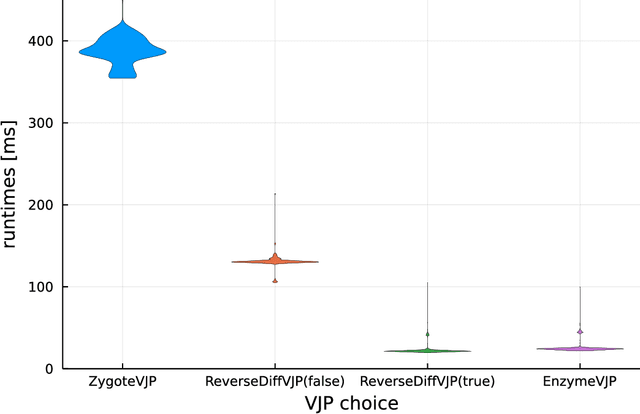
Abstract:No single Automatic Differentiation (AD) system is the optimal choice for all problems. This means informed selection of an AD system and combinations can be a problem-specific variable that can greatly impact performance. In the Julia programming language, the major AD systems target the same input and thus in theory can compose. Hitherto, switching between AD packages in the Julia Language required end-users to familiarize themselves with the user-facing API of the respective packages. Furthermore, implementing a new, usable AD package required AD package developers to write boilerplate code to define convenience API functions for end-users. As a response to these issues, we present AbstractDifferentiation.jl for the automatized generation of an extensive, unified, user-facing API for any AD package. By splitting the complexity between AD users and AD developers, AD package developers only need to implement one or two primitive definitions to support various utilities for AD users like Jacobians, Hessians and lazy product operators from native primitives such as pullbacks or pushforwards, thus removing tedious -- but so far inevitable -- boilerplate code, and enabling the easy switching and composing between AD implementations for end-users.
Bayesian Neural Ordinary Differential Equations
Dec 20, 2020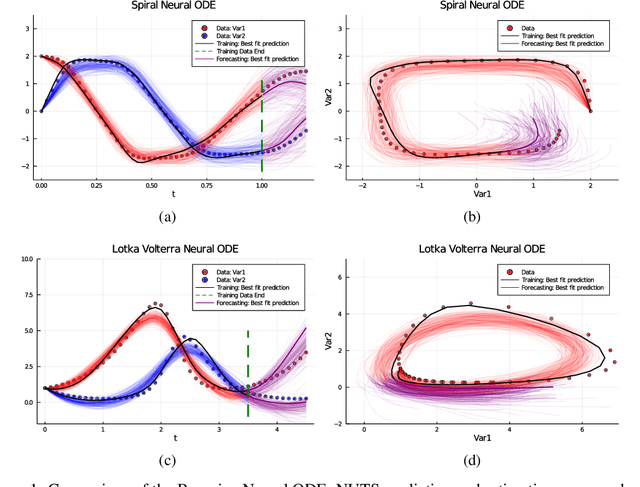
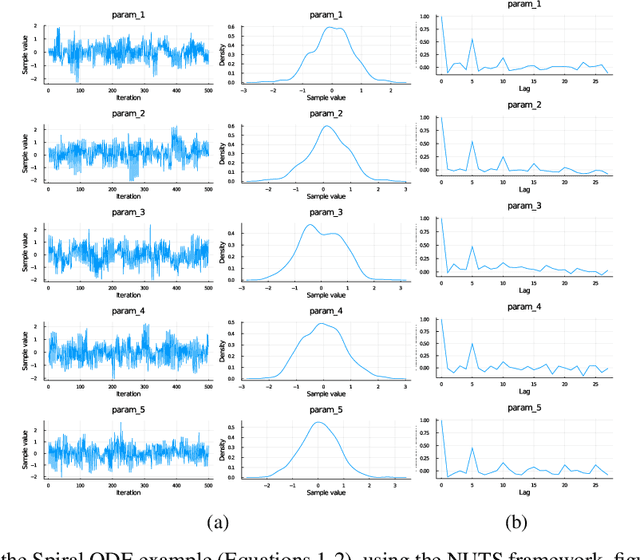

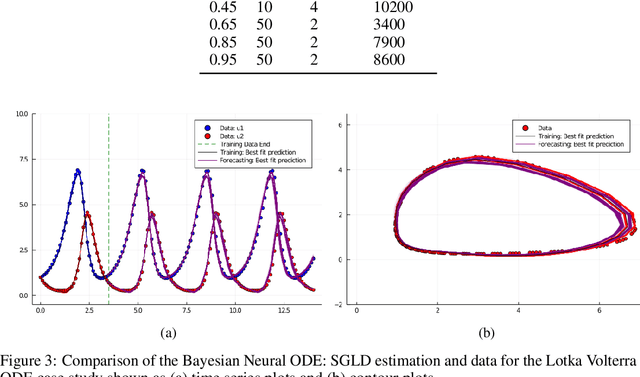
Abstract:Recently, Neural Ordinary Differential Equations has emerged as a powerful framework for modeling physical simulations without explicitly defining the ODEs governing the system, but learning them via machine learning. However, the question: Can Bayesian learning frameworks be integrated with Neural ODEs to robustly quantify the uncertainty in the weights of a Neural ODE? remains unanswered. In an effort to address this question, we demonstrate the successful integration of Neural ODEs with two methods of Bayesian Inference: (a) The No-U-Turn MCMC sampler (NUTS) and (b) Stochastic Langevin Gradient Descent (SGLD). We test the performance of our Bayesian Neural ODE approach on classical physical systems, as well as on standard machine learning datasets like MNIST, using GPU acceleration. Finally, considering a simple example, we demonstrate the probabilistic identification of model specification in partially-described dynamical systems using universal ordinary differential equations. Together, this gives a scientific machine learning tool for probabilistic estimation of epistemic uncertainties.
DynamicPPL: Stan-like Speed for Dynamic Probabilistic Models
Feb 07, 2020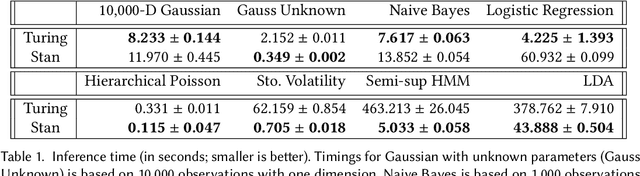
Abstract:We present the preliminary high-level design and features of DynamicPPL.jl, a modular library providing a lightning-fast infrastructure for probabilistic programming. Besides a computational performance that is often close to or better than Stan, DynamicPPL provides an intuitive DSL that allows the rapid development of complex dynamic probabilistic programs. Being entirely written in Julia, a high-level dynamic programming language for numerical computing, DynamicPPL inherits a rich set of features available through the Julia ecosystem. Since DynamicPPL is a modular, stand-alone library, any probabilistic programming system written in Julia, such as Turing.jl, can use DynamicPPL to specify models and trace their model parameters. The main features of DynamicPPL are: 1) a meta-programming based DSL for specifying dynamic models using an intuitive tilde-based notation; 2) a tracing data-structure for tracking RVs in dynamic probabilistic models; 3) a rich contextual dispatch system allowing tailored behaviour during model execution; and 4) a user-friendly syntax for probabilistic queries. Finally, we show in a variety of experiments that DynamicPPL, in combination with Turing.jl, achieves computational performance that is often close to or better than Stan.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge