Post-hoc Probabilistic Vision-Language Models

Vision-language models (VLMs), such as CLIP and SigLIP, have found remarkable success in classification, retrieval, and generative tasks. For this, VLMs deterministically map images and text descriptions to a joint latent space in which their similarity is assessed using the cosine similarity. However, a deterministic mapping of inputs fails to capture uncertainties over concepts arising from domain shifts when used in downstream tasks. In this work, we propose post-hoc uncertainty estimation in VLMs that does not require additional training. Our method leverages a Bayesian posterior approximation over the last layers in VLMs and analytically quantifies uncertainties over cosine similarities. We demonstrate its effectiveness for uncertainty quantification and support set selection in active learning. Compared to baselines, we obtain improved and well-calibrated predictive uncertainties, interpretable uncertainty estimates, and sample-efficient active learning. Our results show promise for safety-critical applications of large-scale models.

Streamlining Prediction in Bayesian Deep Learning

The rising interest in Bayesian deep learning (BDL) has led to a plethora of methods for estimating the posterior distribution. However, efficient computation of inferences, such as predictions, has been largely overlooked with Monte Carlo integration remaining the standard. In this work we examine streamlining prediction in BDL through a single forward pass without sampling. For this we use local linearisation on activation functions and local Gaussian approximations at linear layers. Thus allowing us to analytically compute an approximation to the posterior predictive distribution. We showcase our approach for both MLP and transformers, such as ViT and GPT-2, and assess its performance on regression and classification tasks.

Probabilistic Circuits for Cumulative Distribution Functions

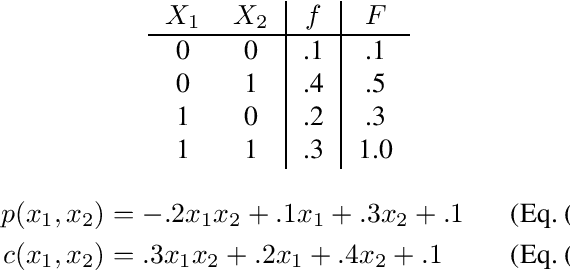
A probabilistic circuit (PC) succinctly expresses a function that represents a multivariate probability distribution and, given sufficient structural properties of the circuit, supports efficient probabilistic inference. Typically a PC computes the probability mass (or density) function (PMF or PDF) of the distribution. We consider PCs instead computing the cumulative distribution function (CDF). We show that for distributions over binary random variables these representations (PMF and CDF) are essentially equivalent, in the sense that one can be transformed to the other in polynomial time. We then show how a similar equivalence holds for distributions over finite discrete variables using a modification of the standard encoding with binary variables that aligns with the CDF semantics. Finally we show that for continuous variables, smooth, decomposable PCs computing PDFs and CDFs can be efficiently transformed to each other by modifying only the leaves of the circuit.

On Hardware-efficient Inference in Probabilistic Circuits

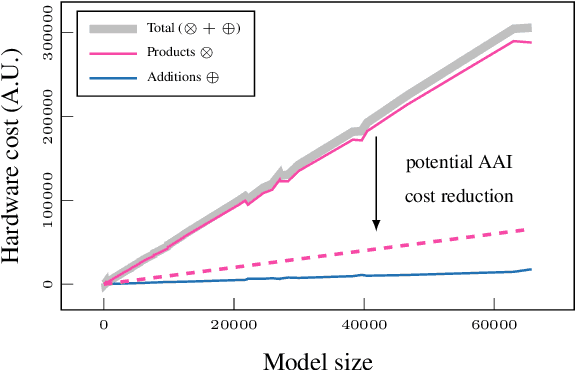
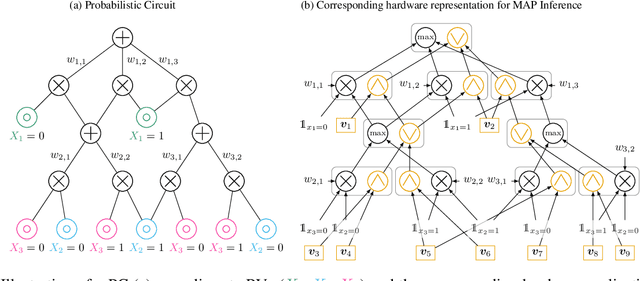
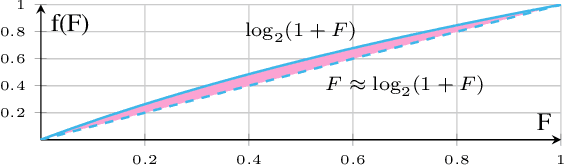
Probabilistic circuits (PCs) offer a promising avenue to perform embedded reasoning under uncertainty. They support efficient and exact computation of various probabilistic inference tasks by design. Hence, hardware-efficient computation of PCs is highly interesting for edge computing applications. As computations in PCs are based on arithmetic with probability values, they are typically performed in the log domain to avoid underflow. Unfortunately, performing the log operation on hardware is costly. Hence, prior work has focused on computations in the linear domain, resulting in high resolution and energy requirements. This work proposes the first dedicated approximate computing framework for PCs that allows for low-resolution logarithm computations. We leverage Addition As Int, resulting in linear PC computation with simple hardware elements. Further, we provide a theoretical approximation error analysis and present an error compensation mechanism. Empirically, our method obtains up to 357x and 649x energy reduction on custom hardware for evidence and MAP queries respectively with little or no computational error.

Flatness Improves Backbone Generalisation in Few-shot Classification

Deployment of deep neural networks in real-world settings typically requires adaptation to new tasks with few examples. Few-shot classification (FSC) provides a solution to this problem by leveraging pre-trained backbones for fast adaptation to new classes. Surprisingly, most efforts have only focused on developing architectures for easing the adaptation to the target domain without considering the importance of backbone training for good generalisation. We show that flatness-aware backbone training with vanilla fine-tuning results in a simpler yet competitive baseline compared to the state-of-the-art. Our results indicate that for in- and cross-domain FSC, backbone training is crucial to achieving good generalisation across different adaptation methods. We advocate more care should be taken when training these models.

Characteristic Circuits

In many real-world scenarios, it is crucial to be able to reliably and efficiently reason under uncertainty while capturing complex relationships in data. Probabilistic circuits (PCs), a prominent family of tractable probabilistic models, offer a remedy to this challenge by composing simple, tractable distributions into a high-dimensional probability distribution. However, learning PCs on heterogeneous data is challenging and densities of some parametric distributions are not available in closed form, limiting their potential use. We introduce characteristic circuits (CCs), a family of tractable probabilistic models providing a unified formalization of distributions over heterogeneous data in the spectral domain. The one-to-one relationship between characteristic functions and probability measures enables us to learn high-dimensional distributions on heterogeneous data domains and facilitates efficient probabilistic inference even when no closed-form density function is available. We show that the structure and parameters of CCs can be learned efficiently from the data and find that CCs outperform state-of-the-art density estimators for heterogeneous data domains on common benchmark data sets.

Subtractive Mixture Models via Squaring: Representation and Learning

Mixture models are traditionally represented and learned by adding several distributions as components. Allowing mixtures to subtract probability mass or density can drastically reduce the number of components needed to model complex distributions. However, learning such subtractive mixtures while ensuring they still encode a non-negative function is challenging. We investigate how to learn and perform inference on deep subtractive mixtures by squaring them. We do this in the framework of probabilistic circuits, which enable us to represent tensorized mixtures and generalize several other subtractive models. We theoretically prove that the class of squared circuits allowing subtractions can be exponentially more expressive than traditional additive mixtures; and, we empirically show this increased expressiveness on a series of real-world distribution estimation tasks.

The Robust Semantic Segmentation UNCV2023 Challenge Results

This paper outlines the winning solutions employed in addressing the MUAD uncertainty quantification challenge held at ICCV 2023. The challenge was centered around semantic segmentation in urban environments, with a particular focus on natural adversarial scenarios. The report presents the results of 19 submitted entries, with numerous techniques drawing inspiration from cutting-edge uncertainty quantification methodologies presented at prominent conferences in the fields of computer vision and machine learning and journals over the past few years. Within this document, the challenge is introduced, shedding light on its purpose and objectives, which primarily revolved around enhancing the robustness of semantic segmentation in urban scenes under varying natural adversarial conditions. The report then delves into the top-performing solutions. Moreover, the document aims to provide a comprehensive overview of the diverse solutions deployed by all participants. By doing so, it seeks to offer readers a deeper insight into the array of strategies that can be leveraged to effectively handle the inherent uncertainties associated with autonomous driving and semantic segmentation, especially within urban environments.

Fixing Overconfidence in Dynamic Neural Networks

Dynamic neural networks are a recent technique that promises a remedy for the increasing size of modern deep learning models by dynamically adapting their computational cost to the difficulty of the input samples. In this way, the model can adjust to a limited computational budget. However, the poor quality of uncertainty estimates in deep learning models makes it difficult to distinguish between hard and easy samples. To address this challenge, we present a computationally efficient approach for post-hoc uncertainty quantification in dynamic neural networks. We show that adequately quantifying and accounting for both aleatoric and epistemic uncertainty through a probabilistic treatment of the last layers improves the predictive performance and aids decision-making when determining the computational budget. In the experiments, we show improvements on CIFAR-100 and ImageNet in terms of accuracy, capturing uncertainty, and calibration error.

Transport with Support: Data-Conditional Diffusion Bridges

The dynamic Schr\"odinger bridge problem provides an appealing setting for solving optimal transport problems by learning non-linear diffusion processes using efficient iterative solvers. Recent works have demonstrated state-of-the-art results (eg. in modelling single-cell embryo RNA sequences or sampling from complex posteriors) but are limited to learning bridges with only initial and terminal constraints. Our work extends this paradigm by proposing the Iterative Smoothing Bridge (ISB). We integrate Bayesian filtering and optimal control into learning the diffusion process, enabling constrained stochastic processes governed by sparse observations at intermediate stages and terminal constraints. We assess the effectiveness of our method on synthetic and real-world data and show that the ISB generalises well to high-dimensional data, is computationally efficient, and provides accurate estimates of the marginals at intermediate and terminal times.