Fixing Overconfidence in Dynamic Neural Networks

Dynamic neural networks are a recent technique that promises a remedy for the increasing size of modern deep learning models by dynamically adapting their computational cost to the difficulty of the input samples. In this way, the model can adjust to a limited computational budget. However, the poor quality of uncertainty estimates in deep learning models makes it difficult to distinguish between hard and easy samples. To address this challenge, we present a computationally efficient approach for post-hoc uncertainty quantification in dynamic neural networks. We show that adequately quantifying and accounting for both aleatoric and epistemic uncertainty through a probabilistic treatment of the last layers improves the predictive performance and aids decision-making when determining the computational budget. In the experiments, we show improvements on CIFAR-100 and ImageNet in terms of accuracy, capturing uncertainty, and calibration error.

Periodic Activation Functions Induce Stationarity

Neural network models are known to reinforce hidden data biases, making them unreliable and difficult to interpret. We seek to build models that `know what they do not know' by introducing inductive biases in the function space. We show that periodic activation functions in Bayesian neural networks establish a connection between the prior on the network weights and translation-invariant, stationary Gaussian process priors. Furthermore, we show that this link goes beyond sinusoidal (Fourier) activations by also covering triangular wave and periodic ReLU activation functions. In a series of experiments, we show that periodic activation functions obtain comparable performance for in-domain data and capture sensitivity to perturbed inputs in deep neural networks for out-of-domain detection.

Stationary Activations for Uncertainty Calibration in Deep Learning

We introduce a new family of non-linear neural network activation functions that mimic the properties induced by the widely-used Mat\'ern family of kernels in Gaussian process (GP) models. This class spans a range of locally stationary models of various degrees of mean-square differentiability. We show an explicit link to the corresponding GP models in the case that the network consists of one infinitely wide hidden layer. In the limit of infinite smoothness the Mat\'ern family results in the RBF kernel, and in this case we recover RBF activations. Mat\'ern activation functions result in similar appealing properties to their counterparts in GP models, and we demonstrate that the local stationarity property together with limited mean-square differentiability shows both good performance and uncertainty calibration in Bayesian deep learning tasks. In particular, local stationarity helps calibrate out-of-distribution (OOD) uncertainty. We demonstrate these properties on classification and regression benchmarks and a radar emitter classification task.

Movement Tracking by Optical Flow Assisted Inertial Navigation

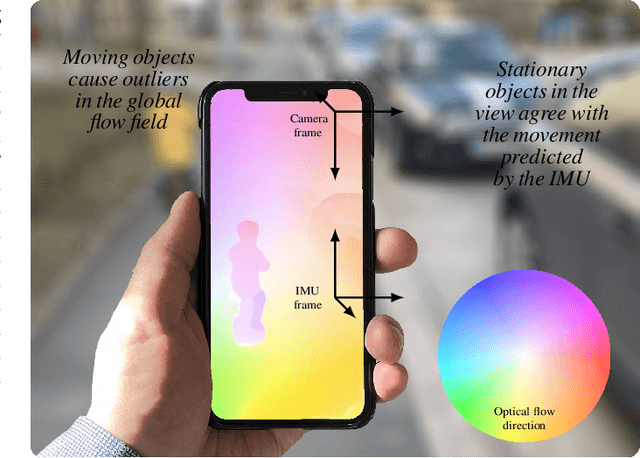
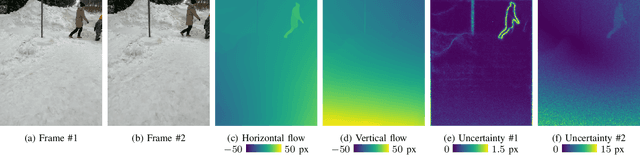
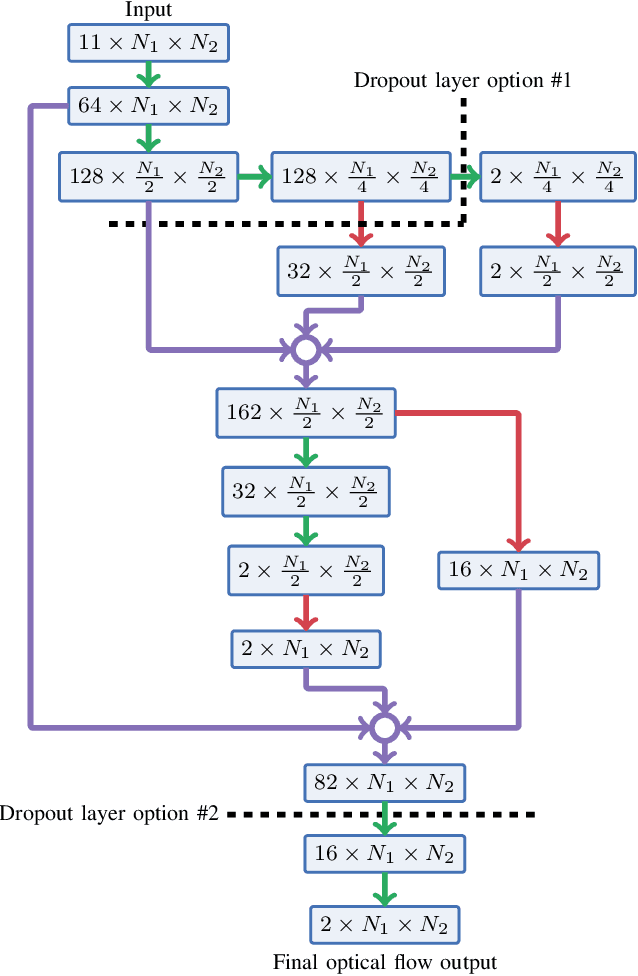
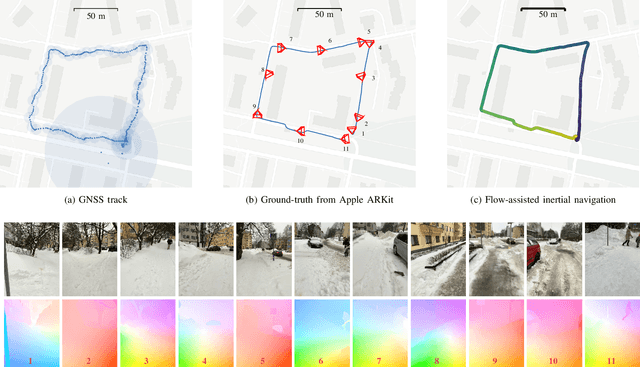
Robust and accurate six degree-of-freedom tracking on portable devices remains a challenging problem, especially on small hand-held devices such as smartphones. For improved robustness and accuracy, complementary movement information from an IMU and a camera is often fused. Conventional visual-inertial methods fuse information from IMUs with a sparse cloud of feature points tracked by the device camera. We consider a visually dense approach, where the IMU data is fused with the dense optical flow field estimated from the camera data. Learning-based methods applied to the full image frames can leverage visual cues and global consistency of the flow field to improve the flow estimates. We show how a learning-based optical flow model can be combined with conventional inertial navigation, and how ideas from probabilistic deep learning can aid the robustness of the measurement updates. The practical applicability is demonstrated on real-world data acquired by an iPad in a challenging low-texture environment.