A Compositional Atlas for Algebraic Circuits

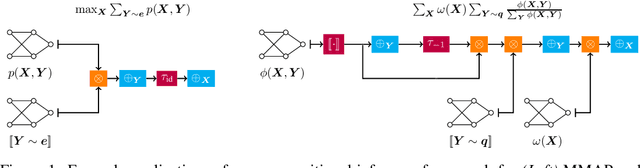
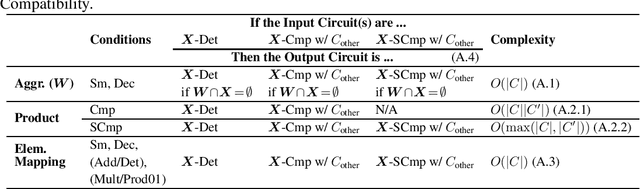
Circuits based on sum-product structure have become a ubiquitous representation to compactly encode knowledge, from Boolean functions to probability distributions. By imposing constraints on the structure of such circuits, certain inference queries become tractable, such as model counting and most probable configuration. Recent works have explored analyzing probabilistic and causal inference queries as compositions of basic operators to derive tractability conditions. In this paper, we take an algebraic perspective for compositional inference, and show that a large class of queries - including marginal MAP, probabilistic answer set programming inference, and causal backdoor adjustment - correspond to a combination of basic operators over semirings: aggregation, product, and elementwise mapping. Using this framework, we uncover simple and general sufficient conditions for tractable composition of these operators, in terms of circuit properties (e.g., marginal determinism, compatibility) and conditions on the elementwise mappings. Applying our analysis, we derive novel tractability conditions for many such compositional queries. Our results unify tractability conditions for existing problems on circuits, while providing a blueprint for analysing novel compositional inference queries.

Restructuring Tractable Probabilistic Circuits

Probabilistic circuits (PCs) is a unifying representation for probabilistic models that support tractable inference. Numerous applications of PCs like controllable text generation depend on the ability to efficiently multiply two circuits. Existing multiplication algorithms require that the circuits respect the same structure, i.e. variable scopes decomposes according to the same vtree. In this work, we propose and study the task of restructuring structured(-decomposable) PCs, that is, transforming a structured PC such that it conforms to a target vtree. We propose a generic approach for this problem and show that it leads to novel polynomial-time algorithms for multiplying circuits respecting different vtrees, as well as a practical depth-reduction algorithm that preserves structured decomposibility. Our work opens up new avenues for tractable PC inference, suggesting the possibility of training with less restrictive PC structures while enabling efficient inference by changing their structures at inference time.

PREMAP: A Unifying PREiMage APproximation Framework for Neural Networks

Most methods for neural network verification focus on bounding the image, i.e., set of outputs for a given input set. This can be used to, for example, check the robustness of neural network predictions to bounded perturbations of an input. However, verifying properties concerning the preimage, i.e., the set of inputs satisfying an output property, requires abstractions in the input space. We present a general framework for preimage abstraction that produces under- and over-approximations of any polyhedral output set. Our framework employs cheap parameterised linear relaxations of the neural network, together with an anytime refinement procedure that iteratively partitions the input region by splitting on input features and neurons. The effectiveness of our approach relies on carefully designed heuristics and optimization objectives to achieve rapid improvements in the approximation volume. We evaluate our method on a range of tasks, demonstrating significant improvement in efficiency and scalability to high-input-dimensional image classification tasks compared to state-of-the-art techniques. Further, we showcase the application to quantitative verification and robustness analysis, presenting a sound and complete algorithm for the former and providing sound quantitative results for the latter.

Where is the signal in tokenization space?

Large Language Models (LLMs) are typically shipped with tokenizers that deterministically encode text into so-called canonical token sequences, to which the LLMs assign probability values. One common assumption is that the probability of a piece of text is the probability of its canonical token sequence. However, the tokenization of a string is not unique: e.g., the Llama2 tokenizer encodes Tokens as [Tok,ens], but [Tok,en,s] also represents the same text. In this paper, we study non-canonical tokenizations. We prove that, given a string, it is computationally hard to find the most likely tokenization for an autoregressive LLM, as well as to compute the marginal probability over all possible tokenizations. We then show how the marginal is, in most cases, indistinguishable from the canonical probability. Surprisingly, we then empirically demonstrate the existence of a significant amount of signal hidden within tokenization space. Notably, by simply aggregating the probabilities of non-canonical tokenizations, we achieve improvements across a range of LLM evaluation benchmarks for a variety of architectures, including transformers and state space models.

Probabilistic Circuits for Cumulative Distribution Functions

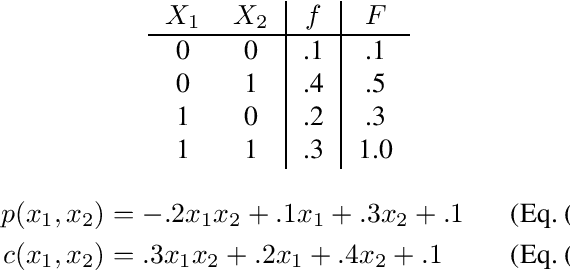
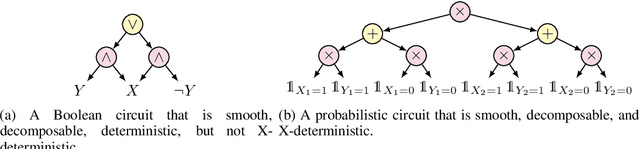
A probabilistic circuit (PC) succinctly expresses a function that represents a multivariate probability distribution and, given sufficient structural properties of the circuit, supports efficient probabilistic inference. Typically a PC computes the probability mass (or density) function (PMF or PDF) of the distribution. We consider PCs instead computing the cumulative distribution function (CDF). We show that for distributions over binary random variables these representations (PMF and CDF) are essentially equivalent, in the sense that one can be transformed to the other in polynomial time. We then show how a similar equivalence holds for distributions over finite discrete variables using a modification of the standard encoding with binary variables that aligns with the CDF semantics. Finally we show that for continuous variables, smooth, decomposable PCs computing PDFs and CDFs can be efficiently transformed to each other by modifying only the leaves of the circuit.

On the Relationship Between Monotone and Squared Probabilistic Circuits

Probabilistic circuits are a unifying representation of functions as computation graphs of weighted sums and products. Their primary application is in probabilistic modeling, where circuits with non-negative weights (monotone circuits) can be used to represent and learn density/mass functions, with tractable marginal inference. Recently, it was proposed to instead represent densities as the square of the circuit function (squared circuits); this allows the use of negative weights while retaining tractability, and can be exponentially more compact than monotone circuits. Unfortunately, we show the reverse also holds, meaning that monotone circuits and squared circuits are incomparable in general. This raises the question of whether we can reconcile, and indeed improve upon the two modeling approaches. We answer in the positive by proposing InceptionPCs, a novel type of circuit that naturally encompasses both monotone circuits and squared circuits as special cases, and employs complex parameters. Empirically, we validate that InceptionPCs can outperform both monotone and squared circuits on image datasets.

Neural Structure Learning with Stochastic Differential Equations

Discovering the underlying relationships among variables from temporal observations has been a longstanding challenge in numerous scientific disciplines, including biology, finance, and climate science. The dynamics of such systems are often best described using continuous-time stochastic processes. Unfortunately, most existing structure learning approaches assume that the underlying process evolves in discrete-time and/or observations occur at regular time intervals. These mismatched assumptions can often lead to incorrect learned structures and models. In this work, we introduce a novel structure learning method, SCOTCH, which combines neural stochastic differential equations (SDE) with variational inference to infer a posterior distribution over possible structures. This continuous-time approach can naturally handle both learning from and predicting observations at arbitrary time points. Theoretically, we establish sufficient conditions for an SDE and SCOTCH to be structurally identifiable, and prove its consistency under infinite data limits. Empirically, we demonstrate that our approach leads to improved structure learning performance on both synthetic and real-world datasets compared to relevant baselines under regular and irregular sampling intervals.

On Preimage Approximation for Neural Networks

Neural network verification mainly focuses on local robustness properties. However, often it is important to know whether a given property holds globally for the whole input domain, and if not then for what proportion of the input the property is true. While exact preimage generation can construct an equivalent representation of neural networks that can aid such (quantitative) global robustness verification, it is intractable at scale. In this work, we propose an efficient and practical anytime algorithm for generating symbolic under-approximations of the preimage of neural networks based on linear relaxation. Our algorithm iteratively minimizes the volume approximation error by partitioning the input region into subregions, where the neural network relaxation bounds become tighter. We further employ sampling and differentiable approximations to the volume in order to prioritize regions to split and optimize the parameters of the relaxation, leading to faster improvement and more compact under-approximations. Evaluation results demonstrate that our approach is able to generate preimage approximations significantly faster than exact methods and scales to neural network controllers for which exact preimage generation is intractable. We also demonstrate an application of our approach to quantitative global verification.

Compositional Probabilistic and Causal Inference using Tractable Circuit Models

Probabilistic circuits (PCs) are a class of tractable probabilistic models, which admit efficient inference routines depending on their structural properties. In this paper, we introduce md-vtrees, a novel structural formulation of (marginal) determinism in structured decomposable PCs, which generalizes previously proposed classes such as probabilistic sentential decision diagrams. Crucially, we show how mdvtrees can be used to derive tractability conditions and efficient algorithms for advanced inference queries expressed as arbitrary compositions of basic probabilistic operations, such as marginalization, multiplication and reciprocals, in a sound and generalizable manner. In particular, we derive the first polytime algorithms for causal inference queries such as backdoor adjustment on PCs. As a practical instantiation of the framework, we propose MDNets, a novel PC architecture using md-vtrees, and empirically demonstrate their application to causal inference.

Bayesian Network Models of Causal Interventions in Healthcare Decision Making: Literature Review and Software Evaluation

This report summarises the outcomes of a systematic literature search to identify Bayesian network models used to support decision making in healthcare. After describing the search methodology, the selected research papers are briefly reviewed, with the view to identify publicly available models and datasets that are well suited to analysis using the causal interventional analysis software tool developed in Wang B, Lyle C, Kwiatkowska M (2021). Finally, an experimental evaluation of applying the software on a selection of models is carried out and preliminary results are reported.