Discovering and Learning Probabilistic Models of Black-Box AI Capabilities

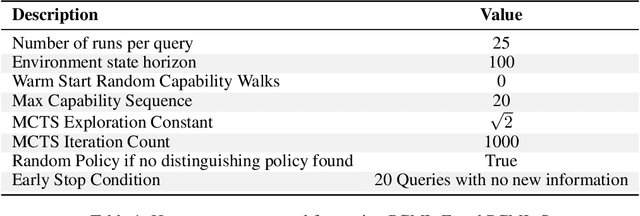
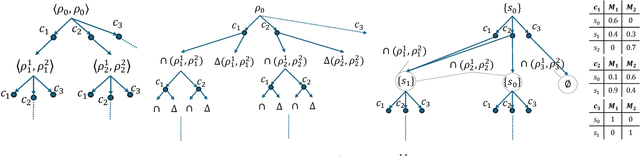
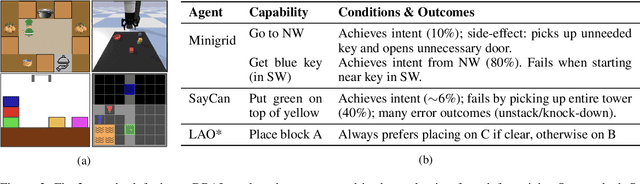
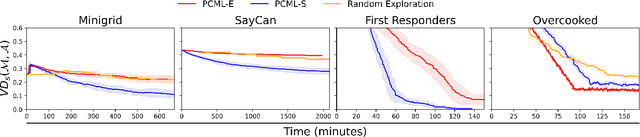
Black-box AI (BBAI) systems such as foundational models are increasingly being used for sequential decision making. To ensure that such systems are safe to operate and deploy, it is imperative to develop efficient methods that can provide a sound and interpretable representation of the BBAI's capabilities. This paper shows that PDDL-style representations can be used to efficiently learn and model an input BBAI's planning capabilities. It uses the Monte-Carlo tree search paradigm to systematically create test tasks, acquire data, and prune the hypothesis space of possible symbolic models. Learned models describe a BBAI's capabilities, the conditions under which they can be executed, and the possible outcomes of executing them along with their associated probabilities. Theoretical results show soundness, completeness and convergence of the learned models. Empirical results with multiple BBAI systems illustrate the scope, efficiency, and accuracy of the presented methods.

A Compositional Atlas for Algebraic Circuits

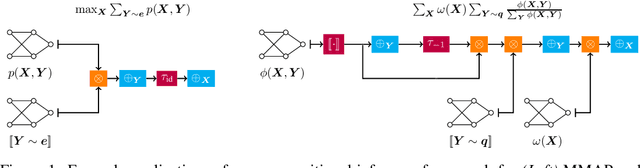
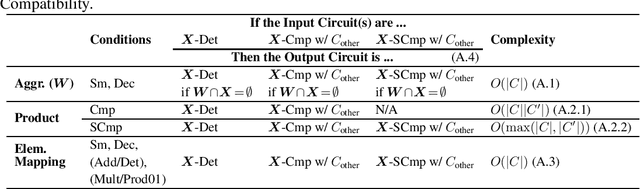
Circuits based on sum-product structure have become a ubiquitous representation to compactly encode knowledge, from Boolean functions to probability distributions. By imposing constraints on the structure of such circuits, certain inference queries become tractable, such as model counting and most probable configuration. Recent works have explored analyzing probabilistic and causal inference queries as compositions of basic operators to derive tractability conditions. In this paper, we take an algebraic perspective for compositional inference, and show that a large class of queries - including marginal MAP, probabilistic answer set programming inference, and causal backdoor adjustment - correspond to a combination of basic operators over semirings: aggregation, product, and elementwise mapping. Using this framework, we uncover simple and general sufficient conditions for tractable composition of these operators, in terms of circuit properties (e.g., marginal determinism, compatibility) and conditions on the elementwise mappings. Applying our analysis, we derive novel tractability conditions for many such compositional queries. Our results unify tractability conditions for existing problems on circuits, while providing a blueprint for analysing novel compositional inference queries.

Optimal Transport for Probabilistic Circuits

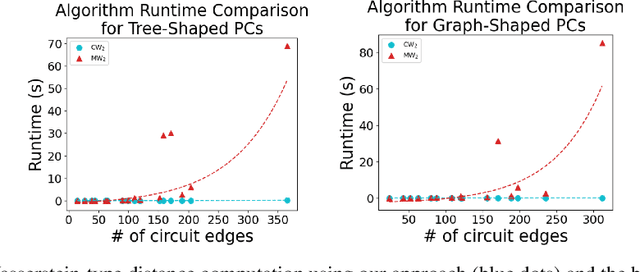
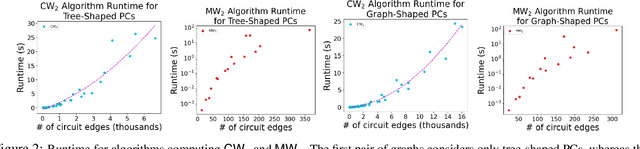
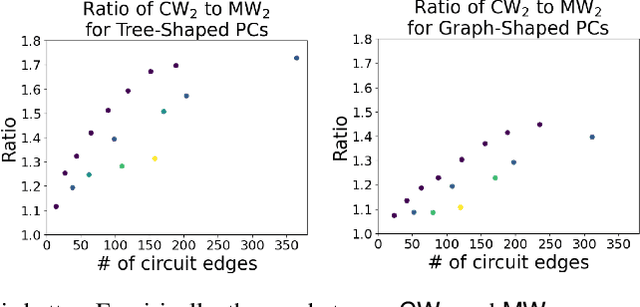
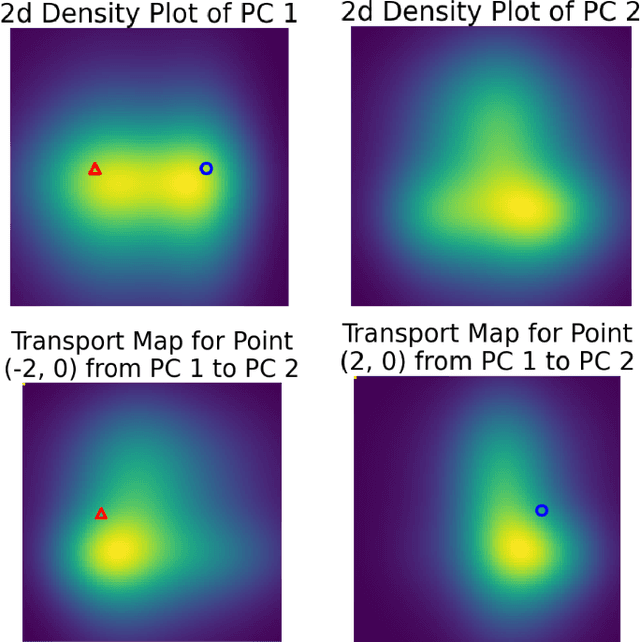
We introduce a novel optimal transport framework for probabilistic circuits (PCs). While it has been shown recently that divergences between distributions represented as certain classes of PCs can be computed tractably, to the best of our knowledge, there is no existing approach to compute the Wasserstein distance between probability distributions given by PCs. We consider a Wasserstein-type distance that restricts the coupling measure of the associated optimal transport problem to be a probabilistic circuit. We then develop an algorithm for computing this distance by solving a series of small linear programs and derive the circuit conditions under which this is tractable. Furthermore, we show that we can also retrieve the optimal transport plan between the PCs from the solutions to these linear programming problems. We then consider the empirical Wasserstein distance between a PC and a dataset, and show that we can estimate the PC parameters to minimize this distance through an efficient iterative algorithm.

Certifying Fairness of Probabilistic Circuits

With the increased use of machine learning systems for decision making, questions about the fairness properties of such systems start to take center stage. Most existing work on algorithmic fairness assume complete observation of features at prediction time, as is the case for popular notions like statistical parity and equal opportunity. However, this is not sufficient for models that can make predictions with partial observation as we could miss patterns of bias and incorrectly certify a model to be fair. To address this, a recently introduced notion of fairness asks whether the model exhibits any discrimination pattern, in which an individual characterized by (partial) feature observations, receives vastly different decisions merely by disclosing one or more sensitive attributes such as gender and race. By explicitly accounting for partial observations, this provides a much more fine-grained notion of fairness. In this paper, we propose an algorithm to search for discrimination patterns in a general class of probabilistic models, namely probabilistic circuits. Previously, such algorithms were limited to naive Bayes classifiers which make strong independence assumptions; by contrast, probabilistic circuits provide a unifying framework for a wide range of tractable probabilistic models and can even be compiled from certain classes of Bayesian networks and probabilistic programs, making our method much more broadly applicable. Furthermore, for an unfair model, it may be useful to quickly find discrimination patterns and distill them for better interpretability. As such, we also propose a sampling-based approach to more efficiently mine discrimination patterns, and introduce new classes of patterns such as minimal, maximal, and Pareto optimal patterns that can effectively summarize exponentially many discrimination patterns

Solving Marginal MAP Exactly by Probabilistic Circuit Transformations

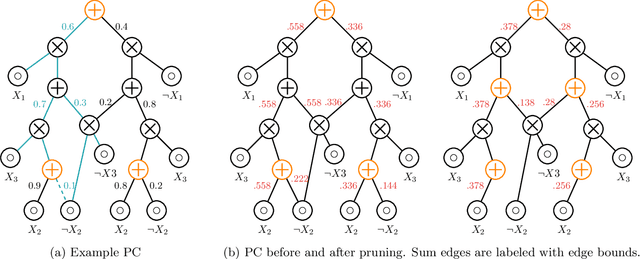
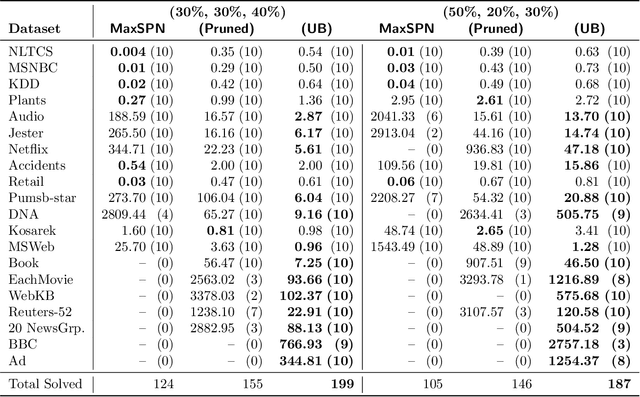
Probabilistic circuits (PCs) are a class of tractable probabilistic models that allow efficient, often linear-time, inference of queries such as marginals and most probable explanations (MPE). However, marginal MAP, which is central to many decision-making problems, remains a hard query for PCs unless they satisfy highly restrictive structural constraints. In this paper, we develop a pruning algorithm that removes parts of the PC that are irrelevant to a marginal MAP query, shrinking the PC while maintaining the correct solution. This pruning technique is so effective that we are able to build a marginal MAP solver based solely on iteratively transforming the circuit -- no search is required. We empirically demonstrate the efficacy of our approach on real-world datasets.

A Compositional Atlas of Tractable Circuit Operations: From Simple Transformations to Complex Information-Theoretic Queries

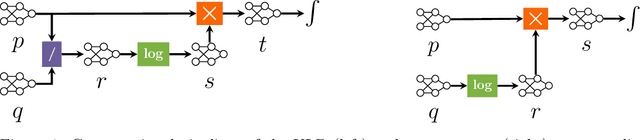
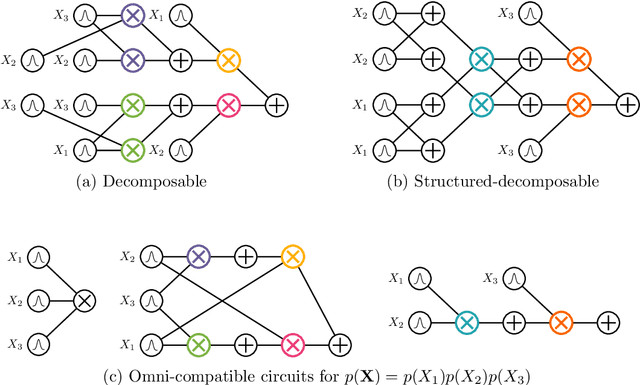
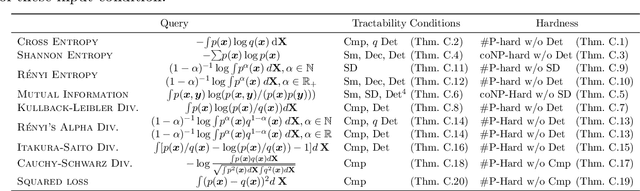
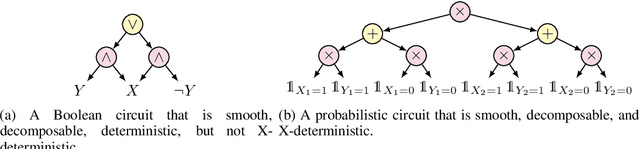
Circuit representations are becoming the lingua franca to express and reason about tractable generative and discriminative models. In this paper, we show how complex inference scenarios for these models that commonly arise in machine learning -- from computing the expectations of decision tree ensembles to information-theoretic divergences of deep mixture models -- can be represented in terms of tractable modular operations over circuits. Specifically, we characterize the tractability of a vocabulary of simple transformations -- sums, products, quotients, powers, logarithms, and exponentials -- in terms of sufficient structural constraints of the circuits they operate on, and present novel hardness results for the cases in which these properties are not satisfied. Building on these operations, we derive a unified framework for reasoning about tractable models that generalizes several results in the literature and opens up novel tractable inference scenarios.

Group Fairness by Probabilistic Modeling with Latent Fair Decisions

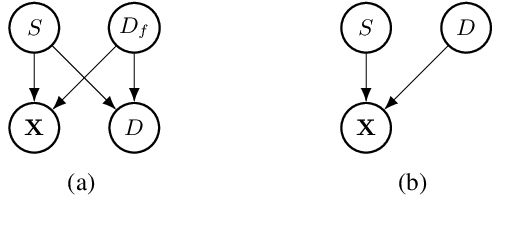
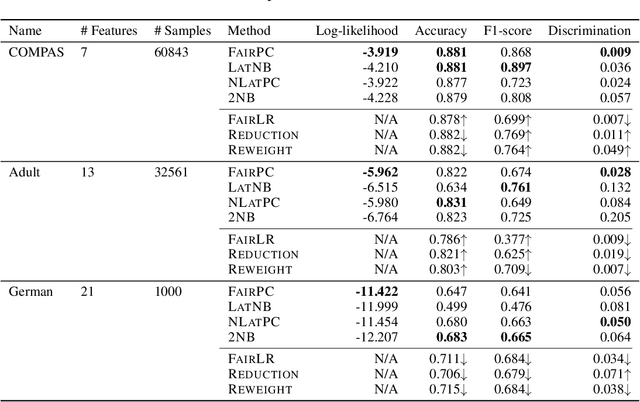
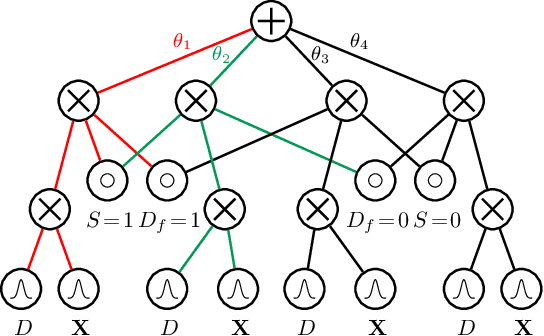
Machine learning systems are increasingly being used to make impactful decisions such as loan applications and criminal justice risk assessments, and as such, ensuring fairness of these systems is critical. This is often challenging as the labels in the data are biased. This paper studies learning fair probability distributions from biased data by explicitly modeling a latent variable that represents a hidden, unbiased label. In particular, we aim to achieve demographic parity by enforcing certain independencies in the learned model. We also show that group fairness guarantees are meaningful only if the distribution used to provide those guarantees indeed captures the real-world data. In order to closely model the data distribution, we employ probabilistic circuits, an expressive and tractable probabilistic model, and propose an algorithm to learn them from incomplete data. We evaluate our approach on a synthetic dataset in which observed labels indeed come from fair labels but with added bias, and demonstrate that the fair labels are successfully retrieved. Moreover, we show on real-world datasets that our approach not only is a better model than existing methods of how the data was generated but also achieves competitive accuracy.

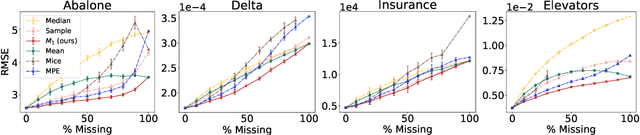
Handling Missing Data in Decision Trees: A Probabilistic Approach

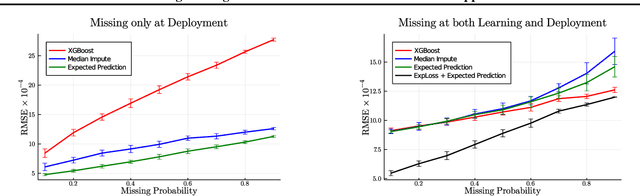
Decision trees are a popular family of models due to their attractive properties such as interpretability and ability to handle heterogeneous data. Concurrently, missing data is a prevalent occurrence that hinders performance of machine learning models. As such, handling missing data in decision trees is a well studied problem. In this paper, we tackle this problem by taking a probabilistic approach. At deployment time, we use tractable density estimators to compute the "expected prediction" of our models. At learning time, we fine-tune parameters of already learned trees by minimizing their "expected prediction loss" w.r.t.\ our density estimators. We provide brief experiments showcasing effectiveness of our methods compared to few baselines.

On Tractable Computation of Expected Predictions

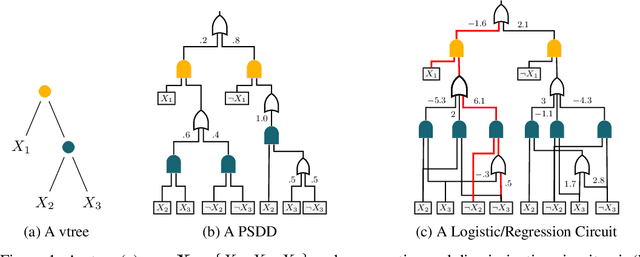
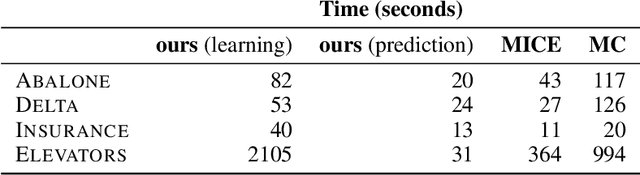
Computing expected predictions of discriminative models is a fundamental task in machine learning that appears in many interesting applications such as fairness, handling missing values, and data analysis. Unfortunately, computing expectations of a discriminative model with respect to a probability distribution defined by an arbitrary generative model has been proven to be hard in general. In fact, the task is intractable even for simple models such as logistic regression and a naive Bayes distribution. In this paper, we identify a pair of generative and discriminative models that enables tractable computation of expectations, as well as moments of any order, of the latter with respect to the former in case of regression. Specifically, we consider expressive probabilistic circuits with certain structural constraints that support tractable probabilistic inference. Moreover, we exploit the tractable computation of high-order moments to derive an algorithm to approximate the expectations for classification scenarios in which exact computations are intractable. Our framework to compute expected predictions allows for handling of missing data during prediction time in a principled and accurate way and enables reasoning about the behavior of discriminative models. We empirically show our algorithm to consistently outperform standard imputation techniques on a variety of datasets. Finally, we illustrate how our framework can be used for exploratory data analysis.

Learning Fair Naive Bayes Classifiers by Discovering and Eliminating Discrimination Patterns

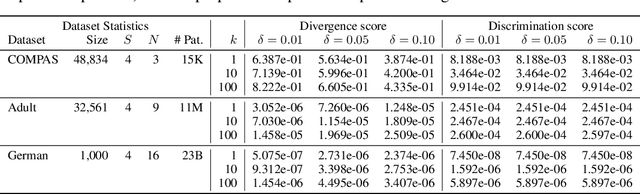
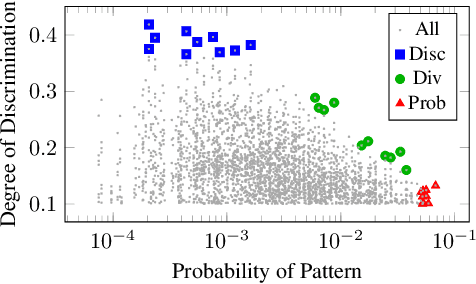
As machine learning is increasingly used to make real-world decisions, recent research efforts aim to define and ensure fairness in algorithmic decision making. Existing methods often assume a fixed set of observable features to define individuals, but lack a discussion of certain features not being observed at test time. In this paper, we study fairness of naive Bayes classifiers, which allow partial observations. In particular, we introduce the notion of a discrimination pattern, which refers to an individual receiving different classifications depending on whether some sensitive attributes were observed. Then a model is considered fair if it has no such pattern. We propose an algorithm to discover and mine for discrimination patterns in a naive Bayes classifier, and show how to learn maximum-likelihood parameters subject to these fairness constraints. Our approach iteratively discovers and eliminates discrimination patterns until a fair model is learned. An empirical evaluation on three real-world datasets demonstrates that we can remove exponentially many discrimination patterns by only adding a small fraction of them as constraints.