Mechanistic evaluation of Transformers and state space models

State space models (SSMs) for language modelling promise an efficient and performant alternative to quadratic-attention Transformers, yet show variable performance on recalling basic information from the context. While performance on synthetic tasks like Associative Recall (AR) can point to this deficiency, behavioural metrics provide little information as to why--on a mechanistic level--certain architectures fail and others succeed. To address this, we conduct experiments on AR and find that only Transformers and Based SSM models fully succeed at AR, with Mamba a close third, whereas the other SSMs (H3, Hyena) fail. We then use causal interventions to explain why. We find that Transformers and Based learn to store key-value associations in-context using induction heads. By contrast, the SSMs compute these associations only at the last state, with only Mamba succeeding because of its short convolution component. To extend and deepen these findings, we introduce Associative Treecall (ATR), a synthetic task similar to AR based on PCFG induction. ATR introduces language-like hierarchical structure into the AR setting. We find that all architectures learn the same mechanism as they did for AR, and the same three models succeed at the task. These results reveal that architectures with similar accuracy may still have substantive differences, motivating the adoption of mechanistic evaluations.

Self-Refining Diffusion Samplers: Enabling Parallelization via Parareal Iterations

In diffusion models, samples are generated through an iterative refinement process, requiring hundreds of sequential model evaluations. Several recent methods have introduced approximations (fewer discretization steps or distillation) to trade off speed at the cost of sample quality. In contrast, we introduce Self-Refining Diffusion Samplers (SRDS) that retain sample quality and can improve latency at the cost of additional parallel compute. We take inspiration from the Parareal algorithm, a popular numerical method for parallel-in-time integration of differential equations. In SRDS, a quick but rough estimate of a sample is first created and then iteratively refined in parallel through Parareal iterations. SRDS is not only guaranteed to accurately solve the ODE and converge to the serial solution but also benefits from parallelization across the diffusion trajectory, enabling batched inference and pipelining. As we demonstrate for pre-trained diffusion models, the early convergence of this refinement procedure drastically reduces the number of steps required to produce a sample, speeding up generation for instance by up to 1.7x on a 25-step StableDiffusion-v2 benchmark and up to 4.3x on longer trajectories.

Mixtures of All Trees

Tree-shaped graphical models are widely used for their tractability. However, they unfortunately lack expressive power as they require committing to a particular sparse dependency structure. We propose a novel class of generative models called mixtures of all trees: that is, a mixture over all possible ($n^{n-2}$) tree-shaped graphical models over $n$ variables. We show that it is possible to parameterize this Mixture of All Trees (MoAT) model compactly (using a polynomial-size representation) in a way that allows for tractable likelihood computation and optimization via stochastic gradient descent. Furthermore, by leveraging the tractability of tree-shaped models, we devise fast-converging conditional sampling algorithms for approximate inference, even though our theoretical analysis suggests that exact computation of marginals in the MoAT model is NP-hard. Empirically, MoAT achieves state-of-the-art performance on density estimation benchmarks when compared against powerful probabilistic models including hidden Chow-Liu Trees.

Certifying Fairness of Probabilistic Circuits

With the increased use of machine learning systems for decision making, questions about the fairness properties of such systems start to take center stage. Most existing work on algorithmic fairness assume complete observation of features at prediction time, as is the case for popular notions like statistical parity and equal opportunity. However, this is not sufficient for models that can make predictions with partial observation as we could miss patterns of bias and incorrectly certify a model to be fair. To address this, a recently introduced notion of fairness asks whether the model exhibits any discrimination pattern, in which an individual characterized by (partial) feature observations, receives vastly different decisions merely by disclosing one or more sensitive attributes such as gender and race. By explicitly accounting for partial observations, this provides a much more fine-grained notion of fairness. In this paper, we propose an algorithm to search for discrimination patterns in a general class of probabilistic models, namely probabilistic circuits. Previously, such algorithms were limited to naive Bayes classifiers which make strong independence assumptions; by contrast, probabilistic circuits provide a unifying framework for a wide range of tractable probabilistic models and can even be compiled from certain classes of Bayesian networks and probabilistic programs, making our method much more broadly applicable. Furthermore, for an unfair model, it may be useful to quickly find discrimination patterns and distill them for better interpretability. As such, we also propose a sampling-based approach to more efficiently mine discrimination patterns, and introduce new classes of patterns such as minimal, maximal, and Pareto optimal patterns that can effectively summarize exponentially many discrimination patterns

The Tail Wagging the Dog: Dataset Construction Biases of Social Bias Benchmarks

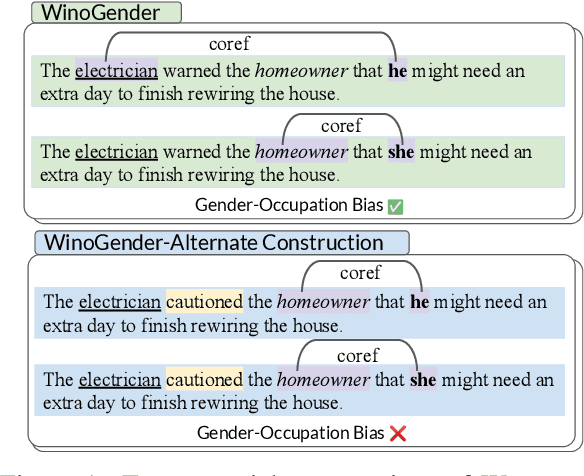
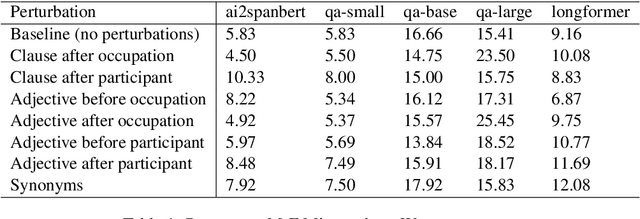
How reliably can we trust the scores obtained from social bias benchmarks as faithful indicators of problematic social biases in a given language model? In this work, we study this question by contrasting social biases with non-social biases stemming from choices made during dataset construction that might not even be discernible to the human eye. To do so, we empirically simulate various alternative constructions for a given benchmark based on innocuous modifications (such as paraphrasing or random-sampling) that maintain the essence of their social bias. On two well-known social bias benchmarks (Winogender and BiasNLI) we observe that these shallow modifications have a surprising effect on the resulting degree of bias across various models. We hope these troubling observations motivate more robust measures of social biases.