Scaling Probabilistic Circuits via Monarch Matrices

Probabilistic Circuits (PCs) are tractable representations of probability distributions allowing for exact and efficient computation of likelihoods and marginals. Recent advancements have improved the scalability of PCs either by leveraging their sparse properties or through the use of tensorized operations for better hardware utilization. However, no existing method fully exploits both aspects simultaneously. In this paper, we propose a novel sparse and structured parameterization for the sum blocks in PCs. By replacing dense matrices with sparse Monarch matrices, we significantly reduce the memory and computation costs, enabling unprecedented scaling of PCs. From a theory perspective, our construction arises naturally from circuit multiplication; from a practical perspective, compared to previous efforts on scaling up tractable probabilistic models, our approach not only achieves state-of-the-art generative modeling performance on challenging benchmarks like Text8, LM1B and ImageNet, but also demonstrates superior scaling behavior, achieving the same performance with substantially less compute as measured by the number of floating-point operations (FLOPs) during training.

Rethinking Probabilistic Circuit Parameter Learning

Probabilistic Circuits (PCs) offer a computationally scalable framework for generative modeling, supporting exact and efficient inference of a wide range of probabilistic queries. While recent advances have significantly improved the expressiveness and scalability of PCs, effectively training their parameters remains a challenge. In particular, a widely used optimization method, full-batch Expectation-Maximization (EM), requires processing the entire dataset before performing a single update, making it ineffective for large datasets. While empirical extensions to the mini-batch setting have been proposed, it remains unclear what objective these algorithms are optimizing, making it difficult to assess their theoretical soundness. This paper bridges the gap by establishing a novel connection between the general EM objective and the standard full-batch EM algorithm. Building on this, we derive a theoretically grounded generalization to the mini-batch setting and demonstrate its effectiveness through preliminary empirical results.

Plug-and-Play Context Feature Reuse for Efficient Masked Generation

Masked generative models (MGMs) have emerged as a powerful framework for image synthesis, combining parallel decoding with strong bidirectional context modeling. However, generating high-quality samples typically requires many iterative decoding steps, resulting in high inference costs. A straightforward way to speed up generation is by decoding more tokens in each step, thereby reducing the total number of steps. However, when many tokens are decoded simultaneously, the model can only estimate the univariate marginal distributions independently, failing to capture the dependency among them. As a result, reducing the number of steps significantly compromises generation fidelity. In this work, we introduce ReCAP (Reused Context-Aware Prediction), a plug-and-play module that accelerates inference in MGMs by constructing low-cost steps via reusing feature embeddings from previously decoded context tokens. ReCAP interleaves standard full evaluations with lightweight steps that cache and reuse context features, substantially reducing computation while preserving the benefits of fine-grained, iterative generation. We demonstrate its effectiveness on top of three representative MGMs (MaskGIT, MAGE, and MAR), including both discrete and continuous token spaces and covering diverse architectural designs. In particular, on ImageNet256 class-conditional generation, ReCAP achieves up to 2.4x faster inference than the base model with minimal performance drop, and consistently delivers better efficiency-fidelity trade-offs under various generation settings.

TRACE Back from the Future: A Probabilistic Reasoning Approach to Controllable Language Generation

As large language models (LMs) advance, there is an increasing need to control their outputs to align with human values (e.g., detoxification) or desired attributes (e.g., personalization, topic). However, autoregressive models focus on next-token predictions and struggle with global properties that require looking ahead. Existing solutions either tune or post-train LMs for each new attribute - expensive and inflexible - or approximate the Expected Attribute Probability (EAP) of future sequences by sampling or training, which is slow and unreliable for rare attributes. We introduce TRACE (Tractable Probabilistic Reasoning for Adaptable Controllable gEneration), a novel framework that efficiently computes EAP and adapts to new attributes through tractable probabilistic reasoning and lightweight control. TRACE distills a Hidden Markov Model (HMM) from an LM and pairs it with a small classifier to estimate attribute probabilities, enabling exact EAP computation over the HMM's predicted futures. This EAP is then used to reweigh the LM's next-token probabilities for globally compliant continuations. Empirically, TRACE achieves state-of-the-art results in detoxification with only 10% decoding overhead, adapts to 76 low-resource personalized LLMs within seconds, and seamlessly extends to composite attributes.

Adversarial Tokenization

Current LLM pipelines account for only one possible tokenization for a given string, ignoring exponentially many alternative tokenizations during training and inference. For example, the standard Llama3 tokenization of penguin is [p,enguin], yet [peng,uin] is another perfectly valid alternative. In this paper, we show that despite LLMs being trained solely on one tokenization, they still retain semantic understanding of other tokenizations, raising questions about their implications in LLM safety. Put succinctly, we answer the following question: can we adversarially tokenize an obviously malicious string to evade safety and alignment restrictions? We show that not only is adversarial tokenization an effective yet previously neglected axis of attack, but it is also competitive against existing state-of-the-art adversarial approaches without changing the text of the harmful request. We empirically validate this exploit across three state-of-the-art LLMs and adversarial datasets, revealing a previously unknown vulnerability in subword models.

Tractable Transformers for Flexible Conditional Generation

Non-autoregressive (NAR) generative models are valuable because they can handle diverse conditional generation tasks in a more principled way than their autoregressive (AR) counterparts, which are constrained by sequential dependency requirements. Recent advancements in NAR models, such as diffusion language models, have demonstrated superior performance in unconditional generation compared to AR models (e.g., GPTs) of similar sizes. However, such improvements do not always lead to improved conditional generation performance. We show that a key reason for this gap is the difficulty in generalizing to conditional probability queries unseen during training. As a result, strong unconditional generation performance does not guarantee high-quality conditional generation. This paper proposes Tractable Transformers (Tracformer), a Transformer-based generative model that is more robust to different conditional generation tasks. Unlike existing models that rely solely on global contextual features derived from full inputs, Tracformers incorporate a sparse Transformer encoder to capture both local and global contextual information. This information is routed through a decoder for conditional generation. Empirical results demonstrate that Tracformers achieve state-of-the-art conditional generation performance on text modeling compared to recent diffusion and AR model baselines.

Enabling Autoregressive Models to Fill In Masked Tokens

Historically, LLMs have been trained using either autoregressive (AR) or masked language modeling (MLM) objectives, with AR models gaining dominance in recent years. However, AR models are inherently incapable of masked infilling, which is the ability to predict masked tokens between past and future context. In contrast, MLM models suffer from intrinsic computational inefficiencies during both training and inference that hinder their scalability. This work introduces MARIA (Masked and Autoregressive Infilling Architecture), a novel approach that leverages the strengths of both paradigms to achieve state-of-the-art masked infilling performance. MARIA combines a pre-trained MLM and AR model by training a linear decoder that takes their concatenated hidden states as input. This minimal modification enables the AR model to perform infilling while retaining its inherent advantages in terms of faster inference with KV caching. Our results demonstrate that MARIA significantly outperforms existing methods, namely discrete diffusion models, on masked infilling tasks.

Deep Generative Models with Hard Linear Equality Constraints

While deep generative models~(DGMs) have demonstrated remarkable success in capturing complex data distributions, they consistently fail to learn constraints that encode domain knowledge and thus require constraint integration. Existing solutions to this challenge have primarily relied on heuristic methods and often ignore the underlying data distribution, harming the generative performance. In this work, we propose a probabilistically sound approach for enforcing the hard constraints into DGMs to generate constraint-compliant and realistic data. This is achieved by our proposed gradient estimators that allow the constrained distribution, the data distribution conditioned on constraints, to be differentiably learned. We carry out extensive experiments with various DGM model architectures over five image datasets and three scientific applications in which domain knowledge is governed by linear equality constraints. We validate that the standard DGMs almost surely generate data violating the constraints. Among all the constraint integration strategies, ours not only guarantees the satisfaction of constraints in generation but also archives superior generative performance than the other methods across every benchmark.

A Compositional Atlas for Algebraic Circuits

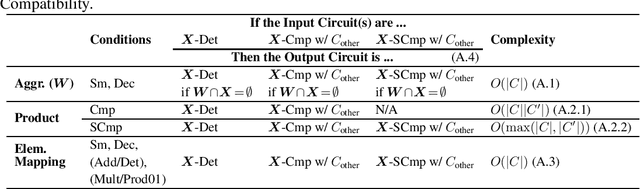
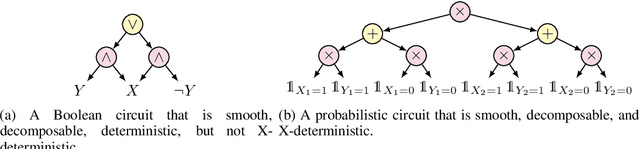
Circuits based on sum-product structure have become a ubiquitous representation to compactly encode knowledge, from Boolean functions to probability distributions. By imposing constraints on the structure of such circuits, certain inference queries become tractable, such as model counting and most probable configuration. Recent works have explored analyzing probabilistic and causal inference queries as compositions of basic operators to derive tractability conditions. In this paper, we take an algebraic perspective for compositional inference, and show that a large class of queries - including marginal MAP, probabilistic answer set programming inference, and causal backdoor adjustment - correspond to a combination of basic operators over semirings: aggregation, product, and elementwise mapping. Using this framework, we uncover simple and general sufficient conditions for tractable composition of these operators, in terms of circuit properties (e.g., marginal determinism, compatibility) and conditions on the elementwise mappings. Applying our analysis, we derive novel tractability conditions for many such compositional queries. Our results unify tractability conditions for existing problems on circuits, while providing a blueprint for analysing novel compositional inference queries.

Restructuring Tractable Probabilistic Circuits

Probabilistic circuits (PCs) is a unifying representation for probabilistic models that support tractable inference. Numerous applications of PCs like controllable text generation depend on the ability to efficiently multiply two circuits. Existing multiplication algorithms require that the circuits respect the same structure, i.e. variable scopes decomposes according to the same vtree. In this work, we propose and study the task of restructuring structured(-decomposable) PCs, that is, transforming a structured PC such that it conforms to a target vtree. We propose a generic approach for this problem and show that it leads to novel polynomial-time algorithms for multiplying circuits respecting different vtrees, as well as a practical depth-reduction algorithm that preserves structured decomposibility. Our work opens up new avenues for tractable PC inference, suggesting the possibility of training with less restrictive PC structures while enabling efficient inference by changing their structures at inference time.