A Compositional Atlas for Algebraic Circuits

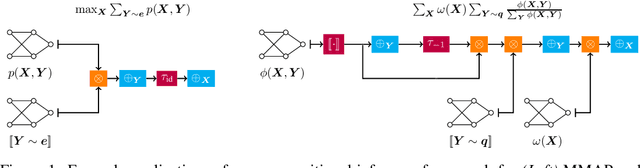
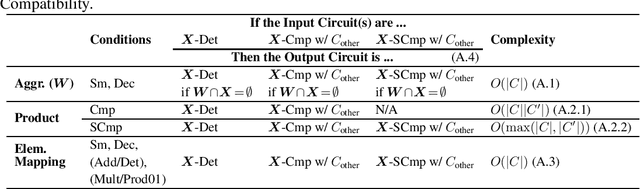
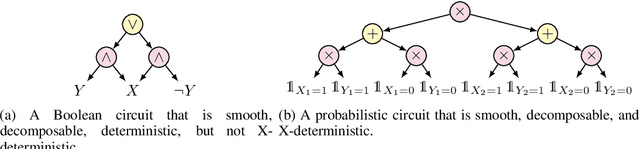
Circuits based on sum-product structure have become a ubiquitous representation to compactly encode knowledge, from Boolean functions to probability distributions. By imposing constraints on the structure of such circuits, certain inference queries become tractable, such as model counting and most probable configuration. Recent works have explored analyzing probabilistic and causal inference queries as compositions of basic operators to derive tractability conditions. In this paper, we take an algebraic perspective for compositional inference, and show that a large class of queries - including marginal MAP, probabilistic answer set programming inference, and causal backdoor adjustment - correspond to a combination of basic operators over semirings: aggregation, product, and elementwise mapping. Using this framework, we uncover simple and general sufficient conditions for tractable composition of these operators, in terms of circuit properties (e.g., marginal determinism, compatibility) and conditions on the elementwise mappings. Applying our analysis, we derive novel tractability conditions for many such compositional queries. Our results unify tractability conditions for existing problems on circuits, while providing a blueprint for analysing novel compositional inference queries.

Assessing Good, Bad and Ugly Arguments Generated by ChatGPT: a New Dataset, its Methodology and Associated Tasks

The recent success of Large Language Models (LLMs) has sparked concerns about their potential to spread misinformation. As a result, there is a pressing need for tools to identify ``fake arguments'' generated by such models. To create these tools, examples of texts generated by LLMs are needed. This paper introduces a methodology to obtain good, bad and ugly arguments from argumentative essays produced by ChatGPT, OpenAI's LLM. We then describe a novel dataset containing a set of diverse arguments, ArGPT. We assess the effectiveness of our dataset and establish baselines for several argumentation-related tasks. Finally, we show that the artificially generated data relates well to human argumentation and thus is useful as a tool to train and test systems for the defined tasks.

dPASP: A Comprehensive Differentiable Probabilistic Answer Set Programming Environment For Neurosymbolic Learning and Reasoning

We present dPASP, a novel declarative probabilistic logic programming framework for differentiable neuro-symbolic reasoning. The framework allows for the specification of discrete probabilistic models with neural predicates, logic constraints and interval-valued probabilistic choices, thus supporting models that combine low-level perception (images, texts, etc), common-sense reasoning, and (vague) statistical knowledge. To support all such features, we discuss the several semantics for probabilistic logic programs that can express nondeterministic, contradictory, incomplete and/or statistical knowledge. We also discuss how gradient-based learning can be performed with neural predicates and probabilistic choices under selected semantics. We then describe an implemented package that supports inference and learning in the language, along with several example programs. The package requires minimal user knowledge of deep learning system's inner workings, while allowing end-to-end training of rather sophisticated models and loss functions.

Integrating question answering and text-to-SQL in Portuguese

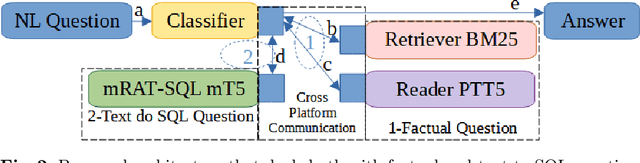
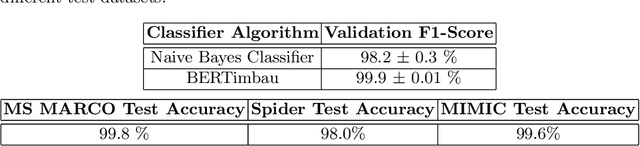
Deep learning transformers have drastically improved systems that automatically answer questions in natural language. However, different questions demand different answering techniques; here we propose, build and validate an architecture that integrates different modules to answer two distinct kinds of queries. Our architecture takes a free-form natural language text and classifies it to send it either to a Neural Question Answering Reasoner or a Natural Language parser to SQL. We implemented a complete system for the Portuguese language, using some of the main tools available for the language and translating training and testing datasets. Experiments show that our system selects the appropriate answering method with high accuracy (over 99\%), thus validating a modular question answering strategy.

Tractable Inference in Credal Sentential Decision Diagrams

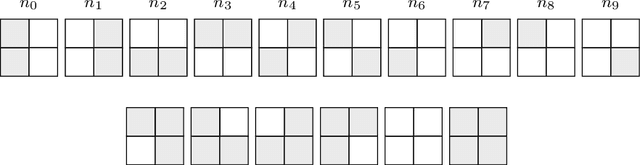
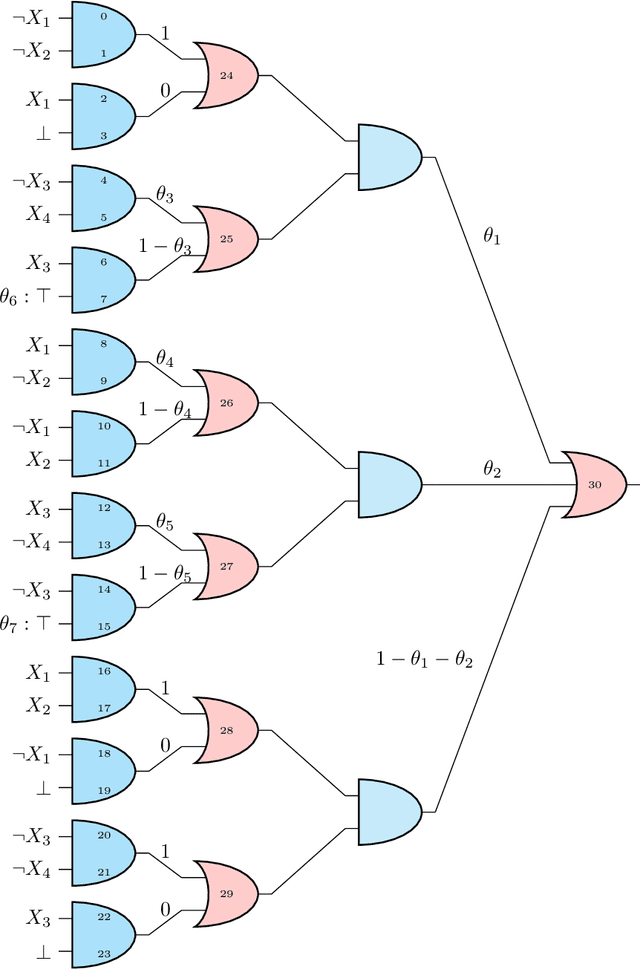
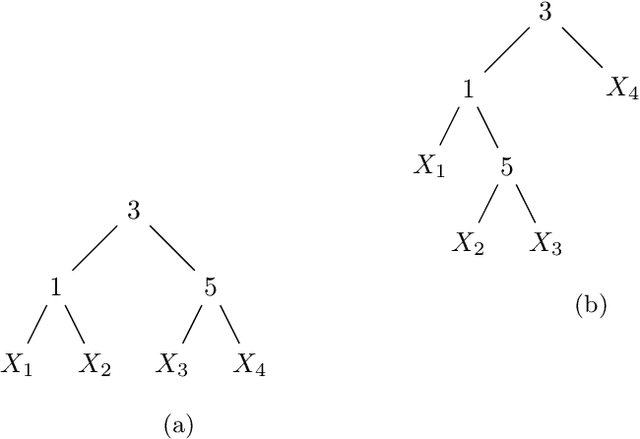
Probabilistic sentential decision diagrams are logic circuits where the inputs of disjunctive gates are annotated by probability values. They allow for a compact representation of joint probability mass functions defined over sets of Boolean variables, that are also consistent with the logical constraints defined by the circuit. The probabilities in such a model are usually learned from a set of observations. This leads to overconfident and prior-dependent inferences when data are scarce, unreliable or conflicting. In this work, we develop the credal sentential decision diagrams, a generalisation of their probabilistic counterpart that allows for replacing the local probabilities with (so-called credal) sets of mass functions. These models induce a joint credal set over the set of Boolean variables, that sharply assigns probability zero to states inconsistent with the logical constraints. Three inference algorithms are derived for these models, these allow to compute: (i) the lower and upper probabilities of an observation for an arbitrary number of variables; (ii) the lower and upper conditional probabilities for the state of a single variable given an observation; (iii) whether or not all the probabilistic sentential decision diagrams compatible with the credal specification have the same most probable explanation of a given set of variables given an observation of the other variables. These inferences are tractable, as all the three algorithms, based on bottom-up traversal with local linear programming tasks on the disjunctive gates, can be solved in polynomial time with respect to the circuit size. For a first empirical validation, we consider a simple application based on noisy seven-segment display images. The credal models are observed to properly distinguish between easy and hard-to-detect instances and outperform other generative models not able to cope with logical constraints.

On the Semantics and Complexity of Probabilistic Logic Programs

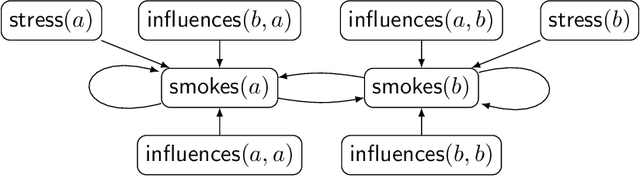
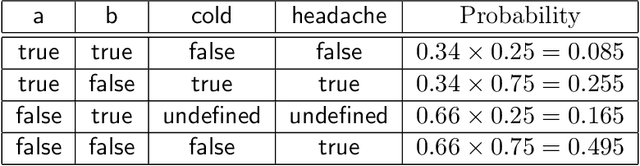
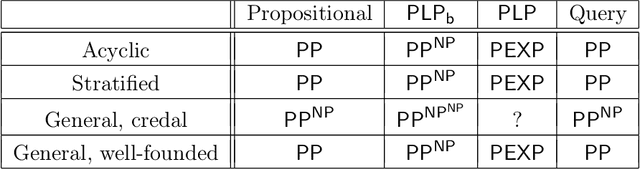
We examine the meaning and the complexity of probabilistic logic programs that consist of a set of rules and a set of independent probabilistic facts (that is, programs based on Sato's distribution semantics). We focus on two semantics, respectively based on stable and on well-founded models. We show that the semantics based on stable models (referred to as the "credal semantics") produces sets of probability models that dominate infinitely monotone Choquet capacities, we describe several useful consequences of this result. We then examine the complexity of inference with probabilistic logic programs. We distinguish between the complexity of inference when a probabilistic program and a query are given (the inferential complexity), and the complexity of inference when the probabilistic program is fixed and the query is given (the query complexity, akin to data complexity as used in database theory). We obtain results on the inferential and query complexity for acyclic, stratified, and cyclic propositional and relational programs, complexity reaches various levels of the counting hierarchy and even exponential levels.

The Complexity of Bayesian Networks Specified by Propositional and Relational Languages

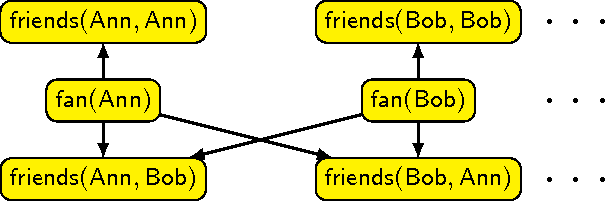
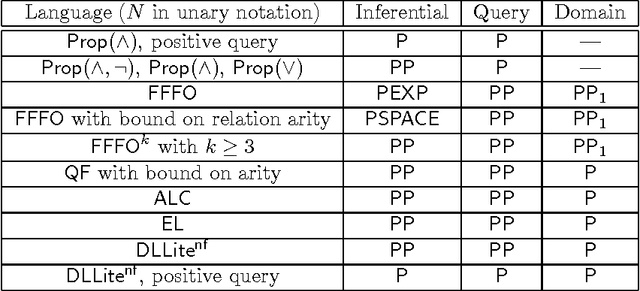
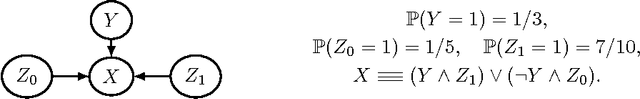
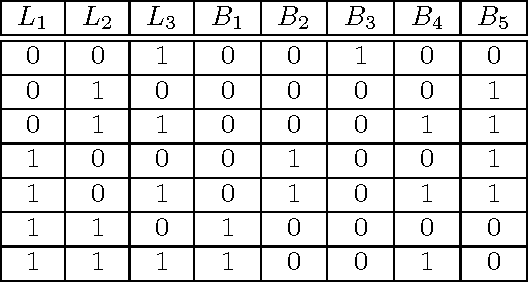
We examine the complexity of inference in Bayesian networks specified by logical languages. We consider representations that range from fragments of propositional logic to function-free first-order logic with equality; in doing so we cover a variety of plate models and of probabilistic relational models. We study the complexity of inferences when network, query and domain are the input (the inferential and the combined complexity), when the network is fixed and query and domain are the input (the query/data complexity), and when the network and query are fixed and the domain is the input (the domain complexity). We draw connections with probabilistic databases and liftability results, and obtain complexity classes that range from polynomial to exponential levels.

Solving Limited Memory Influence Diagrams

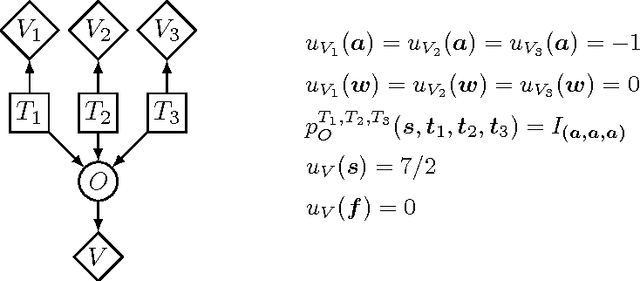
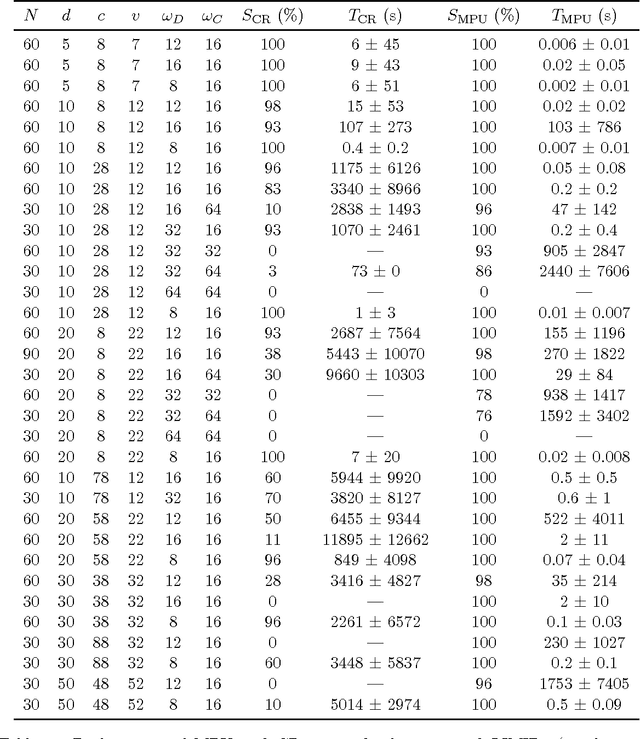
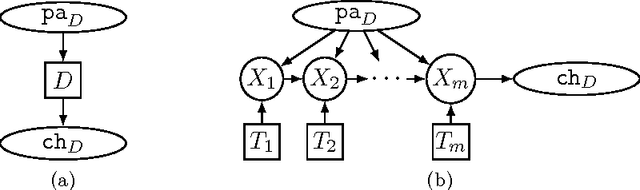
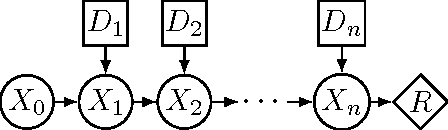
We present a new algorithm for exactly solving decision making problems represented as influence diagrams. We do not require the usual assumptions of no forgetting and regularity; this allows us to solve problems with simultaneous decisions and limited information. The algorithm is empirically shown to outperform a state-of-the-art algorithm on randomly generated problems of up to 150 variables and $10^{64}$ solutions. We show that the problem is NP-hard even if the underlying graph structure of the problem has small treewidth and the variables take on a bounded number of states, but that a fully polynomial time approximation scheme exists for these cases. Moreover, we show that the bound on the number of states is a necessary condition for any efficient approximation scheme.