Advances in Learning Bayesian Networks of Bounded Treewidth

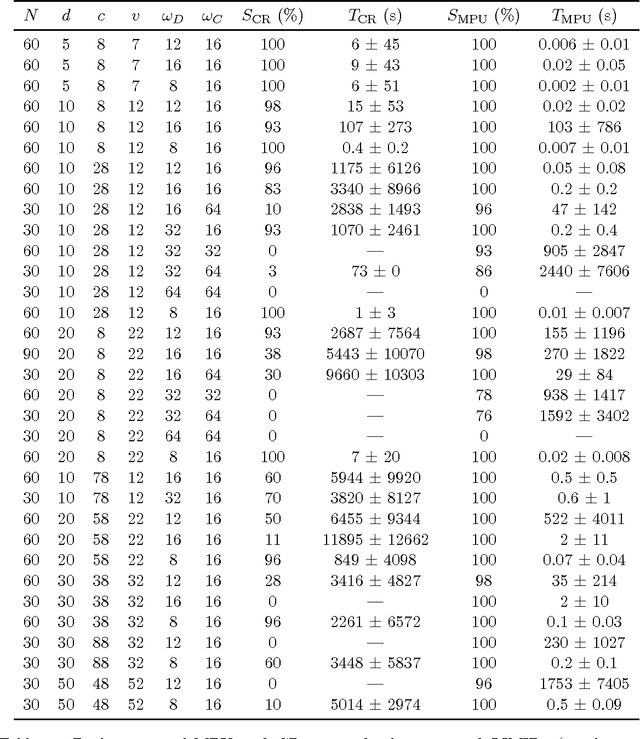
This work presents novel algorithms for learning Bayesian network structures with bounded treewidth. Both exact and approximate methods are developed. The exact method combines mixed-integer linear programming formulations for structure learning and treewidth computation. The approximate method consists in uniformly sampling $k$-trees (maximal graphs of treewidth $k$), and subsequently selecting, exactly or approximately, the best structure whose moral graph is a subgraph of that $k$-tree. Some properties of these methods are discussed and proven. The approaches are empirically compared to each other and to a state-of-the-art method for learning bounded treewidth structures on a collection of public data sets with up to 100 variables. The experiments show that our exact algorithm outperforms the state of the art, and that the approximate approach is fairly accurate.

On the Complexity of Strong and Epistemic Credal Networks

Credal networks are graph-based statistical models whose parameters take values in a set, instead of being sharply specified as in traditional statistical models (e.g., Bayesian networks). The computational complexity of inferences on such models depends on the irrelevance/independence concept adopted. In this paper, we study inferential complexity under the concepts of epistemic irrelevance and strong independence. We show that inferences under strong independence are NP-hard even in trees with ternary variables. We prove that under epistemic irrelevance the polynomial time complexity of inferences in credal trees is not likely to extend to more general models (e.g. singly connected networks). These results clearly distinguish networks that admit efficient inferences and those where inferences are most likely hard, and settle several open questions regarding computational complexity.

Inference in Polytrees with Sets of Probabilities

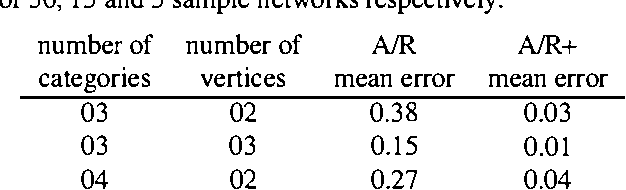
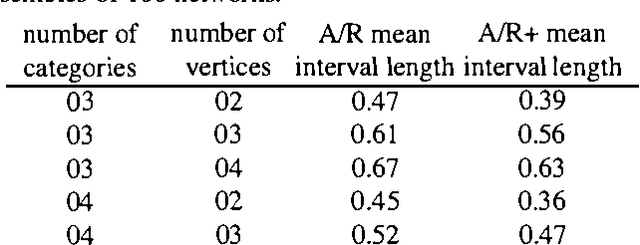
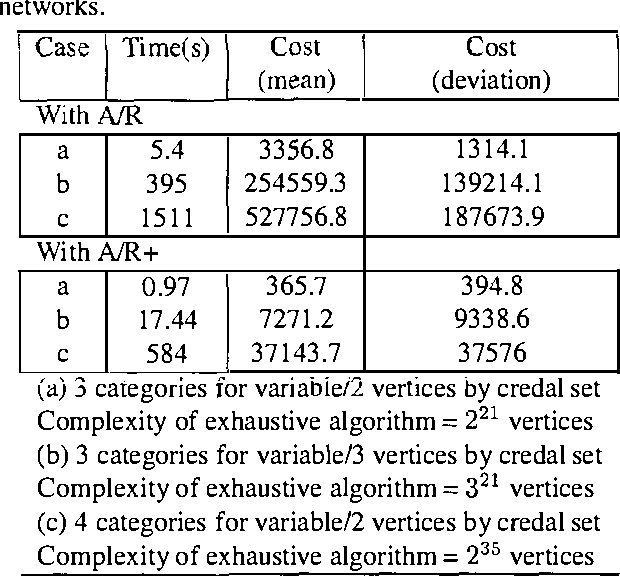
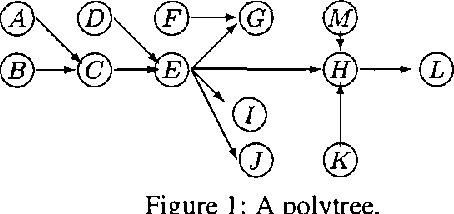
Inferences in directed acyclic graphs associated with probability sets and probability intervals are NP-hard, even for polytrees. In this paper we focus on such inferences, and propose: 1) a substantial improvement on Tessems A / R algorithm FOR polytrees WITH probability intervals; 2) a new algorithm FOR direction - based local search(IN sets OF probability) that improves ON existing methods; 3) a collection OF branch - AND - bound algorithms that combine the previous techniques.The first two techniques lead TO approximate solutions, WHILE branch - AND - bound procedures can produce either exact OR approximate solutions.We report ON dramatic improvements ON existing techniques FOR inference WITH probability sets AND intervals, IN SOME cases reducing the computational effort BY many orders OF magnitude.

The Complexity of Approximately Solving Influence Diagrams

Influence diagrams allow for intuitive and yet precise description of complex situations involving decision making under uncertainty. Unfortunately, most of the problems described by influence diagrams are hard to solve. In this paper we discuss the complexity of approximately solving influence diagrams. We do not assume no-forgetting or regularity, which makes the class of problems we address very broad. Remarkably, we show that when both the tree-width and the cardinality of the variables are bounded the problem admits a fully polynomial-time approximation scheme.

Propositional and Relational Bayesian Networks Associated with Imprecise and Qualitative Probabilistic Assesments

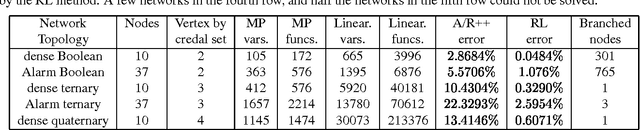
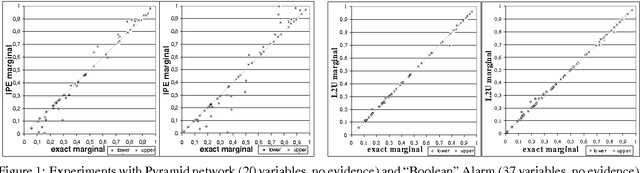
This paper investigates a representation language with flexibility inspired by probabilistic logic and compactness inspired by relational Bayesian networks. The goal is to handle propositional and first-order constructs together with precise, imprecise, indeterminate and qualitative probabilistic assessments. The paper shows how this can be achieved through the theory of credal networks. New exact and approximate inference algorithms based on multilinear programming and iterated/loopy propagation of interval probabilities are presented; their superior performance, compared to existing ones, is shown empirically.

Belief Updating and Learning in Semi-Qualitative Probabilistic Networks

This paper explores semi-qualitative probabilistic networks (SQPNs) that combine numeric and qualitative information. We first show that exact inferences with SQPNs are NPPP-Complete. We then show that existing qualitative relations in SQPNs (plus probabilistic logic and imprecise assessments) can be dealt effectively through multilinear programming. We then discuss learning: we consider a maximum likelihood method that generates point estimates given a SQPN and empirical data, and we describe a Bayesian-minded method that employs the Imprecise Dirichlet Model to generate set-valued estimates.

Strategy Selection in Influence Diagrams using Imprecise Probabilities

This paper describes a new algorithm to solve the decision making problem in Influence Diagrams based on algorithms for credal networks. Decision nodes are associated to imprecise probability distributions and a reformulation is introduced that finds the global maximum strategy with respect to the expected utility. We work with Limited Memory Influence Diagrams, which generalize most Influence Diagram proposals and handle simultaneous decisions. Besides the global optimum method, we explore an anytime approximate solution with a guaranteed maximum error and show that imprecise probabilities are handled in a straightforward way. Complexity issues and experiments with random diagrams and an effects-based military planning problem are discussed.

Solving Limited Memory Influence Diagrams

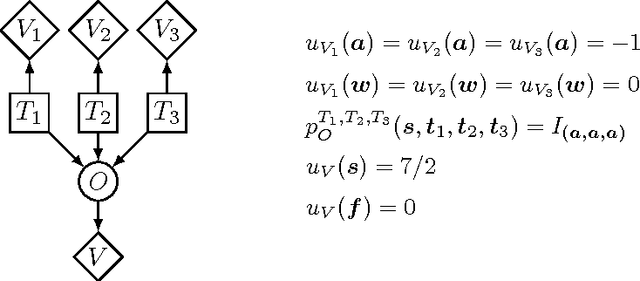
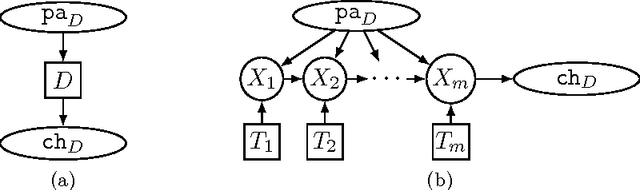
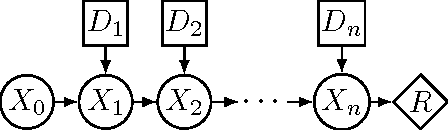
We present a new algorithm for exactly solving decision making problems represented as influence diagrams. We do not require the usual assumptions of no forgetting and regularity; this allows us to solve problems with simultaneous decisions and limited information. The algorithm is empirically shown to outperform a state-of-the-art algorithm on randomly generated problems of up to 150 variables and $10^{64}$ solutions. We show that the problem is NP-hard even if the underlying graph structure of the problem has small treewidth and the variables take on a bounded number of states, but that a fully polynomial time approximation scheme exists for these cases. Moreover, we show that the bound on the number of states is a necessary condition for any efficient approximation scheme.