Constraint- and Score-Based Nonlinear Granger Causality Discovery with Kernels

Kernel-based methods are used in the context of Granger Causality to enable the identification of nonlinear causal relationships between time series variables. In this paper, we show that two state of the art kernel-based Granger Causality (GC) approaches can be theoretically unified under the framework of Kernel Principal Component Regression (KPCR), and introduce a method based on this unification, demonstrating that this approach can improve causal identification. Additionally, we introduce a Gaussian Process score-based model with Smooth Information Criterion penalisation on the marginal likelihood, and demonstrate improved performance over existing state of the art time-series nonlinear causal discovery methods. Furthermore, we propose a contemporaneous causal identification algorithm, fully based on GC, using the proposed score-based $GP_{SIC}$ method, and compare its performance to a state of the art contemporaneous time series causal discovery algorithm.

Why AI Safety Requires Uncertainty, Incomplete Preferences, and Non-Archimedean Utilities

How can we ensure that AI systems are aligned with human values and remain safe? We can study this problem through the frameworks of the AI assistance and the AI shutdown games. The AI assistance problem concerns designing an AI agent that helps a human to maximise their utility function(s). However, only the human knows these function(s); the AI assistant must learn them. The shutdown problem instead concerns designing AI agents that: shut down when a shutdown button is pressed; neither try to prevent nor cause the pressing of the shutdown button; and otherwise accomplish their task competently. In this paper, we show that addressing these challenges requires AI agents that can reason under uncertainty and handle both incomplete and non-Archimedean preferences.

dynoGP: Deep Gaussian Processes for dynamic system identification

In this work, we present a novel approach to system identification for dynamical systems, based on a specific class of Deep Gaussian Processes (Deep GPs). These models are constructed by interconnecting linear dynamic GPs (equivalent to stochastic linear time-invariant dynamical systems) and static GPs (to model static nonlinearities). Our approach combines the strengths of data-driven methods, such as those based on neural network architectures, with the ability to output a probability distribution. This offers a more comprehensive framework for system identification that includes uncertainty quantification. Using both simulated and real-world data, we demonstrate the effectiveness of the proposed approach.

A tutorial on learning from preferences and choices with Gaussian Processes

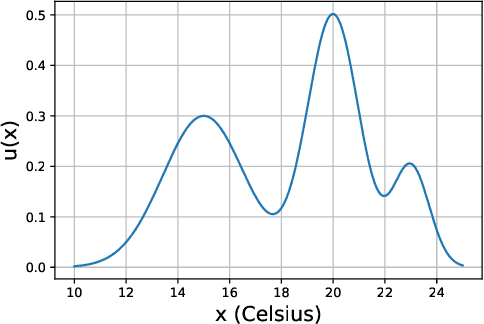
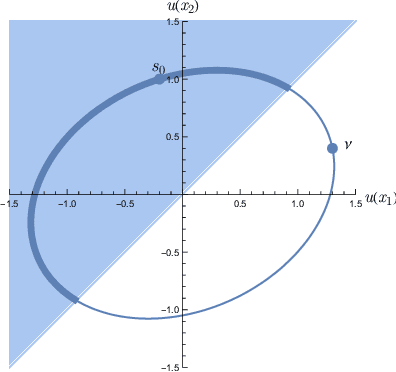
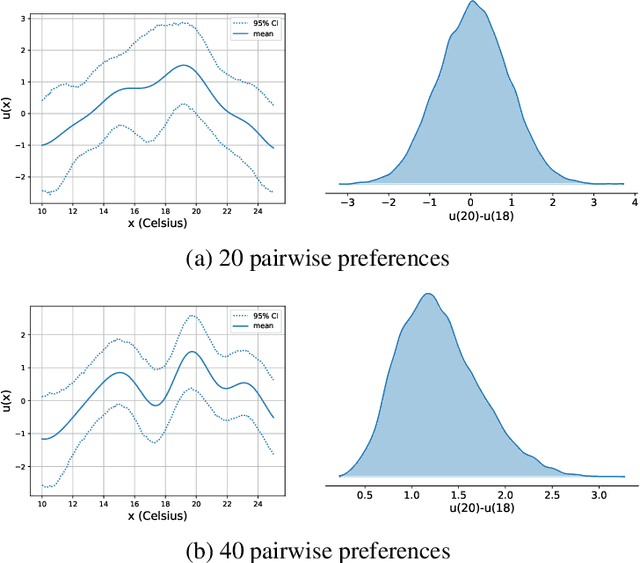
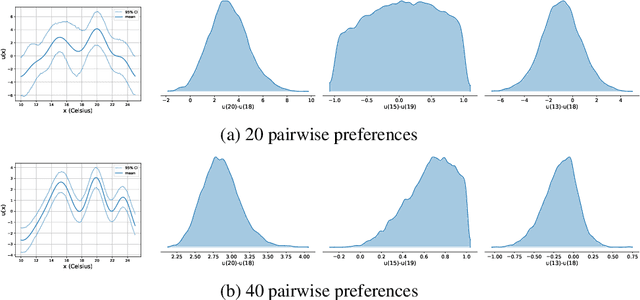
Preference modelling lies at the intersection of economics, decision theory, machine learning and statistics. By understanding individuals' preferences and how they make choices, we can build products that closely match their expectations, paving the way for more efficient and personalised applications across a wide range of domains. The objective of this tutorial is to present a cohesive and comprehensive framework for preference learning with Gaussian Processes (GPs), demonstrating how to seamlessly incorporate rationality principles (from economics and decision theory) into the learning process. By suitably tailoring the likelihood function, this framework enables the construction of preference learning models that encompass random utility models, limits of discernment, and scenarios with multiple conflicting utilities for both object- and label-preference. This tutorial builds upon established research while simultaneously introducing some novel GP-based models to address specific gaps in the existing literature.

Learning Choice Functions with Gaussian Processes

In consumer theory, ranking available objects by means of preference relations yields the most common description of individual choices. However, preference-based models assume that individuals: (1) give their preferences only between pairs of objects; (2) are always able to pick the best preferred object. In many situations, they may be instead choosing out of a set with more than two elements and, because of lack of information and/or incomparability (objects with contradictory characteristics), they may not able to select a single most preferred object. To address these situations, we need a choice-model which allows an individual to express a set-valued choice. Choice functions provide such a mathematical framework. We propose a Gaussian Process model to learn choice functions from choice-data. The proposed model assumes a multiple utility representation of a choice function based on the concept of Pareto rationalization, and derives a strategy to learn both the number and the values of these latent multiple utilities. Simulation experiments demonstrate that the proposed model outperforms the state-of-the-art methods.

Credal Valuation Networks for Machine Reasoning Under Uncertainty

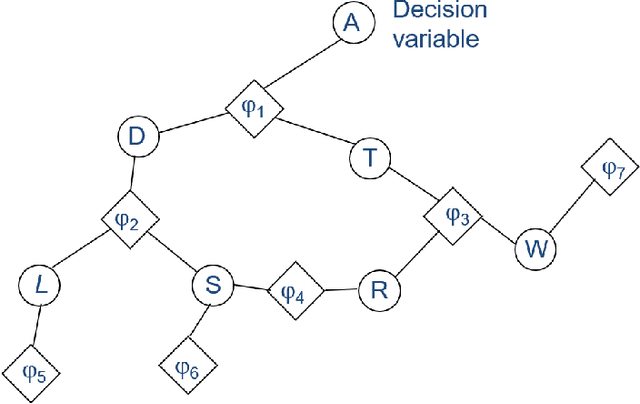
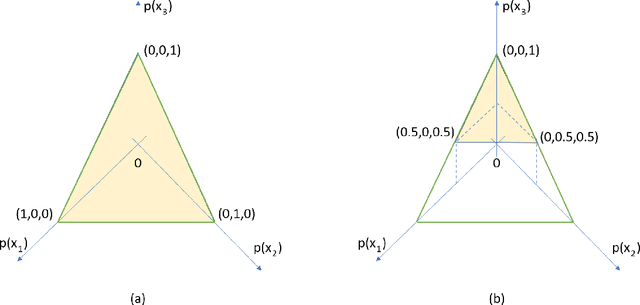
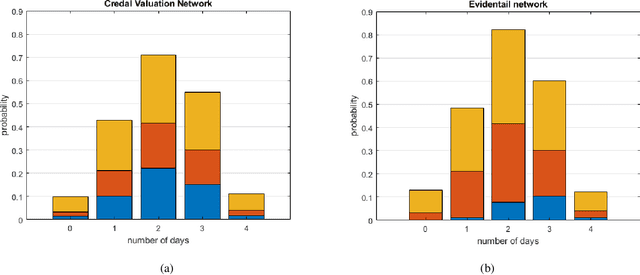
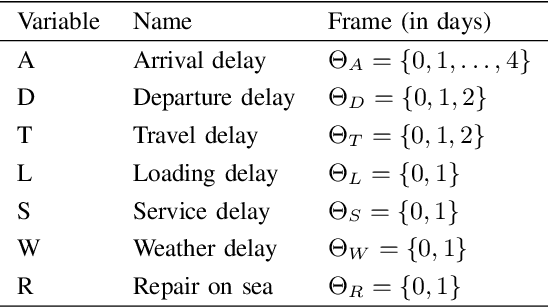
Contemporary undertakings provide limitless opportunities for widespread application of machine reasoning and artificial intelligence in situations characterised by uncertainty, hostility and sheer volume of data. The paper develops a valuation network as a graphical system for higher-level fusion and reasoning under uncertainty in support of the human operators. Valuations, which are mathematical representation of (uncertain) knowledge and collected data, are expressed as credal sets, defined as coherent interval probabilities in the framework of imprecise probability theory. The basic operations with such credal sets, combination and marginalisation, are defined to satisfy the axioms of a valuation algebra. A practical implementation of the credal valuation network is discussed and its utility demonstrated on a small scale example.

Correlated Product of Experts for Sparse Gaussian Process Regression

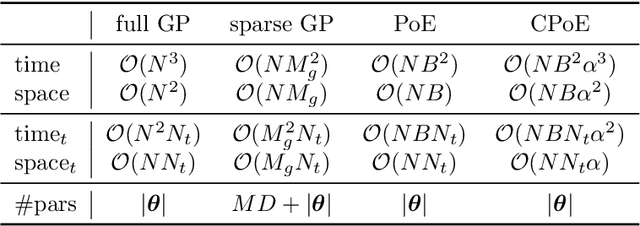
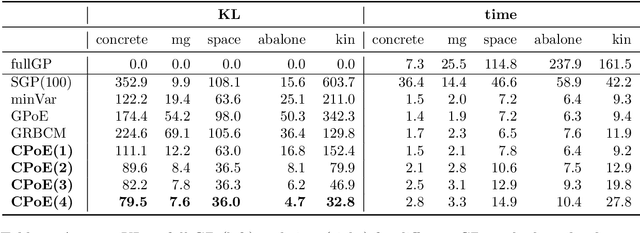
Gaussian processes (GPs) are an important tool in machine learning and statistics with applications ranging from social and natural science through engineering. They constitute a powerful kernelized non-parametric method with well-calibrated uncertainty estimates, however, off-the-shelf GP inference procedures are limited to datasets with several thousand data points because of their cubic computational complexity. For this reason, many sparse GPs techniques have been developed over the past years. In this paper, we focus on GP regression tasks and propose a new approach based on aggregating predictions from several local and correlated experts. Thereby, the degree of correlation between the experts can vary between independent up to fully correlated experts. The individual predictions of the experts are aggregated taking into account their correlation resulting in consistent uncertainty estimates. Our method recovers independent Product of Experts, sparse GP and full GP in the limiting cases. The presented framework can deal with a general kernel function and multiple variables, and has a time and space complexity which is linear in the number of experts and data samples, which makes our approach highly scalable. We demonstrate superior performance, in a time vs. accuracy sense, of our proposed method against state-of-the-art GP approximation methods for synthetic as well as several real-world datasets with deterministic and stochastic optimization.

Choice functions based multi-objective Bayesian optimisation

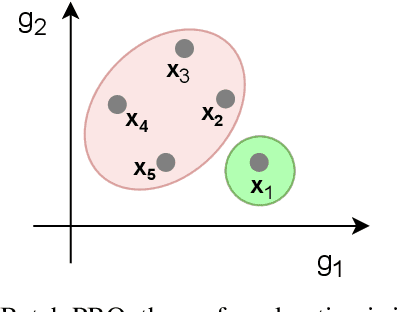
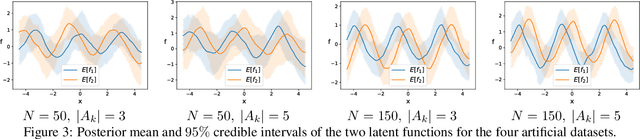
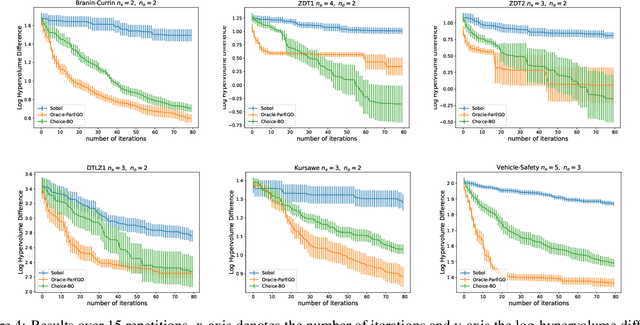
In this work we introduce a new framework for multi-objective Bayesian optimisation where the multi-objective functions can only be accessed via choice judgements, such as ``I pick options A,B,C among this set of five options A,B,C,D,E''. The fact that the option D is rejected means that there is at least one option among the selected ones A,B,C that I strictly prefer over D (but I do not have to specify which one). We assume that there is a latent vector function f for some dimension $n_e$ which embeds the options into the real vector space of dimension n, so that the choice set can be represented through a Pareto set of non-dominated options. By placing a Gaussian process prior on f and deriving a novel likelihood model for choice data, we propose a Bayesian framework for choice functions learning. We then apply this surrogate model to solve a novel multi-objective Bayesian optimisation from choice data problem.

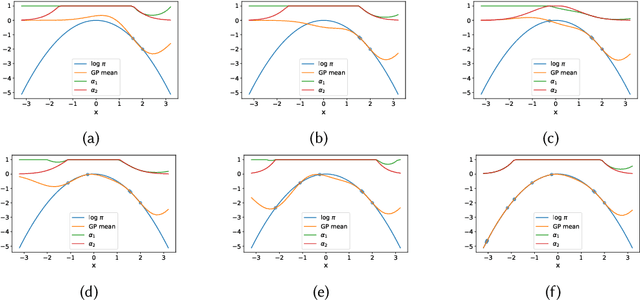
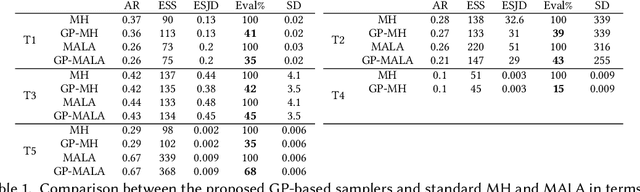
Gaussian Processes to speed up MCMC with automatic exploratory-exploitation effect

We present a two-stage Metropolis-Hastings algorithm for sampling probabilistic models, whose log-likelihood is computationally expensive to evaluate, by using a surrogate Gaussian Process (GP) model. The key feature of the approach, and the difference w.r.t. previous works, is the ability to learn the target distribution from scratch (while sampling), and so without the need of pre-training the GP. This is fundamental for automatic and inference in Probabilistic Programming Languages In particular, we present an alternative first stage acceptance scheme by marginalising out the GP distributed function, which makes the acceptance ratio explicitly dependent on the variance of the GP. This approach is extended to Metropolis-Adjusted Langevin algorithm (MALA).

Bayesian Optimisation for Sequential Experimental Design with Applications in Additive Manufacturing

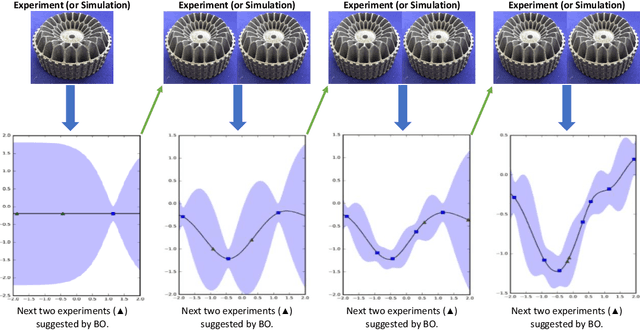
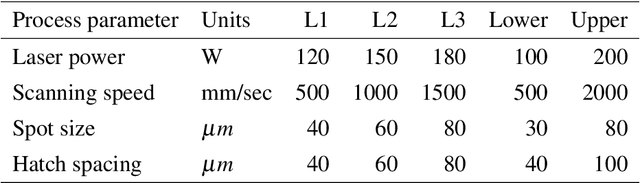
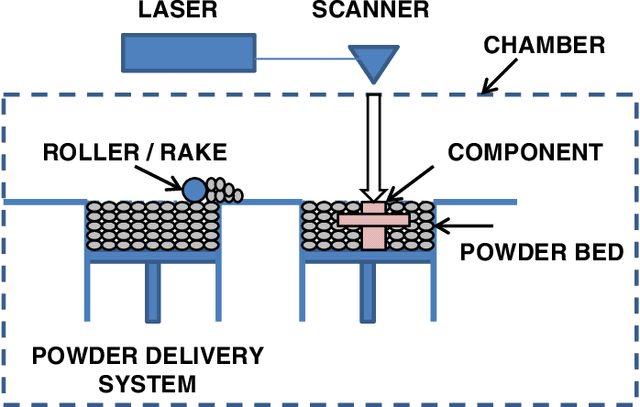
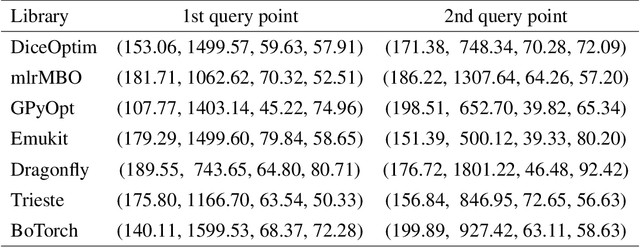
Bayesian optimization (BO) is an approach to globally optimizing black-box objective functions that are expensive to evaluate. BO-powered experimental design has found wide application in materials science, chemistry, experimental physics, drug development, etc. This work aims to bring attention to the benefits of applying BO in designing experiments and to provide a BO manual, covering both methodology and software, for the convenience of anyone who wants to apply or learn BO. In particular, we briefly explain the BO technique, review all the applications of BO in additive manufacturing, compare and exemplify the features of different open BO libraries, unlock new potential applications of BO to other types of data (e.g., preferential output). This article is aimed at readers with some understanding of Bayesian methods, but not necessarily with knowledge of additive manufacturing; the software performance overview and implementation instructions are instrumental for any experimental-design practitioner. Moreover, our review in the field of additive manufacturing highlights the current knowledge and technological trends of BO.