Forecasting intermittent time series with Gaussian Processes and Tweedie likelihood

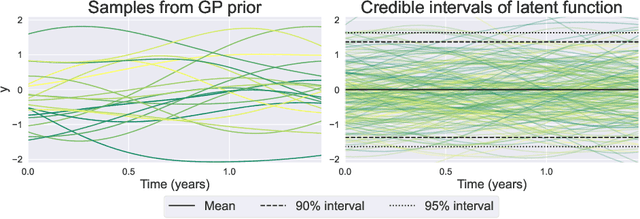
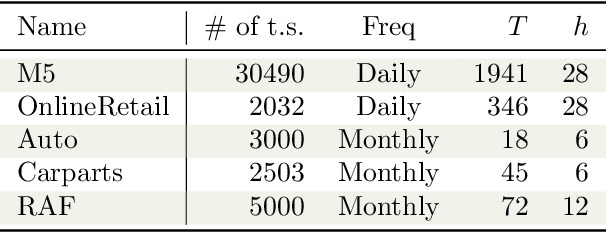
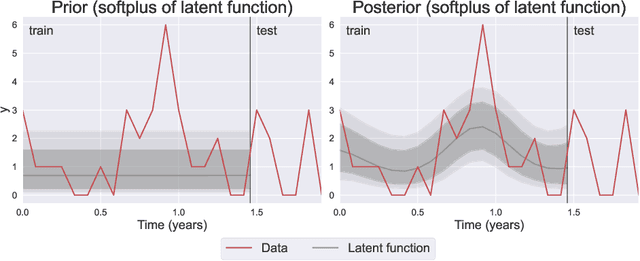
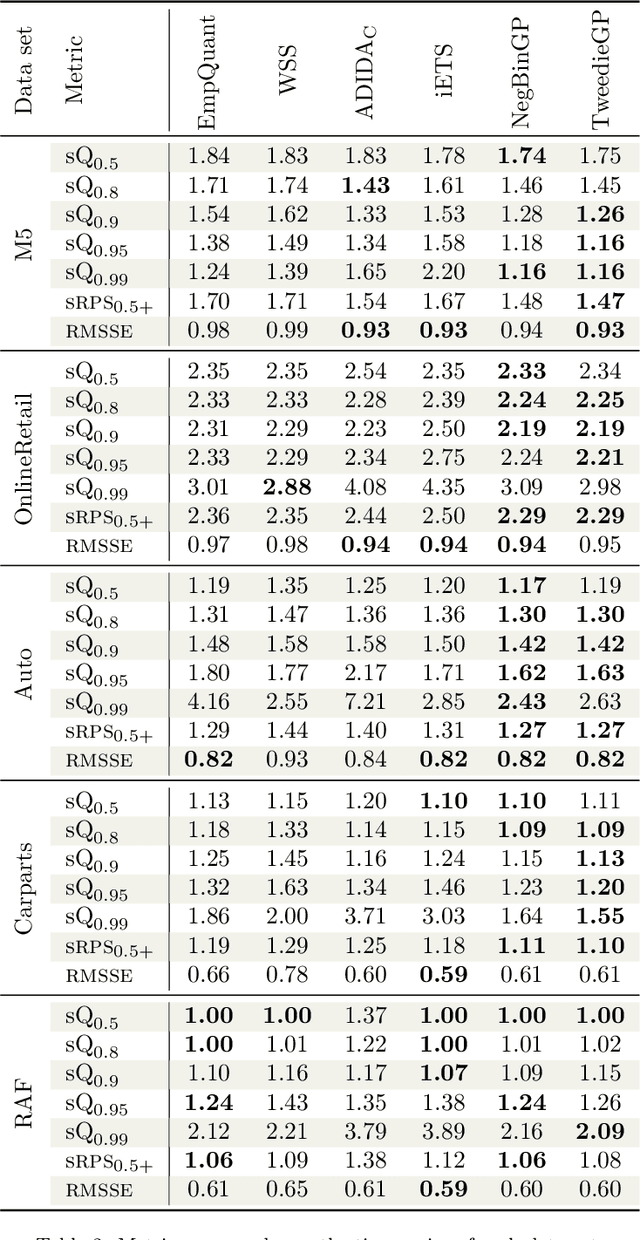
We introduce the use of Gaussian Processes (GPs) for the probabilistic forecasting of intermittent time series. The model is trained in a Bayesian framework that accounts for the uncertainty about the latent function and marginalizes it out when making predictions. We couple the latent GP variable with two types of forecast distributions: the negative binomial (NegBinGP) and the Tweedie distribution (TweedieGP). While the negative binomial has already been used in forecasting intermittent time series, this is the first time in which a fully parameterized Tweedie density is used for intermittent time series. We properly evaluate the Tweedie density, which is both zero-inflated and heavy tailed, avoiding simplifying assumptions made in existing models. We test our models on thousands of intermittent count time series. Results show that our models provide consistently better probabilistic forecasts than the competitors. In particular, TweedieGP obtains the best estimates of the highest quantiles, thus showing that it is more flexible than NegBinGP.

A tutorial on learning from preferences and choices with Gaussian Processes

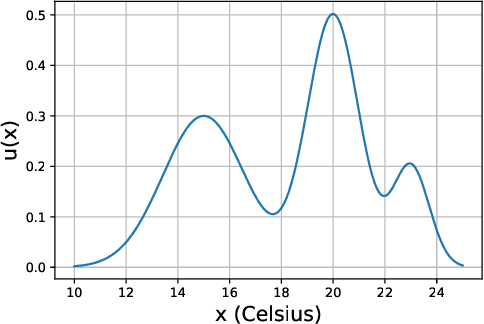
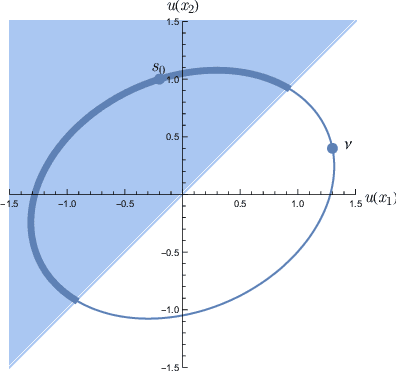
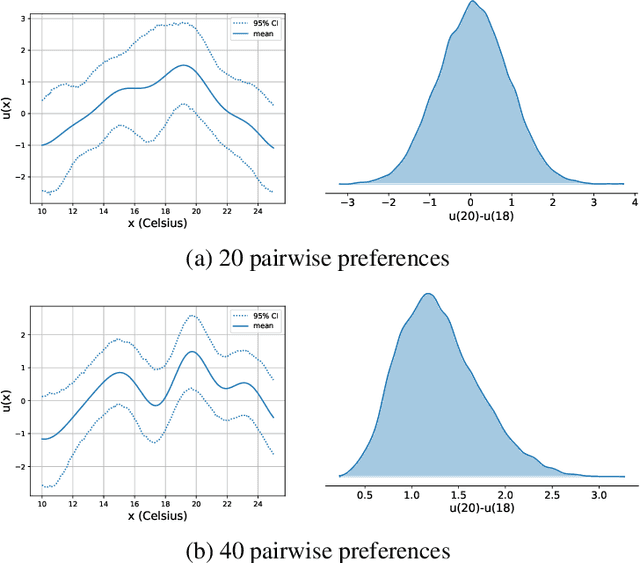
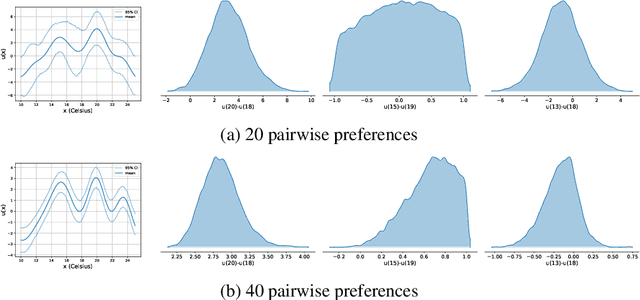
Preference modelling lies at the intersection of economics, decision theory, machine learning and statistics. By understanding individuals' preferences and how they make choices, we can build products that closely match their expectations, paving the way for more efficient and personalised applications across a wide range of domains. The objective of this tutorial is to present a cohesive and comprehensive framework for preference learning with Gaussian Processes (GPs), demonstrating how to seamlessly incorporate rationality principles (from economics and decision theory) into the learning process. By suitably tailoring the likelihood function, this framework enables the construction of preference learning models that encompass random utility models, limits of discernment, and scenarios with multiple conflicting utilities for both object- and label-preference. This tutorial builds upon established research while simultaneously introducing some novel GP-based models to address specific gaps in the existing literature.

Efficient Computation of Counterfactual Bounds

We assume to be given structural equations over discrete variables inducing a directed acyclic graph, namely, a structural causal model, together with data about its internal nodes. The question we want to answer is how we can compute bounds for partially identifiable counterfactual queries from such an input. We start by giving a map from structural casual models to credal networks. This allows us to compute exact counterfactual bounds via algorithms for credal nets on a subclass of structural causal models. Exact computation is going to be inefficient in general given that, as we show, causal inference is NP-hard even on polytrees. We target then approximate bounds via a causal EM scheme. We evaluate their accuracy by providing credible intervals on the quality of the approximation; we show through a synthetic benchmark that the EM scheme delivers accurate results in a fair number of runs. In the course of the discussion, we also point out what seems to be a neglected limitation to the trending idea that counterfactual bounds can be computed without knowledge of the structural equations. We also present a real case study on palliative care to show how our algorithms can readily be used for practical purposes.

Learning Choice Functions with Gaussian Processes

In consumer theory, ranking available objects by means of preference relations yields the most common description of individual choices. However, preference-based models assume that individuals: (1) give their preferences only between pairs of objects; (2) are always able to pick the best preferred object. In many situations, they may be instead choosing out of a set with more than two elements and, because of lack of information and/or incomparability (objects with contradictory characteristics), they may not able to select a single most preferred object. To address these situations, we need a choice-model which allows an individual to express a set-valued choice. Choice functions provide such a mathematical framework. We propose a Gaussian Process model to learn choice functions from choice-data. The proposed model assumes a multiple utility representation of a choice function based on the concept of Pareto rationalization, and derives a strategy to learn both the number and the values of these latent multiple utilities. Simulation experiments demonstrate that the proposed model outperforms the state-of-the-art methods.

Probabilistic reconciliation of forecasts via importance sampling

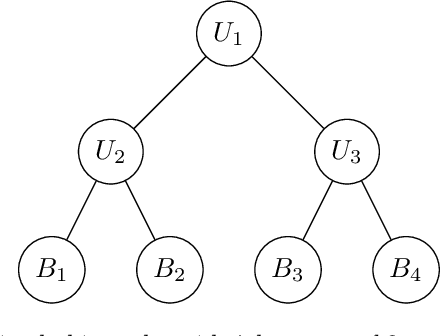
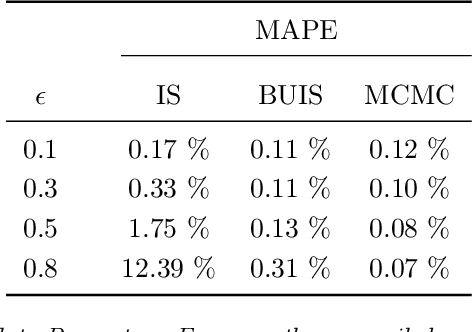
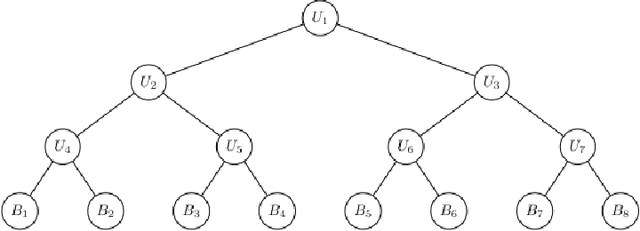
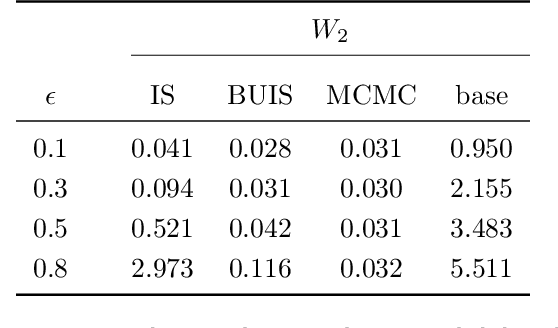
Hierarchical time series are common in several applied fields. Forecasts are required to be coherent, that is, to satisfy the constraints given by the hierarchy. The most popular technique to enforce coherence is called reconciliation, which adjusts the base forecasts computed for each time series. However, recent works on probabilistic reconciliation present several limitations. In this paper, we propose a new approach based on conditioning to reconcile any type of forecast distribution. We then introduce a new algorithm, called Bottom-Up Importance Sampling, to efficiently sample from the reconciled distribution. It can be used for any base forecast distribution: discrete, continuous, or even in the form of samples. The method was tested on several temporal hierarchies showing that our reconciliation effectively improves the quality of probabilistic forecasts. Moreover, our algorithm is up to 3 orders of magnitude faster than vanilla MCMC methods.

Bounding Counterfactuals under Selection Bias

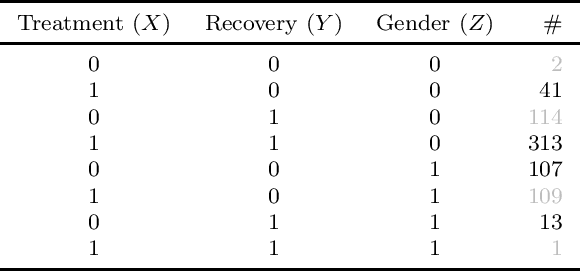
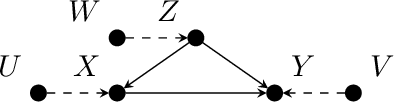
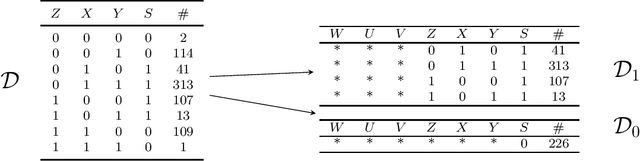
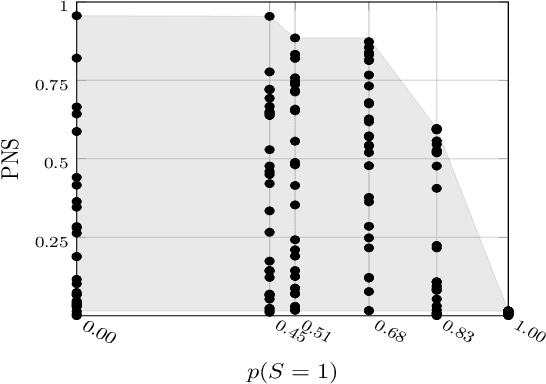
Causal analysis may be affected by selection bias, which is defined as the systematic exclusion of data from a certain subpopulation. Previous work in this area focused on the derivation of identifiability conditions. We propose instead a first algorithm to address both identifiable and unidentifiable queries. We prove that, in spite of the missingness induced by the selection bias, the likelihood of the available data is unimodal. This enables us to use the causal expectation-maximisation scheme to obtain the values of causal queries in the identifiable case, and to compute bounds otherwise. Experiments demonstrate the approach to be practically viable. Theoretical convergence characterisations are provided.

Probabilistic Reconciliation of Count Time Series

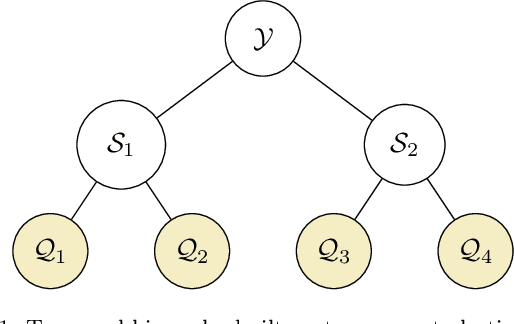
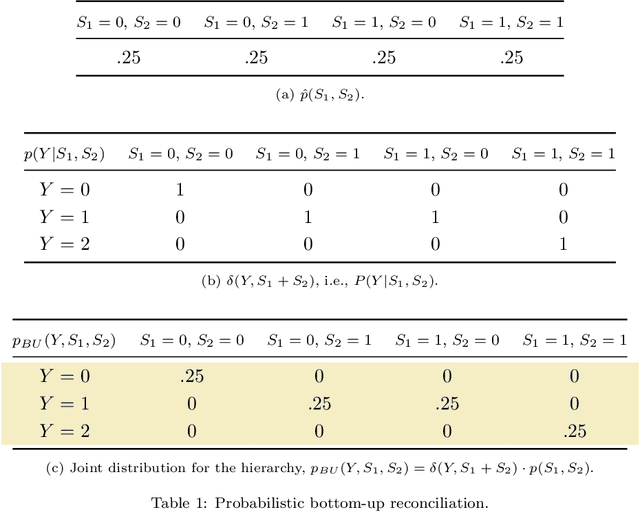
We propose a principled method for the reconciliation of any probabilistic base forecasts. We show how probabilistic reconciliation can be obtained by merging, via Bayes' rule, the information contained in the base forecast for the bottom and the upper time series. We illustrate our method on a toy hierarchy, showing how our framework allows the probabilistic reconciliation of any base forecast. We perform experiment in the reconciliation of temporal hierarchies of count time series, obtaining major improvements compared to probabilistic reconciliation based on the Gaussian or the truncated Gaussian distribution.

Correlated Product of Experts for Sparse Gaussian Process Regression

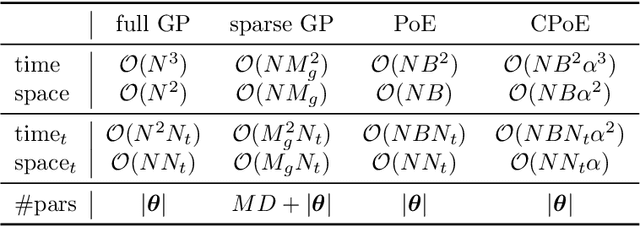
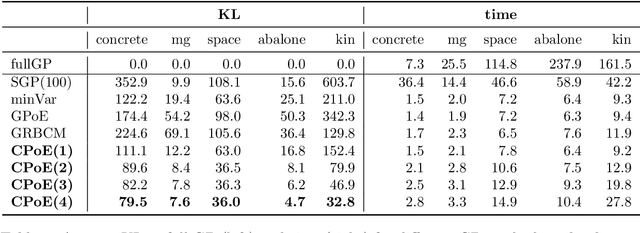
Gaussian processes (GPs) are an important tool in machine learning and statistics with applications ranging from social and natural science through engineering. They constitute a powerful kernelized non-parametric method with well-calibrated uncertainty estimates, however, off-the-shelf GP inference procedures are limited to datasets with several thousand data points because of their cubic computational complexity. For this reason, many sparse GPs techniques have been developed over the past years. In this paper, we focus on GP regression tasks and propose a new approach based on aggregating predictions from several local and correlated experts. Thereby, the degree of correlation between the experts can vary between independent up to fully correlated experts. The individual predictions of the experts are aggregated taking into account their correlation resulting in consistent uncertainty estimates. Our method recovers independent Product of Experts, sparse GP and full GP in the limiting cases. The presented framework can deal with a general kernel function and multiple variables, and has a time and space complexity which is linear in the number of experts and data samples, which makes our approach highly scalable. We demonstrate superior performance, in a time vs. accuracy sense, of our proposed method against state-of-the-art GP approximation methods for synthetic as well as several real-world datasets with deterministic and stochastic optimization.

Choice functions based multi-objective Bayesian optimisation

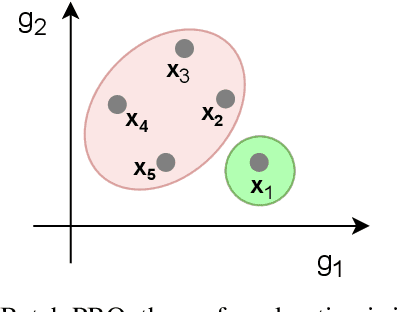
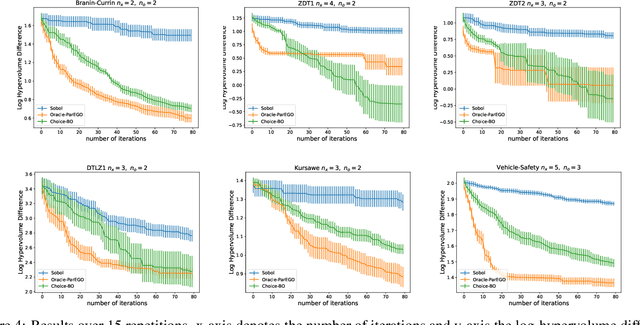
In this work we introduce a new framework for multi-objective Bayesian optimisation where the multi-objective functions can only be accessed via choice judgements, such as ``I pick options A,B,C among this set of five options A,B,C,D,E''. The fact that the option D is rejected means that there is at least one option among the selected ones A,B,C that I strictly prefer over D (but I do not have to specify which one). We assume that there is a latent vector function f for some dimension $n_e$ which embeds the options into the real vector space of dimension n, so that the choice set can be represented through a Pareto set of non-dominated options. By placing a Gaussian process prior on f and deriving a novel likelihood model for choice data, we propose a Bayesian framework for choice functions learning. We then apply this surrogate model to solve a novel multi-objective Bayesian optimisation from choice data problem.

A unified framework for closed-form nonparametric regression, classification, preference and mixed problems with Skew Gaussian Processes

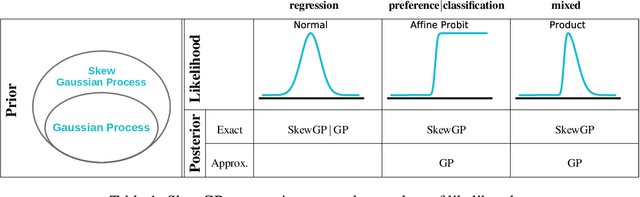
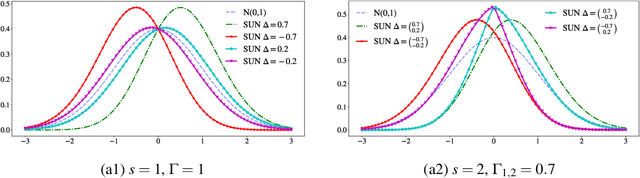
Skew-Gaussian processes (SkewGPs) extend the multivariate Unified Skew-Normal distributions over finite dimensional vectors to distribution over functions. SkewGPs are more general and flexible than Gaussian processes, as SkewGPs may also represent asymmetric distributions. In a recent contribution we showed that SkewGP and probit likelihood are conjugate, which allows us to compute the exact posterior for non-parametric binary classification and preference learning. In this paper, we generalize previous results and we prove that SkewGP is conjugate with both the normal and affine probit likelihood, and more in general, with their product. This allows us to (i) handle classification, preference, numeric and ordinal regression, and mixed problems in a unified framework; (ii) derive closed-form expression for the corresponding posterior distributions. We show empirically that the proposed framework based on SkewGP provides better performance than Gaussian processes in active learning and Bayesian (constrained) optimization.