Probabilistic reconciliation of forecasts via importance sampling
Paper and Code
Oct 05, 2022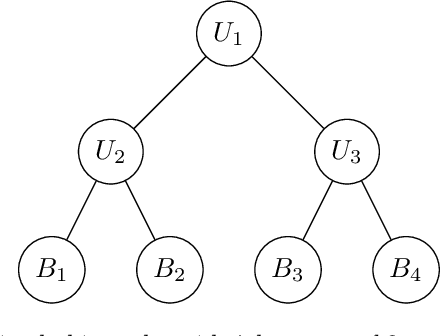
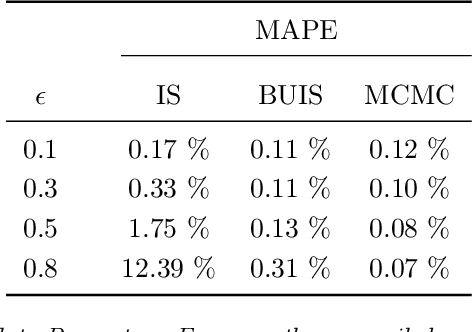
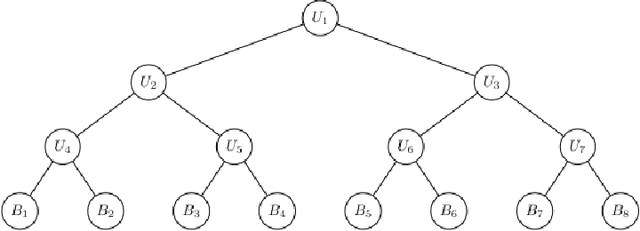
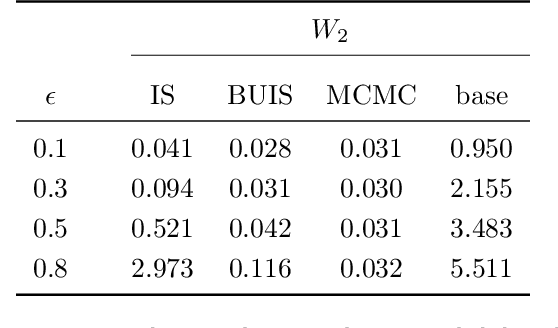
Hierarchical time series are common in several applied fields. Forecasts are required to be coherent, that is, to satisfy the constraints given by the hierarchy. The most popular technique to enforce coherence is called reconciliation, which adjusts the base forecasts computed for each time series. However, recent works on probabilistic reconciliation present several limitations. In this paper, we propose a new approach based on conditioning to reconcile any type of forecast distribution. We then introduce a new algorithm, called Bottom-Up Importance Sampling, to efficiently sample from the reconciled distribution. It can be used for any base forecast distribution: discrete, continuous, or even in the form of samples. The method was tested on several temporal hierarchies showing that our reconciliation effectively improves the quality of probabilistic forecasts. Moreover, our algorithm is up to 3 orders of magnitude faster than vanilla MCMC methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge