Forecasting intermittent time series with Gaussian Processes and Tweedie likelihood

We introduce the use of Gaussian Processes (GPs) for the probabilistic forecasting of intermittent time series. The model is trained in a Bayesian framework that accounts for the uncertainty about the latent function and marginalizes it out when making predictions. We couple the latent GP variable with two types of forecast distributions: the negative binomial (NegBinGP) and the Tweedie distribution (TweedieGP). While the negative binomial has already been used in forecasting intermittent time series, this is the first time in which a fully parameterized Tweedie density is used for intermittent time series. We properly evaluate the Tweedie density, which is both zero-inflated and heavy tailed, avoiding simplifying assumptions made in existing models. We test our models on thousands of intermittent count time series. Results show that our models provide consistently better probabilistic forecasts than the competitors. In particular, TweedieGP obtains the best estimates of the highest quantiles, thus showing that it is more flexible than NegBinGP.

Probabilistic reconciliation of forecasts via importance sampling

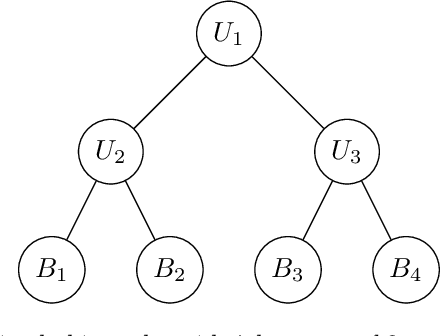
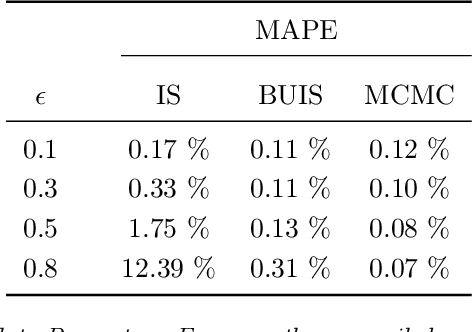
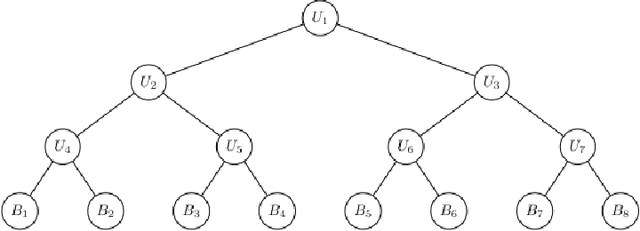
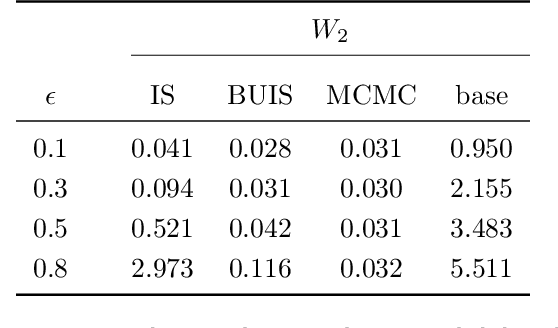
Hierarchical time series are common in several applied fields. Forecasts are required to be coherent, that is, to satisfy the constraints given by the hierarchy. The most popular technique to enforce coherence is called reconciliation, which adjusts the base forecasts computed for each time series. However, recent works on probabilistic reconciliation present several limitations. In this paper, we propose a new approach based on conditioning to reconcile any type of forecast distribution. We then introduce a new algorithm, called Bottom-Up Importance Sampling, to efficiently sample from the reconciled distribution. It can be used for any base forecast distribution: discrete, continuous, or even in the form of samples. The method was tested on several temporal hierarchies showing that our reconciliation effectively improves the quality of probabilistic forecasts. Moreover, our algorithm is up to 3 orders of magnitude faster than vanilla MCMC methods.

Probabilistic Reconciliation of Count Time Series

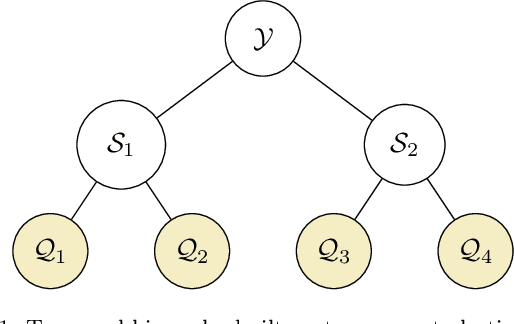
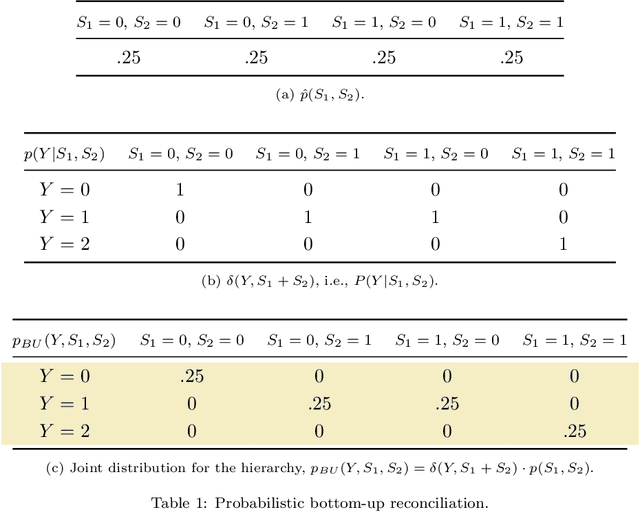
We propose a principled method for the reconciliation of any probabilistic base forecasts. We show how probabilistic reconciliation can be obtained by merging, via Bayes' rule, the information contained in the base forecast for the bottom and the upper time series. We illustrate our method on a toy hierarchy, showing how our framework allows the probabilistic reconciliation of any base forecast. We perform experiment in the reconciliation of temporal hierarchies of count time series, obtaining major improvements compared to probabilistic reconciliation based on the Gaussian or the truncated Gaussian distribution.

Automatic Forecasting using Gaussian Processes

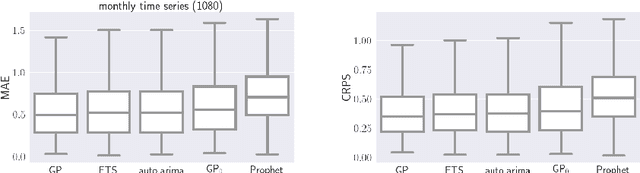
Automatic forecasting is the task of receiving a time series and returning a forecast for the next time steps without any human intervention. We propose an approach for automatic forecasting based on Gaussian Processes (GPs). So far, the main limits of GPs on this task have been the lack of a criterion for the selection of the kernel and the long times required for training different competing kernels. We design a fixed additive kernel, which contains the components needed to model most time series. During training the unnecessary components are made irrelevant by automatic relevance determination. We assign priors to each hyperparameter. We design the priors by analyzing a separate set of time series through a hierarchical GP. The resulting model performs very well on different types of time series, being competitive or outperforming the state-of-the-art approaches.Thanks to the priors, we reliably estimate the parameters with a single restart; this speedup makes the model efficient to train and suitable for processing a large number of time series.

Structure Learning from Related Data Sets with a Hierarchical Bayesian Score

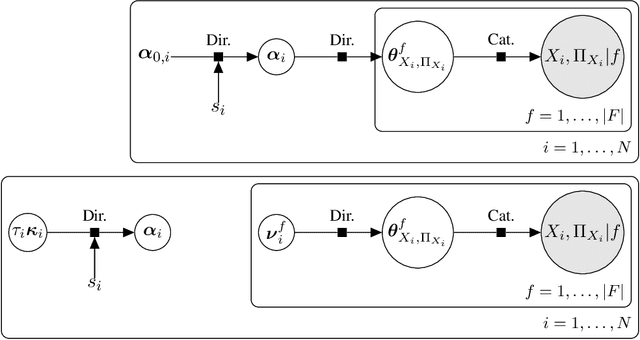
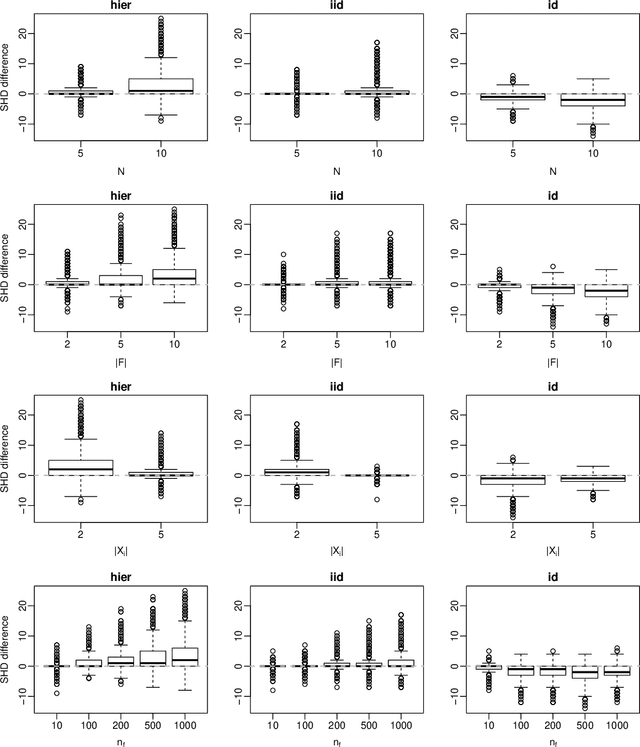
Score functions for learning the structure of Bayesian networks in the literature assume that data are a homogeneous set of observations; whereas it is often the case that they comprise different related, but not homogeneous, data sets collected in different ways. In this paper we propose a new Bayesian Dirichlet score, which we call Bayesian Hierarchical Dirichlet (BHD). The proposed score is based on a hierarchical model that pools information across data sets to learn a single encompassing network structure, while taking into account the differences in their probabilistic structures. We derive a closed-form expression for BHD using a variational approximation of the marginal likelihood and we study its performance using simulated data. We find that, when data comprise multiple related data sets, BHD outperforms the Bayesian Dirichlet equivalent uniform (BDeu) score in terms of reconstruction accuracy as measured by the Structural Hamming distance, and that it is as accurate as BDeu when data are homogeneous. Moreover, the estimated networks are sparser and therefore more interpretable than those obtained with BDeu, thanks to a lower number of false positive arcs.

Efficient Learning of Bounded-Treewidth Bayesian Networks from Complete and Incomplete Data Sets

Learning a Bayesian networks with bounded treewidth is important for reducing the complexity of the inferences. We present a novel anytime algorithm (k-MAX) method for this task, which scales up to thousands of variables. Through extensive experiments we show that it consistently yields higher-scoring structures than its competitors on complete data sets. We then consider the problem of structure learning from incomplete data sets. This can be addressed by structural EM, which however is computationally very demanding. We thus adopt the novel k-MAX algorithm in the maximization step of structural EM, obtaining an efficient computation of the expected sufficient statistics. We test the resulting structural EM method on the task of imputing missing data, comparing it against the state-of-the-art approach based on random forests. Our approach achieves the same imputation accuracy of the competitors, but in about one tenth of the time. Furthermore we show that it has worst-case complexity linear in the input size, and that it is easily parallelizable.

Entropy-based Pruning for Learning Bayesian Networks using BIC

For decomposable score-based structure learning of Bayesian networks, existing approaches first compute a collection of candidate parent sets for each variable and then optimize over this collection by choosing one parent set for each variable without creating directed cycles while maximizing the total score. We target the task of constructing the collection of candidate parent sets when the score of choice is the Bayesian Information Criterion (BIC). We provide new non-trivial results that can be used to prune the search space of candidate parent sets of each node. We analyze how these new results relate to previous ideas in the literature both theoretically and empirically. We show in experiments with UCI data sets that gains can be significant. Since the new pruning rules are easy to implement and have low computational costs, they can be promptly integrated into all state-of-the-art methods for structure learning of Bayesian networks.

Time for a change: a tutorial for comparing multiple classifiers through Bayesian analysis

The machine learning community adopted the use of null hypothesis significance testing (NHST) in order to ensure the statistical validity of results. Many scientific fields however realized the shortcomings of frequentist reasoning and in the most radical cases even banned its use in publications. We should do the same: just as we have embraced the Bayesian paradigm in the development of new machine learning methods, so we should also use it in the analysis of our own results. We argue for abandonment of NHST by exposing its fallacies and, more importantly, offer better - more sound and useful - alternatives for it.

Statistical comparison of classifiers through Bayesian hierarchical modelling

Usually one compares the accuracy of two competing classifiers via null hypothesis significance tests (nhst). Yet the nhst tests suffer from important shortcomings, which can be overcome by switching to Bayesian hypothesis testing. We propose a Bayesian hierarchical model which jointly analyzes the cross-validation results obtained by two classifiers on multiple data sets. It returns the posterior probability of the accuracies of the two classifiers being practically equivalent or significantly different. A further strength of the hierarchical model is that, by jointly analyzing the results obtained on all data sets, it reduces the estimation error compared to the usual approach of averaging the cross-validation results obtained on a given data set.

Learning Bounded Treewidth Bayesian Networks with Thousands of Variables

We present a method for learning treewidth-bounded Bayesian networks from data sets containing thousands of variables. Bounding the treewidth of a Bayesian greatly reduces the complexity of inferences. Yet, being a global property of the graph, it considerably increases the difficulty of the learning process. We propose a novel algorithm for this task, able to scale to large domains and large treewidths. Our novel approach consistently outperforms the state of the art on data sets with up to ten thousand variables.