Using Mixed-Effect Models to Learn Bayesian Networks from Related Data Sets

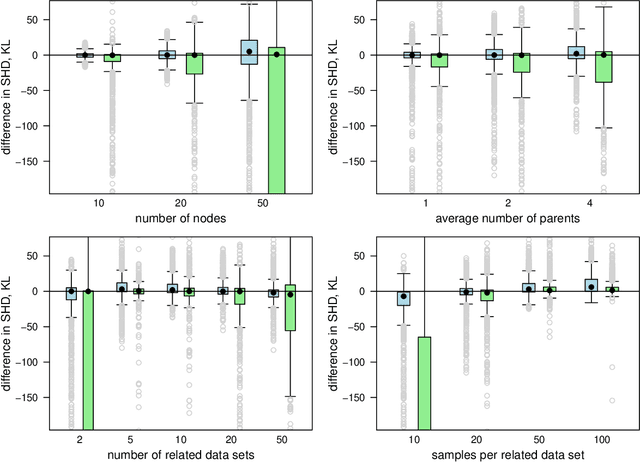
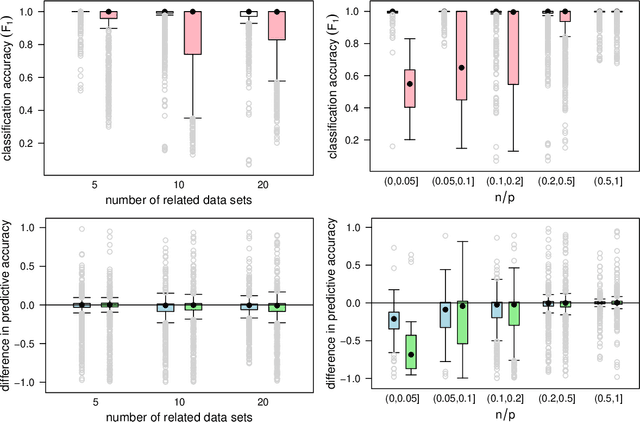
We commonly assume that data are a homogeneous set of observations when learning the structure of Bayesian networks. However, they often comprise different data sets that are related but not homogeneous because they have been collected in different ways or from different populations. In our previous work (Azzimonti, Corani and Scutari, 2021), we proposed a closed-form Bayesian Hierarchical Dirichlet score for discrete data that pools information across related data sets to learn a single encompassing network structure, while taking into account the differences in their probabilistic structures. In this paper, we provide an analogous solution for learning a Bayesian network from continuous data using mixed-effects models to pool information across the related data sets. We study its structural, parametric, predictive and classification accuracy and we show that it outperforms both conditional Gaussian Bayesian networks (that do not perform any pooling) and classical Gaussian Bayesian networks (that disregard the heterogeneous nature of the data). The improvement is marked for low sample sizes and for unbalanced data sets.

An exact kernel framework for spatio-temporal dynamics

A kernel-based framework for spatio-temporal data analysis is introduced that applies in situations when the underlying system dynamics are governed by a dynamic equation. The key ingredient is a representer theorem that involves time-dependent kernels. Such kernels occur commonly in the expansion of solutions of partial differential equations. The representer theorem is applied to find among all solutions of a dynamic equation the one that minimizes the error with given spatio-temporal samples. This is motivated by the fact that very often a differential equation is given a priori (e.g.~by the laws of physics) and a practitioner seeks the best solution that is compatible with her noisy measurements. Our guiding example is the Fokker-Planck equation, which describes the evolution of density in stochastic diffusion processes. A regression and density estimation framework is introduced for spatio-temporal modeling under Fokker-Planck dynamics with initial and boundary conditions.

Structure Learning from Related Data Sets with a Hierarchical Bayesian Score

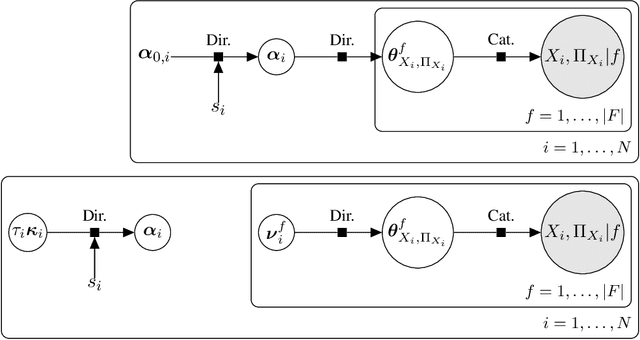
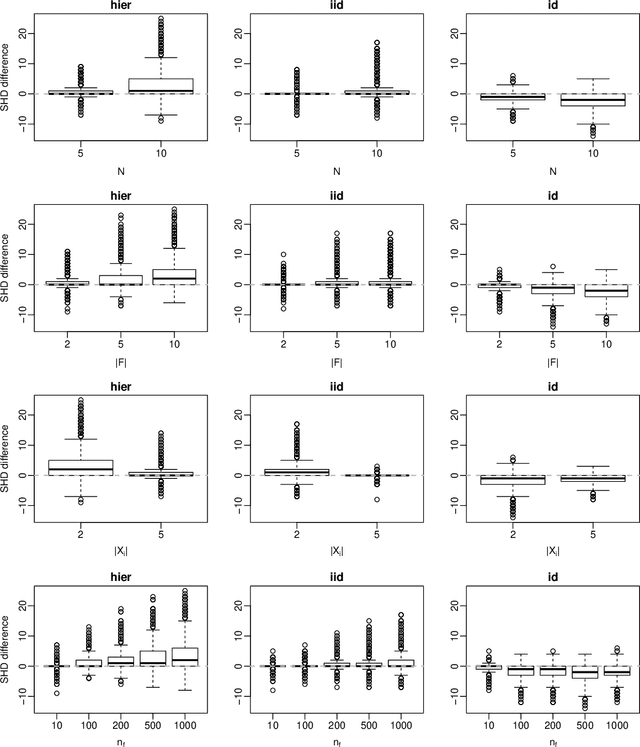
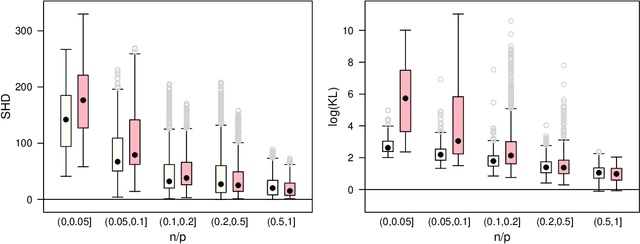
Score functions for learning the structure of Bayesian networks in the literature assume that data are a homogeneous set of observations; whereas it is often the case that they comprise different related, but not homogeneous, data sets collected in different ways. In this paper we propose a new Bayesian Dirichlet score, which we call Bayesian Hierarchical Dirichlet (BHD). The proposed score is based on a hierarchical model that pools information across data sets to learn a single encompassing network structure, while taking into account the differences in their probabilistic structures. We derive a closed-form expression for BHD using a variational approximation of the marginal likelihood and we study its performance using simulated data. We find that, when data comprise multiple related data sets, BHD outperforms the Bayesian Dirichlet equivalent uniform (BDeu) score in terms of reconstruction accuracy as measured by the Structural Hamming distance, and that it is as accurate as BDeu when data are homogeneous. Moreover, the estimated networks are sparser and therefore more interpretable than those obtained with BDeu, thanks to a lower number of false positive arcs.